Список правильных многомерных многогранников и соединений (Vhnvkt hjgfnl,ud] bukikbyjud] bukikijguuntkf n vky;nuyunw)

Примеры правильных многогранников

Правильные (2D) многоугольники
Выпуклые	Звёздчатые
{5}	{5/2}
Правильные 3D-многогранники
Выпуклые	Звёздчатые
{5,3}	{5/2,5}
Правильные 2D-замощения
Евклидовы	Гиперболические
{4,4}	{5,4}
Правильные 4D-многогранники
Выпуклые	Звёздчатые
{5,3,3}	{5/2,5,3}
Правильные 3D-замощения
Евклидовы	Гиперболические
{4,3,4}	{5,3,4}

Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.

Символ Шлефли описывает каждое правильное замощение n-сферы, евклидова и гиперболического пространства. Символ Шлефли описания n-мерного многогранника равным образом описывает мозаику (n-1)-сферы. Вдобавок, симметрия правильного многогранника или замощения выражается как группа Коксетера, которые Коксетер обозначал идентично символам Шлефли, за исключением разграничения квадратными скобками, и эта нотация называется нотацией Коксетера. Другой связанный символ — диаграмма Коксетера — Дынкина, которая представляет группу симметрии (без помеченных кружком узлов) и правильные многогранники или замощения с обведённым кружком первым узлом. Например, куб имеет символ Шлефли {4,3}, с его октаэдральной симметрией [4,3] или , представляется диаграммой Коксетера .

Правильные многогранники сгруппированы по размерности, а затем по форме — выпуклые, невыпуклые и бесконечные. Невыпуклые виды используют те же вершины, что и выпуклые, но имеют пересекающиеся фасеты (грани максимальной размерности = размерности пространства – 1). Бесконечные виды замощают евклидово пространство на единицу меньшей размерности.

Бесконечные формы можно расширить до замощения гиперболического пространства. Гиперболическое пространство подобно обычному пространству, но параллельные прямые с расстоянием расходятся. Это позволяет вершинным фигурам иметь отрицательные угловые дефекты. Например, в вершине может сходиться семь правильных треугольников, лежащих на плоскости. Это нельзя осуществить на обычной (евклидовой) плоскости, но можно сделать при некотором масштабе на гиперболической плоскости.

Многогранники, удовлетворяющие более общему определению и не имеющие простых символов Шлефли, включают правильные косые многогранники и бесконечноугольные правильные косые многогранники с неплоскими фасетами или вершинными фигурами.

Обзор

Таблица показывает сводку правильных многогранников по размерностям.

	Конечные			Евклидовы	Гиперболические			Соединения
Разм.	Выпук- лые	Звёзд- чатые	Косые	Выпук- лые	Компак- тные	Звёзд- чатые	Параком- пактные	Выпук- лые	Звёзд- чатые
1	1	0	0	1	0	0	0	0	0
2	∞	∞	∞	1	1	0	0	∞	∞
3	5	4	?	3	∞	∞	∞	5	0
4	6	10	?	1	4	0	11	26	20
5	3	0	?	3	5	4	2	0	0
6	3	0	?	1	0	0	5	0	0
7	3	0	?	1	0	0	0	3	0
8	3	0	?	1	0	0	0	6	0
9+	3	0	?	1	0	0	0	*	0

* 1, если размерность имеет вид 2^k − 1; 2, если размерность является степенью двойки; 0 в противном случае.

Не существует правильных звёздчатых замощений в евклидовом пространстве любой размерности.

Одномерное пространство

Диаграмма Коксетера — Дынкина представляет зеркальные "плоскости" как узлы, и помещает кружок вокруг узла, если точка не лежит на плоскости. Отрезок, { }, — это точка p и зеркальный образ точки p, а также отрезок между ними.

Одномерный многогранник (1-многогранник) — это замкнутый отрезок, ограниченный двумя конечными точками. 1-многогранник является правильным по определению и представляется символом Шлефли { } или диаграммой Коксетера с единственным помеченным кружком узлом, . Норман Джонсон дал им название дайтел и символ Шлефли { } .

Будучи тривиальным в качестве многогранника, дайтел возникает в качестве рёбер многоугольников и многогранников. Он используется в определении однородных призм (как в символе Шлефли { }×{p}) или в диаграмме Коксетера как прямое произведение отрезка и правильного многоугольника .

Двумерное пространство (многоугольники)

Двумерные многогранники называются многоугольниками. Правильные многоугольники имеют равные стороны и вписаны в окружность. Правильный p-угольник представляется символом Шлефли {p}.

Обычно только выпуклые многоугольники считаются правильными, но звёздчатые многоугольники наподобие пентаграммы можно также считать правильными. Они используют те же вершины, что и выпуклые формы, но соединение происходит другим путём, при котором окружность обходится более одного раза.

Звёздчатые многоугольники следует называть скорее невыпуклыми, чем вогнутыми, поскольку пересечение рёбер не образует новых вершин и все вершины находятся на окружности.

Выпуклые

Символ Шлефли {p} представляет правильный p-угольник.

Название	Треугольник (2-симплекс)	Квадрат (2-ортоплекс) (2-куб)	Пятиугольник	Шестиугольник	Семиугольник	Восьмиугольник
Шлефли	{3}	{4}	{5}	{6}	{7}	{8}
Симметрия	D3, [3]	D4, [4]	D5, [5]	D6, [6]	D7, [7]	D8, [8]
Коксетер
Рисунок
Название	Девятиугольник	Десятиугольник	Одиннадцатиугольник	Двенадцатиугольник	Тринадцатиугольник	Четырнадцатиугольник
Шлефли	{9}	{10}	{11}	{12}	{13}	{14}
Симметрия	D9, [9]	D10, [10]	D11, [11]	D12, [12]	D13, [13]	D14, [14]
Дынкин
Рисунок
Название	Пятнадцатиугольник	Шестнадцатиугольник	Семнадцатиугольник	Восемнадцатиугольник	Девятнадцатиугольник	Двадцатиугольник	...p-угольник
Шлефли	{15}	{16}	{17}	{18}	{19}	{20}	{p}
Симметрия	D15, [15]	D16, [16]	D17, [17]	D18, [18]	D19, [19]	D20, [20]	Dp, [p]
Дынкин
Рисунок

Сферические

Правильный двуугольник {2} можно считать вырожденным правильным многоугольником. Он может существовать как невырожденный в некоторых неевклидовых пространствах, таких как поверхность сферы или тора.

Название	Одноугольник	Двуугольник
Символ Шлефли	{1}	{2}
Симметрия	D1, [ ]	D2, [2]
Коксетер diagram	или
Рисунок

Звёзды

Существует бесконечно много правильных звёздчатых многогранников в двумерном пространстве (т.е. многоугольников), символы Шлефли которых являются рациональными числами {n/m}. Они называются звёздчатыми многоугольниками и имеют то же самое расположение вершин, что и у выпуклого многоугольника.

В общем случае для любого натурального числа n и для всех m, таких, что m < n/2 и m, n взаимно просты, существуют n-точечные правильные звёзды с символами Шлефли {n/m} (строго говоря, {n/m}={n/(n−m)}) .

Название	Пентаграмма	Гептаграммы		Октаграмма	Эннеаграммы		Декаграмма	...n-граммы
Шлефли	{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}	{10/3}	{p/q}
Симметрия	D5, [5]	D7, [7]		D8, [8]	D9, [9],		D10, [10]	Dp, [p]
Коксетер
Рисунок

Правильные звёздчатые многоугольники с числом сторон до 20

{11/2}	{11/3}	{11/4}	{11/5}	{12/5}	{13/2}	{13/3}	{13/4}	{13/5}	{13/6}
{14/3}	{14/5}	{15/2}	{15/4}	{15/7}	{16/3}	{16/5}	{16/7}
{17/2}	{17/3}	{17/4}	{17/5}	{17/6}	{17/7}	{17/8}	{18/5}	{18/7}
{19/2}	{19/3}	{19/4}	{19/5}	{19/6}	{19/7}	{19/8}	{19/9}	{20/3}	{20/7}	{20/9}

Пространственные многоугольники

В 3-мерном пространстве правильный пространственный многоугольник называется антипризматическим многоугольником и он имеет то же расположение вершин, что и у антипризмы, и его рёбра являются подмножеством рёбер антипризмы, соединяющие зигзагом вершины верхнего и нижнего многоугольников.

Пример правильного пространственного зигзаг-многоугольника

Шестиугольник	Восьмиугольник	Десятиугольник
D3d, [2+,6]	D4d, [2+,8]	D5d, [2+,10]
{3}#{ }	{4}#{ }	{5}#{ }	{5/2}#{ }	{5/3}#{ }

В 4-мерном пространстве правильный пространственный многоугольник может иметь вершины на торе Клиффорда и связан с вращением Клиффорда. В отличие от антипризматичных пространственных многоугольников, пространственные многоугольники двойного вращения могут иметь нечётное число сторон.

Их можно видеть в многоугольниках Петри выпуклых правильных четырёхмерных многогранников, видимые как правильные плоские многоугольники периметров проекций Коксетера:

Пятиугольник	Восьмиугольник	Двенадцатиугольник	Тридцатиугольник
Пятиячейник	Шестнадцатиячейник	Двадцатичетырёхъячейник	Шестисотячейник

Трёхмерное пространство (многогранники)

В трёхмерном пространстве правильный многогранник с символом Шлефли {p,q} и диаграммой Коксетера имеет правильные грани вида {p} и правильную вершинную фигуру {q}.

Вершинная фигура (многогранника) является многоугольником, получаемым соединением вершин, отстоящих на одно ребро от заданной вершины. Для правильных трёхмерных многогранников, эта вершинная фигура является всегда правильным (и планарным) многоугольником.

Существование правильного многогранника {p,q} ограничено неравенством, относящимся к угловому дефекту вершинной фигуры:

${\frac {1}{p}}+{\frac {1}{q}}>{\frac {1}{2}}$ : Многогранник (существует в евклидовом 3-мерном пространстве)

${\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{2}}$ : Евклидова плоская мозаика

${\frac {1}{p}}+{\frac {1}{q}}<{\frac {1}{2}}$ : Замощение гиперболической плоскости

Перенумеровав перестановки, мы найдём 5 выпуклых форм, 4 звёздчатые формы и 3 плоских замощения, все с многоугольниками {p} и {q} из списка: {3}, {4}, {5}, {5/2} и {6}.

Вдобавок к мозаикам евклидова пространства существует бесконечное количество правильных гиперболических мозаик.

Выпуклые

Пять выпуклых правильных многогранников называются платоновыми телами. Вершинная фигура указана вместе с числом вершин. Все эти многогранники имеют эйлерову характеристику (χ) 2.

Название	Шлефли {p,q}	Коксетер	Рисунок (прозрачный)	Рисунок (тело)	Рисунок (сфера)	Граней {p}	Рёбер	Вершин {q}	Симметрия	Двойственный
Тетраэдр (3-симплекс)	{3,3}					4 {3}	6	4 {3}	Td [3,3] (*332)	(самодвойственен)
Шестигранник Куб (3-куб)	{4,3}					6 {4}	12	8 {3}	Oh [4,3] (*432)	Октаэдр
Октаэдр (3-ортоплекс)	{3,4}					8 {3}	12	6 {4}	Oh [4,3] (*432)	Куб
Додекаэдр	{5,3}					12 {5}	30	20 {3}	Ih [5,3] (*532)	Икосаэдр
Икосаэдр	{3,5}					20 {3}	30	12 {5}	Ih [5,3] (*532)	Додекаэдр

Сферические

В сферической геометрии существуют правильные сферические многогранники (мозаики на cфере), которые в нормальном случае являются вырожденными многогранниками. Это осоэдры {2,n} и двойственные им диэдры {n,2}. Коксетер называет такие случаи "несобственными" замощениями .

Несколько первых примеров (n от 2 до 6) приведены ниже.

Осоэдры

Название	Шлефли {2,p}	Коксетер diagram	Рисунок (sphere)	Граней {2}π/p	Рёбер	Вершин {p}	Симметрия	Двойственный
Двуугольный осоэдр	{2,2}			2 {2}π/2	2	2 {2}π/2	D2h [2,2] (*222)	Самодвойственен
Треугольный осоэдр	{2,3}			3 {2}π/3	3	2 {3}	D3h [2,3] (*322)	Треугольный диэдр
Квадратный осоэдр	{2,4}			4 {2}π/4	4	2 {4}	D4h [2,4] (*422)	Квадратный диэдр
Пятиугольный осоэдр	{2,5}			5 {2}π/5	5	2 {5}	D5h [2,5] (*522)	Пятиугольный диэдр
Шестиугольный осоэдр	{2,6}			6 {2}π/6	6	2 {6}	D6h [2,6] (*622)	Шестиугольный диэдр

Диэдры

Название	Шлефли {p,2}	Диаграмма Коксетера	Рисунок (сфера)	Граней {p}	Рёбер	Вершин {2}	Симметрия	Двойственный
Двуугольный диэдр	{2,2}			2 {2}π/2	2	2 {2}π/2	D2h [2,2] (*222)	Самодвойственен
Треугольный диэдр	{3,2}			2 {3}	3	3 {2}π/3	D3h [3,2] (*322)	Треугольный осоэдр
Квадратный диэдр	{4,2}			2 {4}	4	4 {2}π/4	D4h [4,2] (*422)	Квадратный осоэдр
Пятиугольный диэдр	{5,2}			2 {5}	5	5 {2}π/5	D5h [5,2] (*522)	Пятиугольный осоэдр
Шестиугольный диэдр	{6,2}			2 {6}	6	6 {2}π/6	D6h [6,2] (*622)	Шестиугольный осоэдр

Звёздчатые диэдры и осоэдры также существуют, такие как {5/2,2} и {2,5/2}.

Звёзды

Правильные звёздчатые многогранники называются телами Кеплера — Пуансо и их существует четыре. Они основываются на расположении вершин додекаэдра {5,3} и икосаэдра {3,5}:

Как cферические мозаики эти звёздчатые формы перекрывают сферу несколько раз, что называется их плотностью. Для этих форм плотность равна 3 или 7. Рисунки мозаик показывают грани отдельных сферических многоугольников жёлтым цветом.

Название	Рисунок (прозрачный)	Рисунок (непрозрачный)	Рисунок (сферический)	Диаграмма образования звёздчатой формы	Шлефли {p,q} и Коксетер	Граней {p}	Рёбер	Вершин {q} Фигура	χ	Плот- ность	Симметрия	Двойственный
Малый звёздчатый додекаэдр					{5/2,5}	12 {5/2}	30	12 {5}	−6	3	Ih [5,3] (*532)	Большой додекаэдр
Большой додекаэдр					{5,5/2}	12 {5}	30	12 {5/2}	−6	3	Ih [5,3] (*532)	Малый звёздчатый додекаэдр
Большой звёздчатый додекаэдр					{5/2,3}	12 {5/2}	30	20 {3}	2	7	Ih [5,3] (*532)	Большой икосаэдр
Большой икосаэдр					{3,5/2}	20 {3}	30	12 {5/2}	2	7	Ih [5,3] (*532)	Большой звёздчатый додекаэдр

Косые многогранники

Правильный косой многогранник является обобщением множества правильных многогранников, в котором допускается непланарность вершинных фигур.

Для 4-мерных косых многогранников Коксетер предложил модифицированный символ Шлефли {l,m|n}, имеющих вершинную фигуру {l,m}, m l-угольников вокруг вершины с n-угольными дырами. Их вершинные фигуры являются пространственными многоугольниками, представляющими зигзаги между двумя плоскостями.

Для правильных косых многогранников, представленных символом {l,m|n}, выполняется равенство:

2*sin(π/l)*sin(π/m)=cos(π/n)

Четыре из них можно видеть в 4-мерном пространстве как множество граней четырёх правильных четырёхмерных многогранников, имеющих одно и то же расположение вершин и расположение рёбер:

{4, 6 | 3}	{6, 4 | 3}	{4, 8 | 3}	{8, 4 | 3}

Четырёхмерное пространство

Правильные 4-мерные многогранники с символом Шлефли $\{p,q,r\}$ имеют ячейки вида $\{p,q\}$, грани вида $\{p\}$, рёберные фигуры $\{r\}$ и вершинные фигуры $\{q,r\}$.

• Вершинная фигура (4-мерного многогранника) является (3-мерным) многогранником, образованным соседними к данной вершине вершинами многогранника. Для правильных четырёхмерных многогранников эта вершинная фигура является правильным (3-мерным) многогранником.
• Рёберной фигурой является многоугольник, образованный прилегающими к ребру гранями. Для правильных четырёхмерных многогранников рёберной фигурой всегда будет правильный многоугольник.

Существование правильных четырёхмерных многогранников $\{p,q,r\}$ ограничено существованием правильного многогранника $\{p,q\},\{q,r\}$. Для 4-мерных многогранников предлагается использовать название "полихор"

Каждый вид может существовать в пространстве, зависящем от следующего выражения:

$\sin \left({\frac {\pi }{p}}\right)\sin \left({\frac {\pi }{r}}\right)-\cos \left({\frac {\pi }{q}}\right)$

$>0$ : Гиперсферические 3-мерные соты или 4-мерные многогранники

$=0$ : евклидовы 3-мерные соты

$<0$ : Гиперболические 3-мерные соты

Эти ограничения допустимы для 21 форм — 6 форм выпуклы, 10 не выпуклы, одна является евклидовыми 3-мерными сотами и 4 являются гиперболическими сотами.

Эйлерова характеристика $\chi$ четырёхмерного многогранника вычисляется по формуле $\chi =V+F-E-C$ и равна нулю для всех видов.

Выпуклые

6 выпуклых правильных четырёхмерных многогранников показаны в таблице ниже. Все эти многогранники имеют эйлерову характеристику (χ) 0.

Название	Шлефли {p,q,r}	Коксетер	Ячейки {p,q}	Граней {p}	Рёбер {r}	Вершин {q,r}	Двойственный {r,q,p}
Пятиячейник (4-симплекс)	{3,3,3}		5 {3,3}	10 {3}	10 {3}	5 {3,3}	(самодвойственен)
Тессеракт (4-куб)	{4,3,3}		8 {4,3}	24 {4}	32 {3}	16 {3,3}	Шестнадцатиячейник
Шестнадцатиячейник (4-ортоплекс)	{3,3,4}		16 {3,3}	32 {3}	24 {4}	8 {3,4}	Тессеракт
Двадцатичетырёхъячейник	{3,4,3}		24 {3,4}	96 {3}	96 {3}	24 {4,3}	(самодвойственен)
Стодвадцатиячейник	{5,3,3}		120 {5,3}	720 {5}	1200 {3}	600 {3,3}	Шестисотъячейник
Шестисотъячейник	{3,3,5}		600 {3,3}	1200 {3}	720 {5}	120 {3,5}	Стодвадцатиячейник

Пятиячейник	Тессеракт	Шестнадцати- ячейник	Двадцати- четырёхъячейник	Стодвадцати- ячейник	Шестисотъячейник
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}
Каркас (Многоугольник Петри) в косой ортогональной проекции
Ортогональная проекция
Тетраэдральная оболочка (центрировано по ячейке/вершине)	Кубическая оболочка (центрировано по ячейке)	Кубическая оболочка (центрировано по ячейке)	Кубооктаэдральная оболочка (центрировано по ячейке)	Усечённая ромботриаконта- эдральная оболочка (центрировано по ячейке)	Пентакиикоси- додекаэдральная оболочка (центрировано по вершине)
Диаграммы Шлегеля (перспективная проекция)
(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по ячейке)	(центрировано по вершине)
Каркас стереографической проекции (гиперсферический)

Сферические

4-мерные диэдры и осоэдры существуют как правильные замощения 3-сферы.

Правильные 4-мерные диэдры (2 фасеты = 3-мерные грани) включают: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2} и их двойственные 4-мерные осоэдры (2 вершины): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}, {2,2,p}. Многогранники вида {2,p,2} являются одновременно 4-мерными диэдрами и осоэдрами. Существуют также формы {p,2,q}, которые имеют диэдральные ячейки и осоэдральные вершинные фигуры.

Правильные 4-мерные осоэдры как соты на 3-сфере

Шлефли {2,p,q}	Коксетер	Ячейки {2,p}π/q	Граней {2}π/p,π/q	Рёбер	Вершин	Вершинная фигура {p,q}	Симметрия	Двойственный
{2,3,3}		4 {2,3}π/3	6 {2}π/3,π/3	4	2	{3,3}	[2,3,3]	{3,3,2}
{2,4,3}		6 {2,4}π/3	12 {2}π/4,π/3	8	2	{4,3}	[2,4,3]	{3,4,2}
{2,3,4}		8 {2,3}π/4	12 {2}π/3,π/4	6	2	{3,4}	[2,4,3]	{4,3,2}
{2,5,3}		12 {2,5}π/3	30 {2}π/5,π/3	20	2	{5,3}	[2,5,3]	{3,5,2}
{2,3,5}		20 {2,3}π/5	30 {2}π/3,π/5	12	2	{3,5}	[2,5,3]	{5,3,2}

Звёзды

Существует десять правильных 4-мерных звёздчатых многогранника, которые называются многогранниками Шлефли—Гесса. Их вершины располагаются на выпуклом стодвадцатиячейнике {5,3,3} и шестисотъячейнике {3,3,5}.

Людвиг Шлефли нашёл четыре из них и отбросил остальные шесть, поскольку не позволял нарушение эйлеровой характеристики на ячейках или вершинных фигурах (F+V−E=2). Эдмунд Гесс (Edmund Hess, 1843–1903) завершил список в своей книге Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder ([3], 1883) (Введение в учение о замощении сферы с учётом теории равногранных и равноугольных многогранников) .

Существует 4 расположения рёбер и 7 расположений граней в этих 10 правильных звёздчатых 4-мерных многогранниках, показанные как ортогональные проекции:

Название	Каркас	Тело	Шлефли {p, q, r} Коксетер	Ячеек {p, q}	Граней {p}	Рёбер {r}	Вершин {q, r}	Плот- ность	χ	Группа симметрии	Двойственный {r, q,p}
Икосаэдральный 120-ячейник (огранённый Шестисотячейник)			{3,5,5/2}	120 {3,5}	1200 {3}	720 {5/2}	120 {5,5/2}	4	480	H4 [5,3,3]	Малый звёздчатый 120-ячейник
Малый звёздчатый 120-ячейник			{5/2,5,3}	120 {5/2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	−480	H4 [5,3,3]	Икосаэдральный 120-ячейник
Большой 120-ячейник			{5,5/2,5}	120 {5,5/2}	720 {5}	720 {5}	120 {5/2,5}	6	0	H4 [5,3,3]	Самодвойственный
Великий 120-ячейник			{5,3,5/2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5/2}	20	0	H4 [5,3,3]	Большой звёздчатый 120-ячейник
Большой звёздчатый 120-ячейник			{5/2,3,5}	120 {5/2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0	H4 [5,3,3]	Великий 120-ячейник
Великий звёздчатый 120-ячейник			{5/2,5,5/2}	120 {5/2,5}	720 {5/2}	720 {5/2}	120 {5,5/2}	66	0	H4 [5,3,3]	Самодвойственный
Большой великий 120-ячейник			{5,5/2,3}	120 {5,5/2}	720 {5}	1200 {3}	120 {5/2,3}	76	−480	H4 [5,3,3]	Большой икосаэдральный 120-ячейник
Большой икосаэдральный 120-ячейник (большой огранёный 600-ячейник)			{3,5/2,5}	120 {3,5/2}	1200 {3}	720 {5}	120 {5/2,5}	76	480	H4 [5,3,3]	Великий большой 120-ячейник
Великий 600-ячейник			{3,3,5/2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5/2}	191	0	H4 [5,3,3]	Великий большой звёздчатый 120-ячейник
Большой великий 120-ячейник			{5/2,3,3}	120 {5/2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0	H4 [5,3,3]	Великий 600-ячейник

Существует 4 несостоявшихся правильных звёздчатых перестановок многогранников: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. Их ячейки и вершинные фигуры существует, но они не покрывают гиперсферу конечным числом представлений.

Размерность пять и выше

В пятимерном пространстве правильные многогранники можно обозначить как $\{p,q,r,s\}$, где $\{p,q,r\}$ является типом 4-грани, $\{p,q\}$ является типом ячейки, $\{p\}$ является типом 2-грани, $\{s\}$ является фигурой грани, $\{r,s\}$ является рёберной фигурой, а $\{q,r,s\}$ является вершинной фигурой.

Вершинная фигура (5-мерного многогранника) является 4-мерным многогранником, образованным вершинами, соседними с данной вершиной.

Рёберная фигура (5-мерного многогранника) является многогранником, образованным гранями вокруг каждого ребра.

Фигура грани (5-мерного многогранника) является многогранником, образованным ячейками вокруг каждой грани.

Правильный 5-мерный многогранник $\{p,q,r,s\}$ существует, только если $\{p,q,r\}$ и $\{q,r,s\}$ являются правильными четырёхмерными многогранниками.

В зависимости от значения

${\frac {\cos ^{2}\left({\frac {\pi }{q}}\right)}{\sin ^{2}\left({\frac {\pi }{p}}\right)}}+{\frac {\cos ^{2}\left({\frac {\pi }{r}}\right)}{\sin ^{2}\left({\frac {\pi }{s}}\right)}}$

получим тип пространства

$<1$: Сферическое 4-мерное замощение или 5-мерный многогранник

$=1$: евклидово 4-мерное замощение

$>1$: Гиперболическое 4-мерное замощение

Из этих ограничений получаем 3 выпуклых многогранника, нуль невыпуклых многогранников, 3 4-мерных замощения и 5 гиперболических 4-мерных замощений. Не существует невыпуклых правильных многогранников в пятимерном пространстве и выше.

Выпуклые

В размерностях 5 и выше существует только три вида выпуклых правильных многогранников .

Название	Символ Шлефли {p1,...,pn−1}	Коксетер	k-граней	Тип фасеты	Вершинная фигура	Двойственный
n-симплекс	{3n−1}	...	${{n+1} \choose {k+1}}$	{3n−2}	{3n−2}	Самодвойственен
n-куб	{4,3n−2}	...	$2^{n-k}{n \choose k}$	{4,3n−3}	{3n−2}	n-ортоплекс
n-ортоплекс	{3n−2,4}	...	$2^{k+1}{n \choose {k+1}}$	{3n−2}	{3n−3,4}	n-куб

Существуют также несобственные случаи, в которых некоторые числа в символе Шлефли равны 2. Например, {p,q,r,...2} является несобственным правильным сферическим многогранником в случае, если {p,q,r...} является правильным сферическим многогранником, и {2,...p,q,r} является несобственным правильным сферическим многогранником, когда {...p,q,r} является правильным сферическим многогранником. Такие многогранники можно использовать как фасеты, дающие формы вида {p,q,...2...y,z}.

Пятимерные пространства

Название	Символ Шлефли {p,q,r,s} Коксетер	Число фасет (четырёхмерных граней) {p,q,r}	Ячеек (трёхмерных граней) {p,q}	Граней (двумерных) {p}	Рёбер	Вершин	Фигура при грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}
Гексатерон	{3,3,3,3}	6 {3,3,3}	15 {3,3}	20 {3}	15	6	{3}	{3,3}	{3,3,3}
Пентеракт	{4,3,3,3}	10 {4,3,3}	40 {4,3}	80 {4}	80	32	{3}	{3,3}	{3,3,3}
5-ортоплекс	{3,3,3,4}	32 {3,3,3}	80 {3,3}	80 {3}	40	10	{4}	{3,4}	{3,3,4}

Гексатерон

Пентеракт

5-ортоплекс

Шестимерное пространство

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	χ
6-симплекс	{3,3,3,3,3}	7	21	35	35	21	7	0
Хексеракт	{4,3,3,3,3}	64	192	240	160	60	12	0
6-ортоплекс	{3,3,3,3,4}	12	60	160	240	192	64	0

6-мерный симплекс

Хексеракт

6-мерный ортоплекс

Семимерное пространство

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	χ
7-симплекс	{3,3,3,3,3,3}	8	28	56	70	56	28	8	2
Хептеракт	{4,3,3,3,3,3}	128	448	672	560	280	84	14	2
7-ортоплекс	{3,3,3,3,3,4}	14	84	280	560	672	448	128	2

7-симплекс

Хептеракт

7-ортоплекс

Восьмимерное пространство

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	7D-граней	χ
8-симплекс	{3,3,3,3,3,3,3}	9	36	84	126	126	84	36	9	0
Октеракт	{4,3,3,3,3,3,3}	256	1024	1792	1792	1120	448	112	16	0
8-ортоплекс	{3,3,3,3,3,3,4}	16	112	448	1120	1792	1792	1024	256	0

8-симплекс

Октеракт

8-ортоплекс

Девятимерное пространство

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	7D-граней	8D-граней	χ
9-симплекс	{38}	10	45	120	210	252	210	120	45	10	2
Энтенеракт	{4,37}	512	2304	4608	5376	4032	2016	672	144	18	2
9-ортоплекс	{37,4}	18	144	672	2016	4032	5376	4608	2304	512	2

9-симплекс

Энтенеракт

9-ортоплекс

Десятимерное пространство

Название	Шлефли	Вершин	Рёбер	Граней (2D)	Ячеек (3D)	4D-граней	5D-граней	6D-граней	7D-граней	8D-граней	9D-граней	χ
10-симплекс	{39}	11	55	165	330	462	462	330	165	55	11	0
Декеракт	{4,38}	1024	5120	11520	15360	13440	8064	3360	960	180	20	0
10-ортоплекс	{38,4}	20	180	960	3360	8064	13440	15360	11520	5120	1024	0

10-симплекс

Декеракт

10-ортоплекс

...

Невыпуклые

Не существует невыпуклых правильных многогранников в размерностях 5 и выше.

Правильные проективные многогранники

Проективный правильный (n+1)-многогранник существует, если исходное правильное n-сферическое замощение {p,q,...} центрально симметрично. Такие многогранники называются полу-{p,q,...}, и содержат вполовину меньше элементов. Коксетер даёт им символ {p,q,...}/2, в то время как Макмуллен пишет {p,q,...}_h/2, где h — число Кокстера.

Правильные многоугольники с чётным числом сторон имеют полу-2n-угольные проективные многоугольники, {2p}/2.

Существует 4 правильных проективных многогранника, соответствующих 4 из 5 платоновых тел.

Полукуб и полуоктаэдр обобщаются в полу-n-кубы и полу-n-ортоплексы в любой размерности.

Правильные проективные многогранники в трёхмерном пространстве

3-dimensional regular hemi-polytopes

Название	Коксетер McMullen	Image	Faces	Edges	Vertices	χ
Полукуб	{4,3}/2 {4,3}3		3	6	4	1
Полуоктаэдр	{3,4}/2 {3,4}3		4	6	3	1
Полудодекаэдр	{5,3}/2 {5,3}5		6	15	10	1
Полуикосаэдр	{3,5}/2 {3,5}5		10	15	6	1

Правильные проективные многогранники в четырёхмерном пространстве

В 4-мерном пространстве 5 из 6 выпуклых правильных многогранников образуют проективные 4-мерные многогранники. 3 специальных случая — это полудвадцатичетырёхъячейник, полушестисотъячейник и полустодвадцатиячейник.

4-мерные правильные полумногогранники!Название

Символ
Коксетера

Символ
Макмаллена

Ячеек

Граней

Рёбер

Вершин

χ

полутессеракт	{4,3,3}/2	{4,3,3}4	4	12	16	8	0
полушестнадцатиячейник	{3,3,4}/2	{3,3,4}4	8	16	12	4	0
полудвадцатичетырёхъячейник	{3,4,3}/2	{3,4,3}6	12	48	48	12	0
полустодвадцатиячейник	{5,3,3}/2	{5,3,3}15	60	360	600	300	0
полушестисотъячейник	{3,3,5}/2	{3,3,5}15	300	600	360	60	0

Правильные проективные многогранники в пятимерном пространстве

Существует только 2 выпуклых правильных проективных полумногогранника в пространствах размерности 5 и выше.

Название	Шлефли	4D-граней	Ячеек (3D)	Граней (2D)	Рёбер	Вершин	χ
полупентеракт	{4,3,3,3}/2	5	20	40	40	16	1
полупентакросс	{3,3,3,4}/2	16	40	40	20	5	1

Бесконечногранники

Бесконечногранник — это многогранник, имеющий бесконечное число фасет. n-бесконечногранник — это n-мерный бесконечногранник: 2-бесконечногранник = бесконечноугольник (апейрогон), 3-бесконечногранник = бесконечногранник в трёхмерном пространстве и т.д.

Существует два главных геометрических класса бесконечногранников:

• Правильные соты в n-мерном пространстве, полностью заполняющие n-мерное пространство.
• Правильные косые бесконечногранники, содержащие n-мерные многообразия в более высоких пространствах.

Одномерное пространство (бесконечноугольники)

Прямой апейрогон — это правильное замощение прямой с разделением её на бесконечно много равных отрезков. Он имеет бесконечно много вершин и рёбер. Его символ Шлефли равен {∞}, а диаграмма Коксетера — .

......

Апейрогоны на гиперболической плоскости, среди которых наиболее заметен правильный апейрогон {∞}, могут иметь кривизну, наподобие конечных многоугольников на евклидовой плоскости, и иметь вершины, лежащие на орициклах или гиперциклах.

Правильные апейрогоны со сходимостью на бесконечности имеют символ {∞} и существуют на орициклах, хотя в общем случае они могут существовать на гиперциклах.

{∞}	{πi/λ}
Бесконечноугольник на орицикле	Бесконечноугольник на гиперцикле

Выше показаны два гиперболических апейрогона на диске Пуанкаре. На правом рисунке показаны перпендикулярные прямые, разделяющие фундаментальные области, отстоящие на расстояние λ друг от друга.

Пространственные бесконечноугольники

Косые апейрогоны в двумерном пространстве (плоскости) образуют зигзаг. Если зигзаг симметричен и однороден, апейрогон правильный.

Косые апейрогоны можно построить в пространстве любой размерности. В трёхмерном пространстве косые апейрогоны образуют спираль и могут быть левыми или правыми.

Двумерное пространство	Трёхмерное пространство
Апейрогон в виде зигзага	Спиральный апейрогон

Двумерное пространство (бесконечногранники)

Евклидовы мозаики

Существует три правильных замощения плоскости. Все три имеют эйлерову характеристику (χ) 0.

Название	Квадратная мозаика (кадриль)	Треугольная мозаика (дельтаплитка)	Шестиугольный паркет (гексаплитка)
Симметрия	p4m, [4,4], (*442)	p6m, [6,3], (*632)
Шлефли {p,q}	{4,4}	{3,6}	{6,3}
Диаграмма Коксетера
Рисунок

Существует две несобственные правильные мозаики — {∞,2}, бесконечноугольный диэдр, полученный из двух апейрогонов, каждый из которых заполняет полуплоскость, и двойственная ей {2,∞} мозаика, бесконечноугольный осоэдр, который можно представить как бесконечное число параллельных прямых.

{∞,2},

{2,∞},

Евклидовы звёздчатые мозаики

Не существует правильных замощений плоскости звёздчатыми многоугольниками. Существует бесконечно много пар чисел, для которых выполняется условие плоской мозаики (1/p + 1/q = 1/2), например, {8/3,8}, {10/3,5}, {5/2,10}, {12/5,12}, и т.д., но ни одна из этих звёзд не подходит для замощения.

Гиперболические мозаики

Замощения гиперболического двухмерного пространства — это гиперболические мозаики. Существует бесконечно много правильных мозаик в H². Как констатировано выше, любая положительная пара {p,q}, такая что 1/p + 1/q < 1/2 даёт гиперболическую мозаику. Фактически для общего треугольника Шварца (p, q, r) то же самое верно для 1/p + 1/q + 1/r < 1.

Существует много различных путей представления гиперболической плоскости, включая дисковую модель Пуанкаре, в которой плоскость отображается в диск, как показано ниже. Следует рассматривать все многоугольные грани замощения как равносторонние, и многоугольники становятся меньше при приближению к краю диска вследствие применения проекции, что похоже на эффект фотокамеры c объективом «Рыбий глаз».

Существует бесконечно много плоских правильных 3-бесконечногранников как правильных мозаик гиперболической плоскости, имеющих вид {p,q}, где p+q<pq/2.

• {3,7}, {3,8}, {3,9} ... {3,∞}
• {4,5}, {4,6}, {4,7} ... {4,∞}
• {5,4}, {5,5}, {5,6} ... {5,∞}
• {6,4}, {6,5}, {6,6} ... {6,∞}
• {7,3}, {7,4}, {7,5} ... {7,∞}
• {8,3}, {8,4}, {8,5} ... {8,∞}
• {9,3}, {9,4}, {9,5} ... {9,∞}
• ...
• {∞,3}, {∞,4}, {∞,5} ... {∞,∞}

Примеры:

Сферические (Платоновы)/Евклидовы/гиперболические (диск Пуанкаре: компактные/паракомпактные/некомпактные) замощения с их символами Шлефли
p \ q	3	4	5	6	7	8	...	∞	...	iπ/λ
3	(тетраэдр) {3,3}	(октаэдр) {3,4}	(икосаэдр) {3,5}	(дельта-плитка) {3,6}	{3,7}	{3,8}		{3,∞}		{3,iπ/λ}
4	(куб) {4,3}	(кадриль) {4,4}	{4,5}	{4,6}	{4,7}	{4,8}		{4,∞}		{4,iπ/λ}
5	(додекаэдр) {5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}		{5,∞}		{5,iπ/λ}
6	(гексаплитка) {6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}		{6,∞}		{6,iπ/λ}
7	{7,3}	{7,4}	{7,5}	{7,6}	{7,7}	{7,8}		{7,∞}		{7,iπ/λ}
8	{8,3}	{8,4}	{8,5}	{8,6}	{8,7}	{8,8}		{8,∞}		{8,iπ/λ}
...
∞	{∞,3}	{∞,4}	{∞,5}	{∞,6}	{∞,7}	{∞,8}	{∞,∞}	{∞,iπ/λ}
...
iπ/λ	{iπ/λ,3}	{iπ/λ,4}	{iπ/λ,5}	{iπ/λ,6}	{iπ/λ,7}	{iπ/λ,8}	{iπ/λ,∞}	{iπ/λ,iπ/λ}

Гиперболические звёздчатые мозаики

Существует два бесконечных вида гиперболических мозаик, грани или вершинные фигуры которых являются звёздчатыми многоугольниками — {m/2, m} и их двойственные {m, m/2} с m = 7, 9, 11, .... Мозаики {m/2, m} являются звёздчатыми формами мозаик {m, 3}, в то время как двойственные мозаики {m, m/2} являются огранкой мозаик {3, m} и увеличениями мозаик {m, 3}.

Схемы {m/2, m} и {m, m/2} продолжаются для нечётных m < 7 как многогранники: если m = 5, мы получим малый звёздчатый додекаэдр и большой додекаэдр, а при m = 3 мы получим тетраэдр. Другие два тела Кеплера — Пуансо (большой звёздчатый додекаэдр и большой икосаэдр) не имеют аналогов в правильных гиперболических мозаиках. Если m чётно, в зависимости от того, как мы выберем определение {m/2}, мы можем получить либо вырожденное покрытие другой мозаики или соединение мозаик.

Название	Шлефли	Диаграмма Коксетера	Рисунок	Тип грани {p}	Вершинная фигура {q}	Плот- ность	Симметрия	Двойственная
Семиугольная мозаика порядка 7	{7/2,7}			{7/2}	{7}	3	*732 [7,3]	Семиугольная гептаграммная мозаика
Семиугольная гептаграммная мозаика	{7,7/2}			{7}	{7/2}	3	*732 [7,3]	Гептаграммная мозаика порядка7
Эннеаграммная мозаика порядка 9	{9/2,9}			{9/2}	{9}	3	*932 [9,3]	Эннеаграммная девятиугольная мозаика
Эннеаграммная девятиугольная мозаика	{9,9/2}			{9}	{9/2}	3	*932 [9,3]	Эннеаграммная девятиугольная мозаика порядка 9
Гендекаграммная мозаика порядка 11	{11/2,11}			{11/2}	{11}	3	*11.3.2 [11,3]	Гендекаграммная мозаика одиннадцатиугольная мозаика
Гендекаграммная мозаика одиннадцатиугольная мозаика	{11,11/2}			{11}	{11/2}	3	*11.3.2 [11,3]	Гендекаграммная мозаика порядка 11
p- граммная мозаика порядка p	{p/2,p}			{p/2}	{p}	3	*p32 [p,3]	p- граммная p- угольная мозаика
p-граммная мозаика p-угольная мозаика	{p,p/2}			{p}	{p/2}	3	*p32 [p,3]	p-граммная мозаика порядка p

Косые бесконечногранники в евклидовом 3-мерном пространстве

Существует три правильных косых бесконечногранников в евклидовом трёхмерном пространстве с правильным пространственным многоугольником в качестве вершинных фигур . Они имеют то же самое расположение вершин и расположение рёбер, что и у 3 выпуклых однородных сот.

• 6 квадратов вокруг каждой вершины: {4,6|4}
• 4 шестиугольника вокруг каждой вершины: {6,4|4}
• 6 шестиугольников вокруг каждой вершины: {6,6|3}

12 "чистых" бесконечногранников в евклидовом 3-мерном пространстве на основе кубических сот, {4,3,4} . Оператор Петри π заменяет грани многоугольниками Петри. δ является двойственным оператором, обменивающим местами вершины и грани. φ_k является k-м оператором огранки. η является оператором взятия половины, а σ — взятием косой половины.

Правильный косой многоугольник
{4,6|4}	{6,4|4}	{6,6|3}

Существует тридцать правильных бесконечноугольников в евклидовом трёхмерном пространстве . Они включают как перечисленные выше, так и 8 других "чистых" бесконечноугольников. Все они связаны с кубическими сотами {4,3,4}. Остальные имеют пространственные многоугольные грани: {6,6}₄, {4,6}₄, {6,4}₆, {∞,3}^a, {∞,3}^b, {∞,4}^.*3, {∞,4}_6,4, {∞,6}_4,4 и {∞,6}_6,3.

Косые бесконечногранники в гиперболическом трёхмерном пространстве

Существует 31 правильный косой бесконечногранник в гиперболическом трёхмерном пространстве :

• 14 компактных: {8,10|3}, {10,8|3}, {10,4|3}, {4,10|3}, {6,4|5}, {4,6|5}, {10,6|3}, {6,10|3}, {8,8|3}, {6,6|4}, {10,10|3},{6,6|5}, {8,6|3} и {6,8|3}.
• 17 паракомпактных: {12,10|3}, {10,12|3}, {12,4|3}, {4,12|3}, {6,4|6}, {4,6|6}, {8,4|4}, {4,8|4}, {12,6|3}, {6,12|3}, {12,12|3}, {6,6|6}, {8,6|4}, {6,8|4}, {12,8|3}, {8,12|3} и {8,8|4}.

Трёхмерное пространство (4-apeirotopes)

Замощения евклидова трёхмерного пространства

Рёберный каркас кубических сот {4,3,4}

Существует только одно невырожденное правильное замощение 3-мерного пространства (соты), {4, 3, 4} :

Название	Шлефли {p,q,r}	Коксетер	Тип ячейки {p,q}	Тип грани {p}	Рёберная фигура {r}	Вершинная фигура {q,r}	χ	Двойственный
Кубические соты	{4,3,4}		{4,3}	{4}	{4}	{3,4}	0	Самодвойственны

Несобственные замощения евклидова трёхмерного пространства

Правильные соты {2,4,4}, в виде проекции на сферу.

Существует шесть несобственных правильных замощений, попарно основанных на трёх правильных евклидовых замощениях. Их ячейки и вершинные фигуры являются правильными осоэдрами {2,n}, диэдрами {n,2} и евклидовыми мозаиками. Эти несобственные правильные мозаики конструкционно связаны с призматическими однородными сотами операцией усечения. Они являются высокоразмерными аналогами бесконечноугольной мозаики порядка 2 и бесконечноугольного осоэдра.

Шлефли {p,q,r}	Диаграмма Коксетера	Тип ячейки {p,q}	Тип грани {p}	Рёберная фигура {r}	Вершинная фигура {q,r}
{2,4,4}		{2,4}	{2}	{4}	{4,4}
{2,3,6}		{2,3}	{2}	{6}	{3,6}
{2,6,3}		{2,6}	{2}	{3}	{6,3}
{4,4,2}		{4,4}	{4}	{2}	{4,2}
{3,6,2}		{3,6}	{3}	{2}	{6,2}
{6,3,2}		{6,3}	{6}	{2}	{3,2}

Замощения гиперболического трёхмерного пространства

4 компактных правильных сот {5,3,4} {5,3,5} {4,3,5} {3,5,3}

4 из 11 паракомпактных правильных сот {3,4,4} {3,6,3} {4,4,3} {4,4,4}

Существует десять плоских правильных сот гиперболического 3-мерного пространства (перечислены выше как замощения):

• 4 компактных: {3,5,3}, {4,3,5}, {5,3,4} и {5,3,5}
• 6 паракомпактных: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} и {6,3,6}.

Замощения гиперболического 3-мерного пространства можно назвать гиперболическими сотами. Существует 15 гиперболических сот в H³, 4 компактных и 11 паракомпактных.

Название	Символ Шлефли {p,q,r}	Коксетер	Тип ячейки {p,q}	Тип грани {p}	Рёберная фигура {r}	Вершинная фигура {q,r}	χ	Двойственный
Икосаэдральные соты	{3,5,3}		{3,5}	{3}	{3}	{5,3}	0	Самодвойственны
Кубические соты порядка 5	{4,3,5}		{4,3}	{4}	{5}	{3,5}	0	{5,3,4}
Додекаэдральные соты порядка 4	{5,3,4}		{5,3}	{5}	{4}	{3,4}	0	{4,3,5}
Додекаэдральные соты порядка 5	{5,3,5}		{5,3}	{5}	{5}	{3,5}	0	Самодвойственны

Существует также 11 паракомпактных H³ сот (с бесконечными (евклидовыми) ячейками и/или вершинными фигурами): {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} и {6,3,6}.

Название	Символ Шлефли {p,q,r}	Коксетер	Тип ячейки {p,q}	Тпи грани {p}	Рёберная фигура {r}	Вершинная фигура {q,r}	χ	Двойственный
Тетраэдральные соты порядка 6	{3,3,6}		{3,3}	{3}	{6}	{3,6}	0	{6,3,3}
Шестиугольные мозаичные соты	{6,3,3}		{6,3}	{6}	{3}	{3,3}	0	{3,3,6}
Октаэдральные соты порядка 4	{3,4,4}		{3,4}	{3}	{4}	{4,4}	0	{4,4,3}
Квадратные мозаичные соты	{4,4,3}		{4,4}	{4}	{3}	{4,3}	0	{3,3,4}
Треугольные мозаичные соты	{3,6,3}		{3,6}	{3}	{3}	{6,3}	0	Самодвойственны
Кубические соты порядка 6	{4,3,6}		{4,3}	{4}	{4}	{3,4}	0	{6,3,4}
Шестиугольные мозаичные соты порядка 4	{6,3,4}		{6,3}	{6}	{4}	{3,4}	0	{4,3,6}
Квадратные мозаичные соты порядка 4	{4,4,4}		{4,4}	{4}	{4}	{4,4}	0	{4,4,4}
Додекаэдральные соты порядка 6	{5,3,6}		{5,3}	{5}	{5}	{3,5}	0	{6,3,5}
Шестиугольные мозаичные соты порядка 5	{6,3,5}		{6,3}	{6}	{5}	{3,5}	0	{5,3,6}
Шестиугольные мозаичные соты порядка 6	{6,3,6}		{6,3}	{6}	{6}	{3,6}	0	Самодвойственны

Некомпактные решения существуют как лоренцевы группы Коксетера и могут быть визуализированы с помощью открытой области в гиперболическом пространстве (фундаментальный тетраэдрон, имеющий некоторые части недостижимыми ввиду бесконечности), и некоторые нарисованы ниже, показывая их пересечение с плоскостью. Все соты, не показанные в таблицах и не имеющие двойки в их символе Шлефли, являются некомпактными.

Сферические/Евклидовы/гиперболические(компактные/паракомпактные/некомпактные) соты {p,3,r}

p \ r	3	4	5	6	7	8	... ∞
3	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	{3,3,∞}
4	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	{4,3,∞}
5	{5,3,3}	{5,3,4}	{5,3,5}	{5,3,6}	{5,3,7}	{5,3,8}	{5,3,∞}
6	{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{6,3,7}	{6,3,8}	{6,3,∞}
7	{7,3,3}	{7,3,4}	{7,3,5}	{7,3,6}	{7,3,7}	{7,3,8}	{7,3,∞}
8	{8,3,3}	{8,3,4}	{8,3,5}	{8,3,6}	{8,3,7}	{8,3,8}	{8,3,∞}
... ∞	{∞,3,3}	{∞,3,4}	{∞,3,5}	{∞,3,6}	{∞,3,7}	{∞,3,8}	{∞,3,∞}

q = 4	q = 5	q = 6
p \ r 3 4 5 3 {3,4,3} {3,4,4} {3,4,5} 4 {4,4,3} {4,4,4} {4,4,5} 5 {5,4,3} {5,4,4} {5,4,5}	p \ r 3 4 3 {3,5,3} {3,5,4} 4 {4,5,3} {4,5,4} 5 {5,5,3} {5,5,4}	p \ r 3 4 3 {3,6,3} {3,6,4} 4 {4,6,3} {4,6,4} 5 {5,6,3} {5,6,4}

Не существует гиперболических звёздчатых сот в H³ — все формы с правильным звёздчатым многогранником в качестве ячейки, вершинной фигуры, или того и другого оказываются сферическими.

Четырёхмерное пространство (5-бесконечногранники)

Замощения евклидов 4-мерного пространства

Существует три вида бесконечных правильных (сот), которые могут заполнить евклидово четырёхмерное пространство:

Название	Символ Шлефли {p,q,r,s}	Тип фасеты {p,q,r}	Тип ячейки {p,q}	Тип грани {p}	Фигура грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}	Двойственный
Тессерактные соты	{4,3,3,4}	{4,3,3}	{4,3}	{4}	{4}	{3,4}	{3,3,4}	Самодвойственены
Шестнадцатиячейные соты	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,4,3,3}
Двадцати- четырёхъячейные соты	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{4,3,3}	{3,3,4,3}

Спроецированный фрагмент сот {4,3,3,4} (Тессерактовые соты)

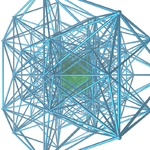Спроецированный фрагмент сот {3,3,4,3} (Шестнадцатиячейные соты)

Спроецированный фрагмент сот {3,4,3,3} (24-ячейные соты)

Существует также два несобственных случая, {4,3,4,2} и {2,4,3,4}. Существует три плоских правильных вида сот евклидова 4-мерного пространства:

• {4,3,3,4}, {3,3,4,3} и {3,4,3,3}.

Существует семь плоских правильных выпуклых сот гиперболического 4-мерного пространства:

• 5 компактных: {3,3,3,5}, {5,3,3,3}, {4,3,3,5}, {5,3,3,4}, {5,3,3,5}
• 2 паракомпактных: {3,4,3,4} и {4,3,4,3}.

Существует четыре плоских правильных звёздчатых видов сот в гиперболическом 4-мерном пространстве:

• {5/2,5,3,3}, {3,3,5,5/2}, {3,5,5/2,5} и {5,5/2,5,3}.

Замощения гиперболического 4-мерного пространства

Существует семь выпуклых правильных сот и четыре звёздчатые формы сот в пространстве H⁴ . Пять выпуклых видов компактны, а два паракомпактны.

Пять компактных правильных сот в H⁴:

Название	Символ Шлефли {p,q,r,s}	Тип фасеты {p,q,r}	Тип ячейки {p,q}	Тип грани {p}	Фигура грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}	Двойственный
Пятиячейные соты порядка 5	{3,3,3,5}	{3,3,3}	{3,3}	{3}	{5}	{3,5}	{3,3,5}	{5,3,3,3}
120-ячейные соты	{5,3,3,3}	{5,3,3}	{5,3}	{5}	{3}	{3,3}	{3,3,3}	{3,3,3,5}
Тессерактные соты порядка 5	{4,3,3,5}	{4,3,3}	{4,3}	{4}	{5}	{3,5}	{3,3,5}	{5,3,3,4}
120-ячейные соты порядка 4	{5,3,3,4}	{5,3,3}	{5,3}	{5}	{4}	{3,4}	{3,3,4}	{4,3,3,5}
120-ячейные соты порядка 5	{5,3,3,5}	{5,3,3}	{5,3}	{5}	{5}	{3,5}	{3,3,5}	Самодвойственен

Два правильных паракомпактных правильных вида сот в H⁴: {3,4,3,4}, {4,3,4,3}.

Название	Символ Шлефли {p,q,r,s}	Тип фасеты {p,q,r}	Тип ячейки {p,q}	Тип грани {p}	Фигура грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}	Двойственный
24-ячейные соты порядка 4	{3,4,3,4}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{4,3,4}	{4,3,4,3}
Кубические сотовые соты	{4,3,4,3}	{4,3,4}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,4,3,4}

Некомпактные решения существуют как лоренцевы группы Коксетера и могут быть визуализированы с помощью открытой области в гиперболическом пространстве (фундаментальный пятиячейник, имеющий некоторые части недостижимыми ввиду бесконечности). Все соты, не показанные в таблицах и не имеющие двойки в их символе Шлефли, являются некомпактными.

Сферические/Евклидовы/гиперболические(компактные/паракомпактные/некомпактные) соты {p,q,r,s}

q=3, s=3 p \ r 3 4 5 3 {3,3,3,3} {3,3,4,3} {3,3,5,3} 4 {4,3,3,3} {4,3,4,3} {4,3,5,3} 5 {5,3,3,3} {5,3,4,3} {5,3,5,3}	q=3, s=4 p \ r 3 4 3 {3,3,3,4} {3,3,4,4} 4 {4,3,3,4} {4,3,4,4} 5 {5,3,3,4} {5,3,4,4}	q=3, s=5 p \ r 3 4 3 {3,3,3,5} {3,3,4,5} 4 {4,3,3,5} {4,3,4,5} 5 {5,3,3,5} {5,3,4,5}
q=4, s=3 p \ r 3 4 3 {3,4,3,3} {3,4,4,3} 4 {4,4,3,3} {4,3,4,3}	q=4, s=4 p \ r 3 4 3 {3,4,3,4} {3,4,4,4} 4 {4,4,3,4} {4,4,4,4}	q=4, s=5 p \ r 3 4 3 {3,4,3,5} {3,4,4,5} 4 {4,4,3,5} {4,4,4,5}

Звёздчатые замощения гиперболического 4-мерного пространства

Существует четыре вида правильных звёздчатых сот в пространстве H⁴:

Название	Символ Шлефли {p,q,r,s}	Тип фасеты {p,q,r}	Тип ячейки type {p,q}	Тип грани {p}	Фигура грани {s}	Рёберная фигура {r,s}	Вершинная фигура {q,r,s}	Двойственный	Плот- ность
Соты из малого звёздчатого 120-ячейника	{5/2,5,3,3}	{5/2,5,3}	{5/2,5}	{5}	{5}	{3,3}	{5,3,3}	{3,3,5,5/2}	5
600-ячейник пентаграммного порядка	{3,3,5,5/2}	{3,3,5}	{3,3}	{3}	{5/2}	{5,5/2}	{3,5,5/2}	{5/2,5,3,3}	5
Икосаэдральные 120-ячейные соты порядка 5	{3,5,5/2,5}	{3,5,5/2}	{3,5}	{3}	{5}	{5/2,5}	{5,5/2,5}	{5,5/2,5,3}	10
Соты большого 120-ячейника	{5,5/2,5,3}	{5,5/2,5}	{5,5/2}	{5}	{3}	{5,3}	{5/2,5,3}	{3,5,5/2,5}	10

Пятимерное пространство (бесконечноугольные 6-многогранники)

Существуют только одни плоские правильные соты в евклидовом 5-мерном пространстве: ( перечислены выше как замощения)

• {4,3,3,3,4}

Существует пять плоских правильных сот гиперболического 5-мерного пространства, все паракомпактные: (перечислены выше как замощения)

• {3,3,3,4,3}, {3,4,3,3,3}, {3,3,4,3,3}, {3,4,3,3,4} и {4,3,3,4,3}

Замощение s евклидова 5-мерного пространства

Гиперкубические соты является единственным семейством правильных сот, которые могут замостить пространство любой размерности (пять и выше), образованные фасетами-гиперкубами, по четыре вокруг каждой (n-2)-мерной грани.

Название	Шлефли {p1, p2, ..., pn−1}	Тип фасеты	Вершинная фигура	Двойственный
Квадратный паркет	{4,4}	{4}	{4}	Самодвой- ственен
Кубические соты	{4,3,4}	{4,3}	{3,4}	Самодвой- ственны
Тессерактные соты	{4,32,4}	{4,32}	{32,4}	Самодвой- ственны
5-кубические соты	{4,33,4}	{4,33}	{33,4}	Самодвой- ственны
6-кубические соты	{4,34,4}	{4,34}	{34,4}	Самодвой- ственны
7-кубические соты	{4,35,4}	{4,35}	{35,4}	Самодвой- ственны
8-кубические соты	{4,36,4}	{4,36}	{36,4}	Самодвой- ственны
n-мерные гиперкубические соты	{4,3n−2,4}	{4,3n−2}	{3n−2,4}	Самодвой- ственны

В E⁵ существуют также несобственные случаи {4,3,3,4,2}, {2,4,3,3,4}, {3,3,4,3,2}, {2,3,3,4,3}, {3,4,3,3,2} и {2,3,4,3,3}. В Eⁿ, {4,3ⁿ⁻³,4,2} и {2,4,3ⁿ⁻³,4} являются всегда несобственными евклидовыми замощениями.

Замощения гиперболического 5-мерного пространства

Существует 5 правильных видов сот в H⁵, все паракомпактные. Они включают бесконечные (евклидовы) фасеты или вершинные фигуры: {3,4,3,3,3}, {3,3,4,3,3}, {3,3,3,4,3}, {3,4,3,3,4} и {4,3,3,4,3}.

Существует два некомпактных правильных замощения гиперболического пространстваразмерности 5 и выше и нет паракомпактных правильных замощений в гиперболическом пространстве размерности 6 и выше.

Название	Символ Шлефли {p,q,r,s,t}	Тип фасеты {p,q,r,s}	4-face type {p,q,r}	Cell type {p,q}	Face type {p}	Cell figure {t}	Face figure {s,t}	Edge figure {r,s,t}	Вершинная фигура {q,r,s,t}	Двойственный
5-ортоплексные соты	{3,3,3,4,3}	{3,3,3,4}	{3,3,3}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,3}
Двадцати- четырёхъячейные сотовые соты	{3,4,3,3,3}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{3,3,3}	{4,3,3,3}	{3,3,3,4,3}
Шестнадцатиячейные сотовые соты	{3,3,4,3,3}	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{3,3}	{4,3,3}	{3,4,3,3}	Самодвой- ственны
24-ячейные соты порядка 4	{3,4,3,3,4}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{3,3,4}	{4,3,3,4}	{4,3,3,4,3}
Тессерактные сотовые соты	{4,3,3,4,3}	{4,3,3,4}	{4,3,3}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,4}

Поскольку не существует правильных звёздчатых n-многогранников для n ≥ 5, которые могли бы быть потенциальными ячейками или вершинными фигурами, не существует больше гиперболических звёздчатых сот в Hⁿ для n ≥ 5.

Размерность 6 и выше (7-мерные бесконечногранники+)

Замощения гиперболического 6-мерного и выше пространства

Не существует правильных компактных или паракомпактных замощений гиперболического пространства размерности 6 или выше. Все целые неперчисленные значения дают некомпактное замощение гиперболического n-мерного пространства.

Соединения многогранников

Основная статья: Соединение многогранников

Двухмерные соединения

Для любого натурального числа n существует n-вершинный звёздчатый правильный многоугольник с символом Шлефли {n/m} для любого m < n/2 (строго говоря, {n/m}={n/(n−m)}), где m и n взаимно просты. Если m и n не взаимно просты, полученный многоугольник будет иметь n/m сторон. Новая фигура получается вращением этих n/m-угольников на одну вершину (влево), пока число вращений не достигнет числа n/m минус единица, и комбинацией этих повёрнутых фигур. В экстремальном случае, когда n/m равно 2, получим фигуру из n/2 отрезков. Такая фигура называется вырожденным звёздчатым многоугольником.

В других случаях, когда n и m имеют общий делитель, получим звёздчатый многоугольник с меньшим n и с ним можно скомбинировать версии, полученные вращением. Эти фигуры называются звёздчатыми фигурами, несобственными звёздчатыми многоугольниками или соединениями многоугольников. Для них часто используется то же обозначение {n/m}, хотя некоторые авторы, такие как Грюнбаум (1994), предпочитают (с некоторыми уточнениями) форму k{n} как более правильную, где, обычно, k = m.

Следующее усложнение возникает, когда мы соединяем два или более звёздчатых многоугольника, как, например, две пентаграммы, отличающиеся поворотом на 36° и вписанные в десятиугольник. Правильнее в этом случае писать в виде k{n/m}, в нашем случае 2{5/2}, а не использовать обычно используемое {10/4}.

Расширенная нотация Коксетера для соединения многоугольников имеет вид c{m,n,...}[d{p,q,...}]e{s,t,...}, в которой отражается, что d различных {p,q,...} вместе покрывают вершины {m,n,...} c раз и грани {s,t,...} e раз. Если не существует правильного {m,n,...}, первая часть записи удаляется, оставляя [d{p,q,...}]e{s,t,...}. Противоположный случай — если не существует правильного {s,t,...}. Двойственным к of c{m,n,...}[d{p,q,...}]e{s,t,...} является e{t,s,...}[d{q,p,...}]c{n,m,...}. Если c или e равно 1, их можно опускать. Для соединения многоугольников эта нотация сводится к {nk}[k{n/m}]{nk}. Например, гексаграмму можно записать как {6}[2{3}]{6}.

Примеры для n=2..10, nk≤30

2{2}

3{2}

4{2}

5{2}

6{2}

7{2}

8{2}

9{2}

10{2}

11{2}

12{2}

13{2}

14{2}

15{2}

2{3}

3{3}

4{3}

5{3}

6{3}

7{3}

8{3}

9{3}

10{3}

2{4}

3{4}

4{4}

5{4}

6{4}

7{4}

2{5}

3{5}

4{5}

5{5}

6{5}

2{5/2}

3{5/2}

4{5/2}

5{5/2}

6{5/2}

2{6}

3{6}

4{6}

5{6}

2{7}

3{7}

4{7}

2{7/2}

3{7/2}

4{7/2}

2{7/3}

3{7/3}

4{7/3}

2{8}

3{8}

2{8/3}

3{8/3}

2{9}

3{9}

2{9/2}

3{9/2}

2{9/4}

3{9/4}

2{10}

3{10}

2{10/3}

3{10/3}

2{11}

2{11/2}

2{11/3}

2{11/4}

2{11/5}

2{12}

2{12/5}

2{13}

2{13/2}

2{13/3}

2{13/4}

2{13/5}

2{13/6}

2{14}

2{14/3}

2{14/5}

2{15}

2{15/2}

2{15/4}

2{15/7}

Правильные пространственные многоугольники также создают соединения, которые можно наблюдать в рёбрах призматического соединения антипризм, например:

Правильные соединения пространственных многоугольников

Соединение пространственных квадратов		Соединение пространственных шестиугольников	Соединение пространственных десятиугольников
Два {2}#{ }	Три {2}#{ }	Два {3}#{ }	Два {5/3}#{ }

Трёхмерные соединения

Правильные соединения многогранников можно определить как соединения, которые, подобно правильным многогранников, вершинно транзитивны, рёберно транзитивны и транзитивны по граням. По этому определению имеется 5 правильных соединений.

Симметрия	[4,3], Oh	[5,3]+, I	[5,3], Ih
Двойственность	Самодвойственный			Двойственные пары
Рисунок
Сферические
Многогранники	Звёздчатый октаэдр	5 {3,3}	10 {3,3}	5 {4,3}	5 {3,4}
Коксетер	{4,3}[2{3,3}]{3,4}	{5,3}[5{3,3}]{3,5}	2{5,3}[10{3,3}]2{3,5}	2{5,3}[5{4,3}]	[5{3,4}]2{3,5}

Соединения на евклидовой и гиперболической плоскостях

Существует восемнадцать двупараметрических семейств правильных соединений мозаик евклидовой плоскости. На гиперболической плоскости известны пять однопараметрических семейств и семнадцать изолированных случаев, но полнота этого списка ещё не доказана.

Семейства соединений евклидовой и гиперболической плоскостей 2 {p,p} (4 ≤ p ≤ ∞, p целое) аналогичны сферическим звёздчатым октаэдрам, 2 {3,3}.

Несколько примеров евклидовых и гиперболических правильных соединений

Самодвойственные	Самодвойственные		Самодвойственные
2 {4,4}	2 {6,3}	2 {3,6}	2 {∞,∞}
{{4,4}} или a{4,4} или {4,4}[2{4,4}]{4,4} + или	[2{6,3}]{3,6}	a{6,3} или {6,3}[2{3,6}] + или	{{∞,∞}} или a{∞,∞} или {4,∞}[2{∞,∞}]{∞,4} + или
	3 {6,3}	3 {3,6}	3 {∞,∞}
	2{3,6}[3{6,3}]{6,3}	{3,6}[3{3,6}]2{6,3} + +	+ +

Соединения в четырёхмерном пространстве

Ортогональные проекции

75 {4,3,3}	75 {3,3,4}

В 4-мерном пространстве существует тридцать два правильных соединения правильных многогранников, которые Коксетер перечислил в своей книге Regular Polytopes:

Самодвойственные правильные соединения

Соединение	Симметрия	Расположение вершин	Расположение ячеек
120 {3,3,3}	[5,3,3], порядок 14400	{5,3,3}	{3,3,5}
5 {3,4,3}	[5,3,3], порядок 14400	{3,3,5}	{5,3,3}

Правильные соединения как двойственные пары

Соединение 1	Соединение 2	Симметрия	Расположение вершин (1)	Расположение ячеек (1)	Расположение вершин (2)	Расположение ячеек (2)
3 {3,3,4}	3 {4,3,3}	[3,4,3], порядок 1152	{3,4,3}	2{3,4,3}	2{3,4,3}	{3,4,3}
15 {3,3,4}	15 {4,3,3}	[5,3,3], порядок 14400	{3,3,5}	2{5,3,3}	2{3,3,5}	{5,3,3}
75 {3,3,4}	75 {4,3,3}	[5,3,3], порядок 14400	5{3,3,5}	10{5,3,3}	10{3,3,5}	5{5,3,3}
75 {3,3,4}	75 {4,3,3}	[5,3,3], порядок 14400	{5,3,3}	2{3,3,5}	2{5,3,3}	{3,3,5}
300 {3,3,4}	300 {4,3,3}	[5,3,3]+, порядок 7200	4{5,3,3}	8{3,3,5}	8{5,3,3}	4{3,3,5}
600 {3,3,4}	600 {4,3,3}	[5,3,3], порядок 14400	8{5,3,3}	16{3,3,5}	16{5,3,3}	8{3,3,5}
25 {3,4,3}	25 {3,4,3}	[5,3,3], порядок 14400	{5,3,3}	5{5,3,3}	5{3,3,5}	{3,3,5}

Существует два различных соединения 75 тессерактов: одно использует те же вершины, что и стодвадцатиячейник, а другое использует те же вершины, что и шестисотъячейник. Отсюда следует, что соответствующие двойственные соединения 75 шестнадцатиячейников также различны.

Самодвойственные звёздчатые соединения

Соединение	Симметрия	Расположение вершин	Расположение ячеек
5 {5,5/2,5}	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}
10 {5,5/2,5}	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}
5 {5/2,5,5/2}	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}
10 {5/2,5,5/2}	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}

Правильные звёздчатые соединения как двойственные пары

Соединение1	Соединение2	Симметрия	Расположение вершин (1)	Расположение ячеек (1)	Расположение вершин (2)	Расположение ячеек (2)
5 {3,5,5/2}	5 {5/2,5,3}	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {3,5,5/2}	10 {5/2,5,3}	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}
5 {5,5/2,3}	5 {3,5/2,5}	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {5,5/2,3}	10 {3,5/2,5}	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}
5 {5/2,3,5}	5 {5,3,5/2}	[5,3,3]+, порядок 7200	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {5/2,3,5}	10 {5,3,5/2}	[5,3,3], порядок 14400	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}

Существует также четырнадцать частично правильных соединений, которые либо вершинно-транзитивны, либо ячеечно-транзитивны, но не одновременно. Семь вершинно-транзитивных частично правильных соединений являются двойственными семи ячейно-транзитивным частично правильным соединениям.

Частично правильные соединения как двойственные пары

Соединение 1 вершинно транзитивны	Соединение 2 ячейно транзитивны	Симметрия
2 шестнадцатиячейника	2 тессеракта	[4,3,3], порядок 384
100 двадцатичетырёхъячейников	100 двадцатичетырёхъячейников	[5,3,3]+, порядок 7200
200 двадцатичетырёхъячейников	200 двадцатичетырёхъячейников	[5,3,3], порядок 14400
5 шестисотъячейников	5 стодвадцатиячейников	[5,3,3]+, порядок 7200
10 шестисотъячейников	10 стодвадцатиячейников	[5,3,3], порядок 14400

Частично правильные звёздчатые соединения как двойственные пары

Соединение1 вершинно транзитивны	Соединение2 ячейно транзитивны	Симметрия
5 {3,3,5/2}	5 {5/2,3,3}	[5,3,3]+, порядок 7200
10 {3,3,5/2}	10 {5/2,3,3}	[5,3,3], порядок 14400

Соединения в евклидовом 3-мерном пространстве

Единственными правильными евклидовыми соединениями сот является бесконечное семейство соединений кубических сот, имеющих общие вершины и грани с другими кубическими сотами. Это соединение может иметь любое число кубических сот. Запись Коксетера — {4,3,4}[d{4,3,4}]{4,3,4}.

Соединения в пятимерном и выше пространствах

Нет правильных соединений в пятимерном и шестимерном пространствах. Известны три семимерных соединения (16, 240 и 480 7-симплексов) и шесть восьмимерных (16, 240 и 480 октерактов или 8-ортоплексов). Существует также одно соединение n-мерных симплексов в n-мерном пространстве, при условии, что n на единицу меньше степени двойки, а также два соединения (соединение n-мерных кубов и двойственное ему соединение n-мерных ортоплексов) в n-мерном пространстве, если n является степенью двойки.

Запись Коксетера для этих соединений (где αⁿ = {3ⁿ⁻¹}, βⁿ = {3ⁿ⁻²,4}, γ_n = {4,3ⁿ⁻²}:

• 7-симплексы: cγ₇[16cα₇]cβ₇, where c = 1, 15 или 30
• 8-ортоплексы: cγ₈[16cβ₈]
• 8-кубы: [16cγ₈]cβ₈

Общий случай (когда n = 2^k and d = 2^{2k − k − 1}, k = 2, 3, 4, ...):

• Симплексы: γ_n−1[dα_n−1]β_n−1
• Ортоплексы: γ_n[dβ_n]
• Гиперкубы: [dγ_n]β_n

Соединение евклидовых сот

Известно бесконечное семейство правильных евклидовых соединений сот в размерностях пять и выше — соединение гиперкубических сот, разделяющих вершины и грани с другими гиперболическими сотами. Это соединение может иметь произвольное число гиперболических сот. Запись Коксетера для этих соединений — δ_n[dδ_n]δ_n where δ_n = {∞} при n = 2 и {4,3ⁿ⁻³,4} при n ≥ 3.

Абстрактные многогранники

Понятие абстрактного многогранника возникло при попытке изучать многогранники без привязки их к геометрическому пространству, в котором они находятся. Они включают замощения сферического, евклидова и гиперболического пространств, замощения других многообразий и много других объектов, не имеющих хорошо определённой топологии, но, зато, характеризующихся их "локальной" топологией. Абстрактных многогранников существует бесконечно много в любой размерности. См. атлас для примеров. Некоторые заметные примеры абстрактных правильных многогранников, которые трудно найти где-либо, это одиннадцатиячейник, {3,5,3} и пятидесятисемиячейник, {5,3,5}, имеющие правильные проективные многогранники в качестве ячеек и вершинных фигур.

Элементами абстрактного многогранника являются его тело (максимальный элемент), грани, рёбра, вершины и нулевой многогранник (пустое множество). Эти абстрактные элементы могут быть отображены в обычное пространство или приняты как геометрические фигуры. Некоторые абстрактные многогранники имеют правильно построенную или правдоподобную реализацию, другие таковой не имеют. Флаг — это множество связанных элементов каждой размерности. Для четырёхмерного многогранника — это тело, грань, ребро этой грани, вершина ребра и нулевой многогранник. Говорят, что абстрактный многогранник является правильным, если его комбинаторные симметрии транзитивны на его флагах, то есть любой его флаг может быть переведён симметрией многогранника в любой другой. Абстрактные правильные многогранники являются активной областью исследований.

Пять таких правильных абстрактных многогранников, которые нельзя реализовать правдоподобно, были приведены Коксетером в его книге Regular Polytopes (1977), а затем в статье Уиллса (J. M. Wills) "The combinatorially regular polyhedra of index 2" (1987) . Они топологически эквивалентны тороиду. Их построение путём расположения n граней около каждой вершины можно продолжать бесконечно, давая замощение гиперболической плоскости.

Многогранник	Средний Ромботриаконтаэдр	Додекододекаэдр	Средний триамбикикосаэдр	Битригональный додекаэдр	Выемчатый додекаэдр
Вершинная фигура	{5}, {5/2}	(5.5/2)2	{5}, {5/2}	(5.5/3)3
Грани	30 ромбов	12 пятиугольников 12 пентаграмм	20 шестиугольников	12 пятиугольников 12 пентаграмм	20 гексаграмм
Мозаика	{4, 5}	{5, 4}	{6, 5}	{5, 6}	{6, 6}{6, 6}
χ	−6	−6	−16	−16	−20

Они появляются как двойственные пары:

• Средний ромбический триаконтаэдр и додекододекаэдр двойственны друг другу.
• Средний триамбикикосаэдр и Битригональный додекаэдр двойственны друг другу.
• Выемчатый додекаэдр самодвойственен.

См. также

• Многоугольник
  • Правильный многоугольник
  • Звёздчатый многоугольник
• Многогранник
  • Правильный многогранник (5 правильных платоновых тел и 4 тела Кеплера — Пуансо)
    • Однородный многогранник
• Четырёхмерный многогранник
  • Правильный четырёхмерный многогранник (16 regular 4-polytopes, 4 convex and 10 star (Schläfli–Hess))
  • Однородный четырёхмерный многогранник
• Паркет (геометрия)
  • Замощение евклидовой плоскости правильными многоугольниками
  • Выпуклые однородные соты
• Правильные многомерные многогранники
  • Однородный четырёхмерный многогранник
• Правильная карта

Ссылки

• Платоновы тела
• тела Кеплера — Пуансо
• Regular 4d Polytope Foldouts
• Multidimensional Glossary (См. Hexacosichoron и Hecatonicosachoron)
• Polytope Viewer
• Polytopes and optimal packing of p points in n dimensional spheres
• Атлас малых правильных многогранников
• Regular polyhedra through time I. Hubard, Polytopes, Maps and their Symmetries