Треугольная призма (Mjyrikl,ugx hjn[bg)

Треугольная призма — призма с тремя боковыми гранями. Этот многогранник имеет в качестве граней треугольное основание, его копию, полученную в результате параллельного переноса и 3 грани, соединяющие соответствующие стороны^[англ.]. Прямая треугольная призма имеет прямоугольные боковые стороны, в противном случае призма называется косой.

Однородная треугольная призма — это прямая треугольная призма с равносторонним основанием и квадратными боковыми сторонами.

Призма является пятигранником, у которого две грани параллельны, в то время как нормали трёх других лежат в одной плоскости (которая не обязательно параллельна основаниям). Эти три грани являются параллелограммами. Все сечения, параллельные основаниям, являются одинаковыми треугольниками.

Полуправильный (однородный) многогранник

Прямая треугольная призма является полуправильным многогранником или, более обще, однородным многогранником, если основание является правильным треугольником, а боковые стороны — квадратами.

Этот многогранник можно рассматривать как усечённый треугольный осоэдр, представленный символом Шлефли t{2,3}. Его также можно рассматривать как прямое произведение треугольника на отрезок, что представляется как {3}x{}. Двойственным многогранником треугольной призмы является треугольная бипирамида.

Группой симметрии прямой призмы с треугольным основанием является D_3h порядка 12. Группой вращения служит D₃ с порядком 6. Группа симметрии не содержит центральную симметрию.

Объём

Объём любой призмы равен произведению площади основания на расстояние между основаниями. В нашем случае, когда основание треугольно, нужно просто вычислить площадь треугольника и умножить на длину призмы:

$V={\frac {1}{2}}bhl$ где b — длина стороны основания, h равна высоте треугольника, а l равна расстоянию между треугольниками.

Усечённая треугольная призма

Усечённая прямая треугольная призма имеет одну усечённую треугольную грань^[1].

Гранение

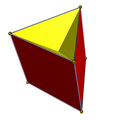
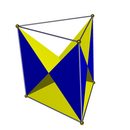
Имеется полная D_2h симметрия гранений^[англ.] (удаление части многогранника, не создавая новые вершины, пересечение рёбер новоё вершиной не считается) треугольной призмы. Получающиеся многогранники имеются многогранники с 6 гранями в виде равнобедренного треугольника, один многогранник сохраняет исходные верхний и нижний треугольники, и один сохраняет исходные квадраты. Две симметрии гранения C_3v имеют один базовый треугольник, 3 грани в виде боковых самопересекающихся квадратов и 3 грани в виде равнобедренных треугольников.

Выпуклые	Гранение
Симметрия D_3h			Симметрия C_3v

2 {3} 3 {4}	3 {4} 6 () v { }	2 {3} 6 () v { }	1 {3} 3 t'{2}^[англ.] 6 () v { }	1 {3} 3 t'{2}^[англ.] 3 () v { }

Связанные многогранники и мозаики

Семейство правильных призм
Конфигурация	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	17.4.4	∞.4.4
Многоугольник
Мозаика

Семейство выпуклых куполов
n	2	3	4	5	6
Название	{2} \|\| t{2}	{3} \|\| t{3}	{4} \|\| t{4}	{5} \|\| t{5}	{6} \|\| t{6}
Купол	Диагональный купол	Трёхскатный купол	Четырёхскатный купол	Пятискатный купол	Шестискатный купол (плоский)
Связанные однородные многогранники	Треугольная призма	Кубооктаэдр	Ромбокубо- октаэдр	Ромбоикосо- додекаэдр	Ромботри- шестиугольная мозаика^[англ.]

Варианты симметрии

Этот многогранник топологически является частью последовательности однородных усечённых многогранников с вершинными конфигурациями (3.2n.2n) и имеющими симметрию [n,3] группы Коксетера.

Варианты симметрии *n32 усечённых мозаик: 3.2n.2n
Симметрия *n32 [n,3]	Сферическая				Евклидова	Компактная гиперболич.		Параком- пактная	Некомпактная гиперболич.
Симметрия *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Усечённые фигуры
Конфигурация	3.4.4	3.6.6	3.8.8	3.10.10	3.12.12^[англ.]	3.14.14^[англ.]	3.16.16^[англ.]	3.∞.∞^[англ.]	3.24i.24i	3.18i.18i	3.12i.12i
Разделённые фигуры
Конфигурация	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12^[англ.]	V3.14.14^[англ.]	V3.16.16	V3.∞.∞

Этот многогранник топологически является частью последовательности рёберно усечённых^[англ.] многогранников с вершинной фигурой (3.4.n.4), которая продолжается как умощения гиперболической плоскости. Эти вершинно-транзитивные^[англ.] фигуры имеют зеркальную симметрию^[англ.] (*n32).

Варианты симметрии *n42 расширенных мозаик: 3.4.n.4
Симметрия *n32 [n,3]	Сферическая				Евклидова	Компактная гиперболическая		Паракомпактная
Симметрия *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Фигура
Конфигурация	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4^[англ.]	3.4.7.4^[англ.]	3.4.8.4^[англ.]	3.4.∞.4^[англ.]

Составные тела

Имеется 4 однородных составных тела из треугольных призм:

Соты

Существует 9 однородных сот, которые включают треугольные призмы:

Связанные многогранники

Треугольная призма является первой в пространственной серии полуправильных многогранников^[англ.]. Каждый последующий однородный многогранник имеет в качестве вершинной фигуры предыдущий многогранник. Торольд Госсет^[англ.] обнаружил эту серию в 1900 году как содержащую все виды граней правильных многомерных многогранников, содержащую все симплексы и ортоплексы (правильные треугольники и квадраты в случае треугольной призмы). В нотации Коксетера^[англ.] треугольной призме соответствует символ −1₂₁.

k₂₁^[англ.] в пространстве размерности n
Пространство	Конечное						Евклидово	Гиперболическое
E_n^[англ.]	3	4	5	6	7	8	9	10
Группа Коксетера	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇^[англ.]	E₈	E₉ = Ẽ₈ = E₈⁺	E₁₀ = T₈ = E₈⁺⁺
Диаграмма Коксетера
Симметрия^[англ.]	[3^−1,2,1]	[3^0,2,1]	[3^1,2,1]	[3^2,2,1]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
Порядок	12	120	192	51 840	2 903 040	696 729 600	∞
Граф							-	-
Обозначение	−1₂₁	0₂₁	1₂₁	2₂₁^[англ.]	3₂₁^[англ.]	4₂₁^[англ.]	5₂₁^[англ.]	6₂₁^[англ.]

Четырёхмерное пространство

Треугольная призма существует как ячейка в большом числе четырёхмерных однородных четырёхмерных многогранников^[англ.], включая:

тетраэдральная призма^[англ.]	октаэдральная призма^[англ.]	кубооктаэдрическая призма^[англ.]	икосаэдральная призма^[англ.]	икосододекаэдральная призма^[англ.]	усечённая додекаэдральная призма^[англ.]

Ромбоикосидодекаэдральная призма^[англ.]	Ромбокубоктаэдральная призма^[англ.]	Усечённая кубическая призма^[англ.]	Плосконосая додекаэдральная призма^[англ.]	n-угольная антипризматическая призма^[англ.]

Рёберноусечённая 5-ячейка^[англ.]	Кантиусечённая 5-ячейка^[англ.]	Рансинированная 5-ячейка^[англ.]	Рансиусечённая 5-ячейка^[англ.]	Cantellated tesseract	Кантиусечённый тессеракт^[англ.]	Рансинированный тессеракт^[англ.]	Рансиусечённый тессеракт^[англ.]

Кантелированная 24-ячейка^[англ.]	Кантиусечённая 24-ячейка^[англ.]	Рансинированная 24-ячейка^[англ.]	Рансиусечённая 24-ячейка^[англ.]	Кантелированная 120-ячейка^[англ.]	Кантиусечённая 120-ячейка^[англ.]	Рансинированная 120-ячейка^[англ.]	Рансиусечённая 120-ячейка^[англ.]