Треугольный паркет (Mjyrikl,udw hgjtym)
| Треугольная мозаика | |
|---|---|

| |
| Тип | Правильная мозаика |
| Вершинная фигура | 3.3.3.3.3.3 (36) |
| Символ Шлефли | {3,6} |
| Символ Витхоффа[англ.] | 6 | 3 2 3 | 3 3 | 3 3 3 |
| Диаграмма Коксетера | |
| Группа симметрии | p6m[англ.], [6,3], (*632) |
| Вращательная симметрия | p6[англ.], [6,3]+, (632) p3, [3[3]]+, (333) |
| Двойственная мозаика |
Шестиугольная мозаика |
| Свойства | Вершинно транзитивна, рёберно транзитивна[англ.], транзитивна по граням[англ.] |
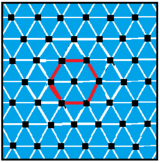
Треуго́льный парке́т (треугольный паркета́ж[1]) или треугольная мозаика — это замощение плоскости равными правильными треугольниками, расположенными сторона к стороне.
Треугольная мозаика является двойственной шестиугольной мозаике — если соединить центры смежных треугольников, то проведённые отрезки дадут шестиугольную мозаику[1][2]. Символ Шлефли треугольного паркета — {3,6}, что означает, что в каждой вершине паркета сходятся 6 треугольников.
Внутренний угол правильного треугольника равен 60 градусов, так что шесть треугольника в одной вершине дают вместе 360 градусов. Это одна из трёх правильных мозаик плоскости. Другие две мозаики — шестиугольный паркет и квадратный паркет.

Английский математик Конвей называл мозаику deltille (дельта-мозаикой), поскольку она имеет форму греческой буквы дельта (Δ). Треугольную мозаику можно также назвать кис-шестиугольной мозаикой, если применить операцию kis[англ.], которая добавляет центральную вершину и треугольники, разбивая грани шестиугольной мозаики.
Однородные раскраски
[править | править код]Существует 9 различных однородных раскрасок треугольной мозаики (по цветам 6 треугольников вокруг вершины — 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314). Три из них можно получить их других путём замены цветов — 111212 и 111112 из 121213, комбинируя 1 и 3, в то время как 111213 получается из 121314[3].
Существует один класс архимедовой раскраски[англ.]*, 111112, (помечен *), в котором раскраска не является 1-однородной и содержит перемежающиеся ряды треугольников, в которых каждый третий выкрашен. Приведённая раскраска является 2-однородной и таких имеется бесконечно много, поскольку такие раскраски определяются произвольными сдвигами строк.
| 111111 | 121212 | 111222 | 112122 | 111112(*) |

|

|

|

|

|
| p6m (*632) | p3m1 (*333) | cmm (2*22) | p2 (2222) | p2 (2222) |
| 121213 | 111212 | 111112 | 121314 | 111213 |

|

|

|

|

|
| p31m (3*3) | p3 (333) | |||
Решётка A2 и упаковка кругов
[править | править код]
2 как три треугольные мозаики:


 +
+ 

 +
+ 


Расположение вершин[англ.] треугольной мозаики называется решёткой A2[4]. Она является 2-мерным вариантом симлектических сот[англ.].
Решётка A*
2 (которая также называется A3
2) может быть построена как объединение трёх решёток A2 и эквивалентна решётке A2.


 +
+ 

 +
+ 

 = dual of
= dual of 

 =
= 


Вершины треугольной мозаики являются центрами наиболее плотной упаковки кругов [5]. Любой круг соприкасается с 6 другими кругами (контактное число). Плотность упаковки равна , это около 90,69 %. Поскольку объединение трёх решёток A2 снова будет решёткой A2, круги можно раскрасить в три цвета.
Ячейкой диаграммы Вороного треугольной мозаики является шестиугольник, так что мозаика Вороного, шестиугольная мозаика, имеет прямое отношение к упаковке кругов.
| Решётка A2 упаковки кругов | Решётка A* 2 упаковки кругов |
|---|---|

|

|
Геометрические варианты
[править | править код]Треугольные мозаики могут быть идентичны {3,6} топологии правильной мозаики (6 треугольника в каждой вершине). Существует 5 вершинно транзитивных вариантов с одинаковыми гранями (транзитивных по граням[англ.]). С точки зрения симметрии все грани имеют одинаковый цвет, раскраска же на рисунках представляет положение в сетке[6].
-
Разносторонний треугольник
симметрия p2 -
Разносторонний треугольник
симметрия pmg -
Равнобедренный треугольник
симметрия cmm -
Прямоугольный треугольник
симметрия cmm -
Правильный треугольник
симметрия p6m
Связанные многогранники и мозаики
[править | править код]Плоские мозаики связаны с многогранниками. Располагая меньше треугольников в каждой вершине, получим незаполненное пространство, что позволяет согнуть в фигуру в пирамиду. Отсюда можно получить правильные многогранники: пять, четыре и три треугольника в вершине дают икосаэдр, октаэдр и тетраэдр соответственно.
Эта мозаика топологически связана (как часть последовательности) с правильными многогранниками с символами Шлефли {3,n}.
| Сферическая | Евклидова | Компактная гипербол. | Пара- компактная |
Некомпактная гиперболическая | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|
| 3.3 | 33 | 34 | 35 | 36 | 37 | 38 | 3∞ | 312i | 39i | 36i | 33i |
Эта мозаика топологически связана (как часть последовательности) с полуправильными многогранниками с конфигурацией граней Vn.6.6.
 V3.6.6 |
 V4.6.6 |
 V5.6.6 |
 V6.6.6 |
 V7.6.6[англ.] |
Построение Витхоффа из шестиугольных и треугольных мозаик
[править | править код]Подобно однородным многогранникам существует восемь однородных мозаик, базирующихся на правильных шестиугольных мозаиках (или на двойственных треугольных мозаиках).
Если нарисовать плитки исходных граней красным, исходные вершины (получившиеся на их месте многоугольники) жёлтым, а исходные рёбра (получившиеся на их месте многоугольники) синим, существует 8 форм, 7 из которых топологически различны. (Усечённая треугольная мозаика топологически идентична шестиугольной мозаике.)
| Однородные шестиугольные/треугольные мозаики | ||||||||
|---|---|---|---|---|---|---|---|---|
| Фундаментальные домены |
Симметрия: [6,3], (*632) | [6,3]+, (632) | ||||||
| {6,3} | t{6,3} | r{6,3} | t{3,6} | {3,6} | rr{6,3} | tr{6,3} | sr{6,3} | |

|

|

|

|

|

|

|

|

|
| Конфиг. | 63 | 3.12.12 | (6.3)2 | 6.6.6 | 36 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 |
| Треугольные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Витхофф | 3 | 3 3 | 3 3 | 3 | 3 | 3 3 | 3 3 | 3 | 3 | 3 3 | 3 3 | 3 | 3 3 3 | | | 3 3 3 | |||
| Коксетер | |||||||||||
| Рисунок Вершинная фигура |
 (3.3)3 |
 3.6.3.6 |
 (3.3)3 |
 3.6.3.6 |
 (3.3)3 |
 3.6.3.6 |
 6.6.6 |
3.3.3.3.3.3 | |||
Связанные правильные комплексные бесконечноугольники
[править | править код]Существует 4 правильных комплексных апейрогона[англ.], имеющих те же вершины шестиугольной мозаики. Рёбра правильных комплексных апейрогонов могут содержать 2 и более вершин. Правильные апейрогоны p{q}r имеют ограничение: 1/p + 2/q + 1/r = 1. Рёбра имеют p вершин и вершинные фигуры являются r- угольниками [7].
Первый апейрогон состоит из 2-рёбер, следующие два имеют треугольные рёбра, последний имеет перекрывающиеся шестиугольные рёбра.

|

|

|
|
| 2{6}6 или |
3{4}6 или |
3{6}3 или |
6{3}6 или |
|---|
Другие треугольные мозаики
[править | править код]Существуют также три мозаики Лавеса[англ.], состоящие из треугольников одного типа:
 Разделённая ромбическая[англ.] 30°-60°-90° прямоугольные треугольники |
 Разделённая квадратная 45°-45°-90° прямоугольные треугольники |
 триразделённая треугольная мозаика[англ.] 30°-30°-120° равнобедренные треугольники |
См. также
[править | править код]- Замощение
- Полиамонд
- Шестиугольная решётка
- Треугольные мозаичные соты[англ.]
- Симлектические соты[англ.]
- Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
- Список однородных мозаик[англ.]
- Isogrid[англ.] (структурное проектирование, использующее треугольную мозаику)
Примечания
[править | править код]- ↑ 1 2 Голомб, 1975, с. 147.
- ↑ Weisstein, Eric W. Dual Tessellation (англ.) на сайте Wolfram MathWorld.
- ↑ Grünbaum, Shephard, 1987, с. 102-107.
- ↑ The Lattice A2. Дата обращения: 26 марта 2017. Архивировано 25 февраля 2021 года.
- ↑ Critchlow, 1987, с. 74–75, pattern 1.
- ↑ Grünbaum, Shephard, 1987, с. 473-481.
- ↑ Coxeter, 1991, с. 111-112, 136.
Литература
[править | править код]- С.В. Голомб. Полимино = Polyominoes / Пер. с англ. В. Фирсова. Предисл. и ред. И. Яглома. — М.: Мир, 1975. — С. 147. — 207 с.
- B. Grünbaum, G.C. Shephard. Chapter 2.1: Regular and uniform tilings, Chapter 2.9 Archimedean and Uniform colorings // Tilings and Patterns. — New York: W. H. Freeman & Co., 1987. — С. 58—65,102—107. — ISBN 0-7167-1193-1.
- R. Williams. The Geometrical Foundation of Natural Structure: A Source Book of Design. — New York: Dover Publications, 1979. — С. 35. — ISBN 0-486-23729-X.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5. Архивная копия от 19 сентября 2010 на Wayback Machine
- H. S. M. Coxeter. Regular Complex Polytopes. — 2ed. — New York, Port Chester, Melbourne, Sydney: Cambridge University Press, 1991. — ISBN 0-521-39490-2.
- Keith Critchlow. Order in Space: A design source book. — New York: Thames & Hudson, 1987. — ISBN 0-500-34033-1.
Ссылки
[править | править код]- Weisstein, Eric W. Triangular Grid (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Regular tessellation (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Uniform tessellation (англ.) на сайте Wolfram MathWorld.
- Klitzing, Richard. 2D Euclidean tilings x3o6o - trat - O2
- Amit Patel. Grid Math: Square, Hexagon, Triangle. — Алгоритмы представления шестиугольной и треугольной сеток в компьютерных стратегических играх.
Для улучшения этой статьи желательно:
|












