Четырёхскатный повёрнутый бикупол (Cymdj~]vtgmudw hkf~jurmdw Qntrhkl)

Квадратный гиробикупол
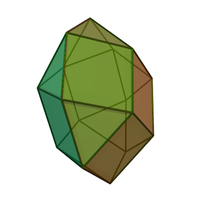Квадратный гиробикупол
Тип	Многогранник Джонсона J28 - J29 – J30
Свойства	выпуклый
Комбинаторика
Элементы	32 ребра 16 вершин
Грани	8 треугольников, 2 + 8 квадратов
Конфигурация вершины	8(3.4.3.4) 8(3.43)
Развёртка
Классификация
Группа симметрии	D4d

Четырёхскатный повёрнутый бикупол — один из многогранников Джонсона (J₂₉ = (по Залгаллеру) М₅+М₅). Подобно четырёхскатному прямому бикуполу (J₂₈ = 2М₅), он может быть получен соединением двух четырёхскатных куполов (J₄= М₅) по их основаниям. Разница лишь в том, что в этом многограннике половинки повёрнуты относительно друг друга на 45º.

Многогранник Джонсона — это один из 92 строго выпуклых многогранников, имеющих правильные грани, но не являющийся однородным (то есть, он не правильный, не архимедов, не призма или антипризма). Название многограннику дал Нортон Джонсон, который первым перечислил эти многогранники в 1966 .

Четырёхскатный повёрнутый бикупол является вторым в бесконечном множестве повёрнутых бикуполов.

С квадратным повёрнутым бикуполом связан удлинённый четырёхскатный повёрнутый бикупол. Этот многогранник получается, если вставить восьмиугольную призму между двумя половинками четырёхскатного повёрнутого бикупола. Есть споры, является ли удлинённый четырёхскатный повёрнутый бикупол архимедовым телом, поскольку, хотя многогранник удовлетворяет всем остальным требованиям, многогранник не вполне симметричен.

Формулы

Следующие формулы для объёма и площади поверхности могут быть использованы, если все грани являются правильными со стороной a :

$V=(2+{\frac {4{\sqrt {2}}}{3}})a^{3}\approx 3.88562...a^{3}$

$A=2(5+{\sqrt {3}})a^{2}\approx 13.4641...a^{2}$

Связанные многогранники и соты

Четырёхскатный повёрнутый бикупол образует заполняющие пространство соты с тетраэдрами, кубами и кубооктаэдрами.
Четырёхскатный повёрнутый бикупол образует заполняющие пространство соты с тетраэдрами, квадратными пирамидами и комбинацией из кубов, удлинённых четырёхугольных пирамид и удлинённых четырёхугольных бипирамид) .

Литература

• Norman W. Johnson. Convex polyhedra with regular faces (англ.) // Canadian Journal of Mathematics. — 1966. — Vol. 18. — P. 169–200. — doi:10.4153/cjm-1966-021-8.

Ссылки

• Eric W. Weisstein Square gyrobicupola (Johnson solid) Mathworld