Диэдр (:nz;j)

Множество правильных n-угольных диэдров
Множество правильных n-угольных диэдров
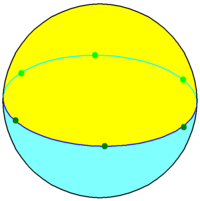	; Пример шестиугольного диэдра на сфере
Тип	правильный многогранник, сферическая мозаика
Комбинаторика
	n рёбер; n вершин
Грани	2 n-угольника
Конфигурация вершины	n.n
Двойственный многогранник	осоэдр
Классификация
Символ Шлефли	{n,2}
Символ Витхоффа[англ.]	2 \| n 2
Диаграмма Дынкина
Группа симметрии	Dnh, [2,n], (*22n), порядок 4n; Dn, [2,n]+, (22n), порядок 2n
	Медиафайлы на Викискладе

Диэдр — вид многогранника, состоящего из двух многоугольных граней, имеющих общий набор рёбер. В трёхмерном евклидовом пространстве он является вырожденным, если его грани плоские, в то время как в трёхмерном сферическом пространстве^[англ.] диэдр с плоскими гранями может рассматриваться как линза, примером которой является фундаментальная область линзового пространства L(p,q) ^[1].

Обычно правильный диэдр подразумевается состоящим из двух правильных многоугольников, и это даёт ему символ Шлефли {n,2}. Каждый многоугольник заполняет полусферу с правильным n-угольником на большом круге (экваторе) между ними ^[2].

Двойственным многогранником n-угольного диэдра является n-угольный осоэдр, в котором n двуугольных граней имеют две общие вершины.

Как многогранник

Диэдр можно считать вырожденной призмой, состоящей из двух (плоских) n-сторонних многоугольников, соединённых внутренними сторонами, так что результирующий объект имеет нулевую высоту.

Как мозаика на сфере

Как сферическая мозаика диэдр может существовать в невырожденном виде с n-сторонними гранями, покрывающими сферу. Каждая грань этого диэдра является полусферой с вершинами на большом круге. (Грань правильная, если вершины находятся на равном расстоянии друг от друга.)

Правильный многогранник {2,2} самодвойственен и является одновременно осоэдром и диэдром.

Правильные диэдры: (мозаики сферы)
Рисунок
Шлефли	{2,2}	{3,2}	{4,2}	{5,2}	{6,2}…
Коксетер
Грани	2 {2}	2 {3}	2 {4}	2 {5}	2 {6}
Рёбра и вершины	2	3	4	5	6

Бесконечноугольный диэдр

В пределе диэдр становится бесконечноугольным диэдром^[англ.] в виде 2-мерной мозаики:

Дитоп

Правильный дитоп — это n-мерный аналог диэдра с символом Шлефли {p, … q, r,2}. Дитоп имеет две (n-1)-мерной грани {p, … q, r}, которые имеют общую (n-12)-мерную грань.

См. также

Многогранник

Примечания

↑ Gausmann и др., 2001, с. 5155–5186.
↑ Coxeter, 1973, с. 12.

Литература

Evelise Gausmann, Roland Lehoucq, Jean-Pierre Luminet, Jean-Philippe Uzan, Jeffrey Weeks. Topological Lensing in Spherical Spaces // Classical and Quantum Gravity. — 2001. — Т. 18. — doi:10.1088/0264-9381/18/23/311. — arXiv:gr-qc/0106033.
Peter McMullen, Egon Schulte. Abstract Regular Polytopes. — 1st. — Cambridge University Press, 2002. — ISBN 0-521-81496-0.
H.S.M. Coxeter. Regular Polytopes. — 3rd. — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8.
Weisstein, Eric W. Dihedron (англ.) на сайте Wolfram MathWorld.

[_36a6171e34c4ff24-1] Gausmann и др., 2001, с. 5155–5186.

[_f72fc2b67a813c1e-2] Coxeter, 1973, с. 12.

[1]

[2]