Огранка (геометрия) (Kijgutg (iykbymjnx))
В геометрии огранка — это процесс удаления части многоугольника или многогранника без создания новых вершин.
Новые рёбра огранённого многогранника могут быть созданы вдоль диагоналей граней[англ.] или внутренних диагоналей[англ.]. Огранённый многогранник будет иметь две грани для каждого ребра и является новым многогранником или соединением многогранников.
Огранка является обратным или двойственным образованию звёздчатой формы. Для каждой звёздчатой формы некоторого выпуклого многогранника существует двойственная огранка двойственного многогранника.
Огранённые многоугольники
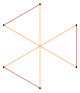
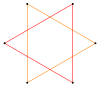
[править | править код]Например, правильный пятиугольник имеет одну симметричную огранку, пентаграммы, а правильный шестиугольник имеет две симметричные огранки, одна из них — многоугольник, а другая является соединением двух треугольников.
| Выпуклые | ||
|---|---|---|
| Правильный пятиугольник {5} |
Правильный шестиугольник {6} | |

|

| |
| Правильные | Квазиправильные | Правильные соединения |
| Пентаграмма {5/2} |
Звёздчатый шестиугольник | гексаграмма {6/2} |

|
|
|
Огранённые многогранники
[править | править код]Правильный икосаэдр может быть огранён до трёх правильных многогранников Кеплера — Пуансо — малого звёздчатого додекаэдра, большого додекаэдра и большого икосаэдра. Они имеют 30 рёбер.
| Выпуклые | Правильные звёзды | ||
|---|---|---|---|
| икосаэдр | Большой додекаэдр | Малый звёздчатый додекаэдр | Большой икосаэдр |

|

|

|

|
Правильный додекаэдр может быть огранён до одного правильного многогранника Кеплера — Пуансо, трёх однородных звёздчатых многогранников и трёх соединений многогранников. Однородные звёзды и соединение пяти кубов[англ.] строятся на диагоналях граней[англ.]. Выемчатый додекаэдр[англ.] является огранкой со звёздчатыми октаграммными гранями.
| Выпуклые | Правильные звёзды | Однородные звёзды | Вершинно транзитивные | ||
|---|---|---|---|---|---|
| додекаэдр | большой звёздчатый додекаэдр | Малый битригональный икосододекаэдр[англ.] | Битригональный додекаэдр[англ.] | Большой битигональный икосододекаэдр[англ.] | Выемчатый додекаэдр[англ.] |

|

|

|

|

|

|
| Выпуклые | Правильные соединения | ||
|---|---|---|---|
| додекаэдр | пять тетраэдров | пять кубов[англ.] | десять тетраэдров[англ.] |

|

|

|

|
История
[править | править код]Огранка изучалась не столь интенсивно, как образование звёздчатой формы.
- В 1619 году Кеплер описал правильное соединение двух тетраэдров, заключённых в куб, которое назвал Stella octangula. Похоже, это первый известный пример огранки.
- В 1858 году Бертран получил правильные звёздчатые многогранники (тела Кеплера — Пуансо) путём огранки правильных выпуклых икосаэдра и додекаэдра.
- В 1974 году Бридж перечислил несколько огранок правильных многогранников, включая огранки додекаэдра.
- В 2006 году Инчибальд описал базовую теорию диаграмм огранки для многогранников. Для заданной вершины диаграмма показывает возможные рёбра и фасеты (новые грани), которые могут быть использованы для огранки исходной оболочки. Эта диаграмма двойственна диаграмме образования звёздчатой формы двойственного многогранника, которая показывает все возможные рёбра и вершины для некоторой плоскости грани исходного ядра.
Примечания
[править | править код]Литература
[править | править код]- J. Bertrand. Note sur la théorie des polyèdres réguliers // Comptes rendus des séances de l'Académie des Sciences. — 1858. — Т. 46. — С. 79—82.
- N. J. Bridge. Facetting the dodecahedron // Acta crystallographica. — 1974. — Т. A30. — С. 548—552.
- G. Inchbald. Facetting diagrams // The mathematical gazette. — 2006. — Т. 90. — С. 253—261.
- Alan Holden. Shapes, Space, and Symmetry. — New York: Dover, 1991. — Т. 94.
Ссылки
[править | править код]- Weisstein, Eric W. Faceting (англ.) на сайте Wolfram MathWorld.
- Джордж Ольшевски Faceting на Glossary for Hyperspace
Для улучшения этой статьи желательно:
|