Гептеракт (Iyhmyjgtm)

Гептеракт
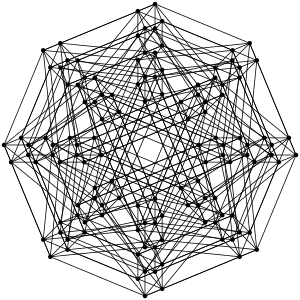
Тип	Правильный семимерный политоп
Символ Шлефли	{4,3,3,3,3,3}
6-мерных ячеек	14
5-мерных ячеек	84
4-мерных ячеек	280
Ячеек	560
Граней	672
Рёбер	448
Вершин	128
Вершинная фигура	Правильный 6-симплекс
Двойственный политоп	7-ортоплекс

Гептера́кт, также 7-куб или 7-гиперкуб, тетрадека-7-топ, тетрадекаэксон (тетрадекаэкзон) — аналог куба в семимерном пространстве.

Определяется как выпуклая оболочка 128 точек $[\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1]$.

Связанные политопы

Двойственное гептеракту тело — 7-ортоплекс, семимерный аналог октаэдра.

Если применить к гептеракту альтернацию (удаление чередующихся вершин), можно получить однородный семимерный многогранник, называемый полугептеракт, который является представителем семейства полугиперкубов.

Свойства

Если у гептеракта $a$ — длина ребра, то существуют следующие формулы для вычисления основных характеристик тела:

7-гиперобъём:

$V_{7}=a^{7}$

6-гиперобъём гиперповерхности:

$V_{6}(hypersurface)=14a^{6}$

Радиус описанной гиперсферы:

$R={\frac {a{\sqrt {7}}}{2}}$

Радиус вписанной гиперсферы:

$r={\frac {a}{2}}$

Состав

Гептеракт состоит из:

• 14 гексерактов,
• 84 пентеракта,
• 280 тессерактов,
• 560 кубов или ячеек,
• 672 квадрата или граней,
• 448 отрезков или рёбер,
• 128 точек или вершин.

Визуализация

Гептеракт можно визуализировать либо параллельным, либо центральным проецированием. В первом случае обычно применяется косоугольная параллельная проекция, которая представляет собой 2 равных гиперкуба размерности n-1, один из которых может быть получен в результате параллельного переноса второго (для гептеракта это 2 гексеракта), вершины которых попарно соединены. Во втором случае обычно используют диаграмму Шлегеля, которая выглядит как гиперкуб размерности n-1, вложенный в гиперкуб той же размерности, у которых вершины также попарно соединены (для гептеракта проекция представляет собой гексеракт, вложенный в другой гексеракт).

Изображения

Проекция вращения гептеракта

Ссылки

• Кокстер, Правильные политопы, (третье издание, 1973), Dover edition, ISBN 0-486-61480-8
• Джордж Ольшевски. Glossary for Hyperspace (Словарь терминов многомерной геометрии)