Окружность (Ktjr'ukvm,)

Окружность (C), её центр (O), радиус (R) и диаметр (D)

Сектор и сегмент круга и дуга окружности

Построение окружности циркулем

Практическое построение окружности возможно с помощью циркуля. Окру́жность — замкнутая плоская кривая, все точки которой равноудалены от заданной точки, лежащей в той же плоскости, что и кривая: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность), в зависимости от подхода, круг может включать или не включать.

Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.

Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Далее всюду буква $R$ обозначает радиус окружности.

Хорды, дуги и касательные

Хорды и дуги

• 
  1 — секущая, 2 — хорда AB (отмечена красным), 3 — сегмент (отмечен зелёным), 4 — дуга
• 
  Секторы круга

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: $D=2R,$ он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды.

Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки).

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Для заданной окружности имеют место следующие свойства.

• Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
• Равным хордам соответствуют равные дуги, и наоборот.

Взаимное расположение прямой и окружности

Касательная и секущая

Если расстояние от центра окружности до прямой равно радиусу, то прямая и окружность имеют одну общую точку, которая называется точкой касания. Такая прямая называется касательной к окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведённому в точке касания. То есть радиус является одновременно и нормалью к окружности.

Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Если расстояние от центра окружности до прямой меньше радиуса, то прямая пересекает окружность в двух точках и называется секущей.

Если расстояние от центра окружности до прямой больше радиуса, то окружность и прямая не имеют точек пересечения.

Углы

• 
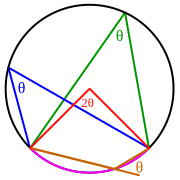
  Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)
• 
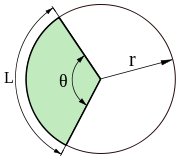
  К расчёту длины дуги и хорды

Центральный угол — угол с вершиной в центре окружности. Вписанный угол — угол, вершина которого принадлежит окружности, а стороны пересекают эту окружность. Говорят, что центральный или вписанный углы опираются на дугу, высекаемую на окружности их лучами, или же на хорду, стягивающую эту дугу.

Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.

Из определения радиана следует, что длина $L$ любой дуги окружности связана с центральным углом $\theta$, опирающимся на эту дугу, простым соотношением: $L=R\theta ,$ при этом длина хорды, стягивающей ту же дугу, равна $2R\sin {\theta \over 2}<L.$ Поскольку длина окружности равна $2\pi R$, с ростом угла значение его радианной меры меняется от 0 до $2\pi .$

Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.

Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.

Свойства вписанных углов:

• Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
• Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
• Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

Другие свойства:

• Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
• Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
• Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.

Свойства

• Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
• Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
• Говорят, что две окружности касаются, если они имеют единственную общую точку. Точка касания двух окружностей лежит на прямой, проходящей через их центры.

$AE\cdot EB=CE\cdot ED$

• Теорема о секущих: Если через произвольную точку $E$ проведена секущая, то произведение расстояний от этой точки до точек пересечения секущей с окружностью не зависит от выбора секущей (и равно абсолютной величине степени точки относительно окружности). Если точка $E$ лежит вне окружности, то из неё к окружности можно провести касательную. Квадрат длины отрезка касательной до точки касания будет равен той же величине.

• Как частный случай предыдущего, при пересечении двух хорд в произвольной точке $E$ получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рисунок), то есть $AE\cdot EB=CE\cdot ED$.

Формулы

Если радиус круга равен 1, то его окружность равна 2π.

Длина окружности:

$C=2\pi R=\pi D$

Радиус окружности:

$R={\frac {C}{2\pi }}={\frac {D}{2}}$

Диаметр окружности:

$D={\frac {C}{\pi }}=2R$

Площадь круга радиуса R:

$S=\pi R^{2}={\frac {\pi D^{2}}{4}}$

Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:

$S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}$

Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:

$S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}-{\frac {R^{2}\sin \alpha }{2}}$

История

Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.

Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.

Окружность получается как сечение конуса плоскостью, перпендикулярной его оси

Аналитическая геометрия окружностей

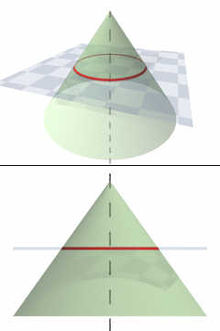
С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.

Декартовы координаты

Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)

Общее уравнение окружности записывается как:

$x^{2}+y^{2}+Ax+By+C=0,$

или

$\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},$

где

$2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.$

Точка $\left(x_{0},y_{0}\right)$ — центр окружности, $R$ — её радиус.

Уравнение окружности радиуса $R$ с центром в начале координат:

$x^{2}+y^{2}=R^{2}.$

Уравнение окружности, проходящей через точки $\left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right),$ не лежащие на одной прямой (с помощью определителя):

${\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.$

Тогда в явном виде координаты центра окружности определяются по формулам:

$x_{0}=-{\frac {1}{2}}{\frac {y_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+y_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+y_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}$

$y_{0}={\frac {1}{2}}{\frac {x_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+x_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+x_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}$

Окружность также можно описать с помощью параметрического уравнения:

${\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leqslant \varphi <2\pi .$

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

$y=y_{0}\pm {\sqrt {R^{2}-(x-x_{0})^{2}}}.$

Если центр окружности совпадает с началом координат, функции принимают вид:

$y=\pm {\sqrt {R^{2}-x^{2}}}.$

Полярные координаты

Окружность радиуса $R$ с центром в точке $\left(\rho _{0},\phi _{0}\right)$:

$\rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.$

Если полярные координаты центра окружности $\rho _{0}=R,\;\phi _{0}=\alpha ,$ то проходящая через начало координат окружность описывается уравнением:

$\rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leqslant \varphi \leqslant \alpha +{\frac {\pi }{2}}.$

Если же центр является началом координат, то уравнение будет иметь вид

$\rho =R.$

Подерные координаты

Окружность радиуса $R$ с центром в полюсе:

$pR=r^{2}.$

Комплексная плоскость

На комплексной плоскости окружность задаётся формулой:

$\left|z-z_{0}\right|=R,\,R\in \mathbb {R}$

или в параметрическом виде

$z=z_{0}+Re^{it},\,R,t\in \mathbb {R} .$

В частном случае, когда начало координат лежит на окружности:

$z=R+Re^{it},\,R,t\in \mathbb {R} .$.

Если окружность единичная, $R=1,$ то соответственно:

$z=z_{0}+e^{it},\,t\in \mathbb {R} ,$

$z=1+e^{it},\,t\in \mathbb {R} .$.

Окружности в пространстве

В пространстве окружность радиуса $R$ с центром в точке $M_{0}(x_{0},y_{0},z_{0})$ можно определить как контур диаметрального сечения сферы

$(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2}$

плоскостью

$a\cdot (x-x_{0})+b\cdot (y-y_{0})+c\cdot (z-z_{0})=0$,

где $a,b,c$ — параметры, не равные одновременно нулю; то есть все точки, лежащие на данной окружности, есть решения системы

${\begin{cases}(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},\\a{\cdot }(x-x_{0})+b{\cdot }(y-y_{0})+c{\cdot }(z-z_{0})=0.\end{cases}}$

Например, когда $a$ и $c$ не равны нулю одновременно, решения этой системы можно задать параметрически следующим образом:

${\begin{cases}x=x_{0}+{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(c\cdot \cos t-{\dfrac {a\cdot b\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\\[10pt]y=y_{0}+{\dfrac {R\cdot {\sqrt {a^{2}+c^{2}}}}{\sqrt {a^{2}+b^{2}+c^{2}}}}\cdot \sin t,\\[10pt]z=z_{0}-{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(a\cdot \cos t+{\dfrac {b\cdot c\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\end{cases}}t\in [0;2\pi ).$

Ось окружности в пространстве — перпендикуляр, восстановленный к плоскости окружности в её центре.

Касательные и нормали

Уравнение касательной к окружности в точке $\left(x_{1},y_{1}\right)$ определяется уравнением

$\left({\frac {A}{2}}+x_{1}\right)x+\left({\frac {B}{2}}+y_{1}\right)y+\left({\frac {A}{2}}x_{1}+{\frac {B}{2}}y_{1}+C\right)=0.$

Уравнение нормали в той же точке можно записать как

${\frac {x-x_{1}}{2x_{1}+A}}={\frac {y-y_{1}}{2y_{1}+B}}.$

Концентрические окружности

Концентрические окружности

Окружности с общим центром, но разными радиусами, называются концентрическими. Две окружности, заданные уравнениями:

$x^{2}+y^{2}+A_{1}x+B_{1}y+C_{1}=0,\;\;\;x^{2}+y^{2}+A_{2}x+B_{2}y+C_{2}=0$

являются концентрическими в том и только в том случае, когда $A_{1}=A_{2}$ и $B_{1}=B_{2}.$

Дополнительные сведения

Определение треугольников для одной окружности

Через вершину треугольника проведена касательная к описанной окружности

• Треугольник ABC называется вписанным в окружность (A,B,C), если все три его вершины A, B и C лежат на этой окружности. При этом окружность называется описанной окружностью треугольника ABC (См. Описанная окружность).
• Касательная к окружности, проведённая через любую вершину вписанного в неё треугольника, антипараллельна стороне треугольника, противоположной данной вершине.
• Треугольник ABC называется описанным около окружности (A',B',C'), если все три его стороны AB, BC и CA касаются этой окружности в некоторых точках соответственно C' , A' и B' . При этом окружность называется вписанной окружностью треугольника ABC (См. Вписанная окружность).
• Треугольник ABC называется внеописанным для окружности (A',B',C'), если все 3 его стороны AB, BC и CA касаются этой окружности в некоторых точках соответственно C' , A' и B' , а именно: одной из 2 сторон касается непосредственно, а также продолжений 2 других сторон за пределы треугольника. При этом окружность называется вневписанной окружностью треугольника ABC (См. Вневписанная окружность).

Варианты определения окружности

• Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом (Определение через угол, опирающийся на диаметр окружности).
• Окружность с хордой AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под постоянным углом с одной стороны, равным вписанному углу дуги AB, и под другим постоянным углом с другой стороны, равным 180 градусов минус вписанный угол дуги AB, указанный выше (Определение через вписанный угол).
• Фигура состоящая из таких точек $X,$ что отношение длин отрезков AX и BX постоянно: ${\frac {AX}{BX}}=c\neq 1,$ является окружностью (Определение через окружность Аполлония).
• Фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками, также является окружностью (Определение через теорему Пифагора для произвольного прямоугольного треугольника, вписанного в окружность, с гипотенузой, являющейся диаметром окружности).
• Окружность — замкнутая, самонепересекающаяся фигура, обладающая следующим свойством. Если через произвольную точку E внутри неё провести любые хорды AB, CD, GF и т. д., тогда справедливы равенства: $AE\cdot EB=CE\cdot ED=GE\cdot EF$ (см. рис.). Равенства всегда будут выполняться независимо от выбора точки E и направлений проведённых через неё хорд (Определение через пересекающиеся хорды).

$AE\cdot EB=CE\cdot ED$

• Окружность — замкнутая, самонепересекающаяся фигура, обладающая следующим свойством. Если через произвольную точку M вне её провести две касательные до точек их касания с окружностью, например, A и B, тогда их длины всегда будут равны: $MA=MB$. Равенство всегда будет выполняться независимо от выбора точки M (Определение через равные касательные).
• Окружность — замкнутая, самонепересекающаяся фигура, обладающая следующим свойством. Отношение длины любой её хорды к синусу любого её вписанного угла, опирающегося на эту хорду, есть величина постоянная, равная диаметру этой окружности (Определение через теорему синусов).
• Окружность — это частный случай эллипса, у которого расстояние между фокусами равно нулю (Определение через вырожденный эллипс).
• Окружность есть Синусоидальная спираль при $n=1$.

Связанные определения для двух окружностей

• Две окружности, имеющие общий центр, называются концентрическими.
• Две окружности, имеющие лишь одну общую точку, называются касающимися внешним образом, если их круги не имеют других общих точек, и внутренним образом, если их круги лежат один внутри другого.
• Две окружности, имеющие две общие точки, называются пересекающимися. Их круги (ими ограниченные) пересекаются по области, называемой двойным круговым сегментом.
• Углом между двумя пересекающимися (или касающимися) окружностями называется угол между их касательными, проведёнными в общей точке пересечения (или касания).
• Также углом между двумя пересекающимися (или касающимися) окружностями можно считать угол между их радиусами (диаметрами), проведёнными в общей точке пересечения (или касания).
• Поскольку для любой окружности её радиус (или диаметр) и касательная, проведённые через любую точку окружности, взаимно перпендикулярны, то радиус (или диаметр) можно считать нормалью к окружности, построенной в данной её точке. Следовательно, два типа углов, определённых в двух предыдущих двух пунктах, всегда будут равны между собой, как углы со взаимно перпендикулярными сторонами.
• Радикальная ось двух окружностей — геометрическое место точек, степени которых относительно двух заданных окружностей равны. Иными словами, равны длины четырёх касательных, проведённых к двум данным окружностям из любой точки M данного геометрического места точек.

Определения углов для двух окружностей

• Угол между двумя пересекающимися окружностями — угол между касательными к окружностям в точке пересечения этих окружностей. Оба угла между двумя пересекающимися окружностями равны.
• Угол между двумя непересекающимися окружностями — угол между двумя общими касательными к двум окружностям, образуемый в точке пересечения этих двух касательных. Точка пересечения этих двух касательных должна лежать между двумя окружностями, а не со стороны одной из них (этот угол не рассматривается). Оба вертикальных угла между двумя непересекающимися окружностями равны.

Ортогональность (перпендикулярность)

Ортогональные окружности

Две окружности, пересекающиеся под прямым углом, называются ортогональными (перпендикулярными). Две окружности, заданные уравнениями:

$x^{2}+y^{2}+A_{1}x+B_{1}y+C_{1}=0,\;\;\;x^{2}+y^{2}+A_{2}x+B_{2}y+C_{2}=0$

являются ортогональными тогда и только тогда, когда выполняется условие:

$A_{1}A_{2}+B_{1}B_{2}=2\left(C_{1}+C_{2}\right).$

Другими словами, две пересекающиеся в точках A и B окружности с центрами O и O' называются ортогональными, если являются прямыми углы OAO' или OBO' . Именно это условие гарантирует прямой угол между окружностями. В этом случае перпендикулярны радиусы (нормали) двух окружностей, проведённые в точку их пересечения. Следовательно, перпендикулярны и касательные двух окружностей, проведённые в точку их пересечения. Касательная окружности перпендикулярна радиусу (нормали), проведённому в точку касания. Обычно угол между кривыми — это угол между их касательными, проведёнными в точке их пересечения.

• Возможно другое дополнительное условие. Пусть две пересекающиеся в точках A и B окружности имеют середины пресекающихся дуг в точках C и D, то есть дуга AС равна дуге СB, дуга AD равна дуге DB. Тогда эти окружности называются ортогональными, если являются прямыми углы CAD и CBD.
• В теории инверсии вводятся: окружность или прямая, перпендикулярные к окружности $\Gamma$. При этом перпендикулярность определяется также, как и выше.
• В теории инверсии прямая перпендикулярна к окружности $\Gamma$, если она проходит через центр последней.

Связанные определения для трёх окружностей

• Три окружности называются взаимно касающимися (пресекающимися), если любые две из них касаются (пресекаются) друг друга.
• В геометрии радикальный центр трёх окружностей — это точка пересечения трёх радикальных осей пар окружностей. Если радикальный центр лежит вне всех трёх окружностей, то он является центром единственной окружности (радикальной окружности), которая пересекает три данные окружности ортогонально.

Лемма Архимеда

Лемма Архимеда. Если окружность вписана в сегмент окружности, стягиваемый хордой $BC$, и касается дуги в точке $A_{1}$, а хорды — в точке $A_{2}$, то прямая $A_{1}A_{2}$ является биссектрисой угла $BA_{1}C$. Лемма Архимеда играет важную роль при построении изоциркулярного преобразования.

Доказательство

Пусть $G$ — гомотетия, переводящая малую окружность в большую. Тогда ясно, что $A_{1}$ является центром этой гомотетии. Тогда прямая $BC$ перейдёт в какую-то прямую $a$, касающуюся большой окружности, а $A_{2}$ перейдёт в точку на этой прямой и принадлежащей большой окружности. Вспомнив, что гомотетия переводит прямые в параллельные им прямые, понимаем, что $a\parallel BC$. Пусть $G(A_{2})=A_{3}$ и $D$ — точка на прямой $a$, такая, что $\angle CA_{3}D$ — острый, а $E$ — такая точка на прямой $a$, что $\angle BA_{3}E$ — острый. Тогда, так как $a$ — касательная к большой окружности $\angle CA_{3}D$$=$$\angle CBA_{3}$$=\angle BA_{3}E=\angle BCA_{3}$. Следовательно $\bigtriangleup BCA_{3}$ — равнобедренный, а значит $\angle BA_{1}A_{3}=\angle CA_{1}A_{3}$, то есть $A_{1}A_{2}$ — биссектриса угла $\angle BA_{1}C$.

Теорема Декарта для радиусов четырёх попарно касающихся окружностей

Основная статья: Теорема Декарта (геометрия)

Теорема Декарта утверждает, что радиусы любых четырёх взаимно касающихся окружностей удовлетворяют некоторому квадратному уравнению. Их иногда называют окружностями Содди.

Преобразования окружности

Антигиперболизм окружности

Основная статья: Грушевидная квартика

Пять форм грушевидной квартики $x^{4}-2ax^{3}=-b^{2}y^{2}.$ Из них фиолетовая - волчок, красная — квартика Бонне, синяя — с тройной вершиной

Грушеви́дная кварти́ка (англ. piriform quartic, от лат. pirum — плод груши и лат. quartus — четвёртый; англ. pear-shaped quartic; pear-shaped curve) — антигиперболизм окружности с полюсом на этой окружности и прямой, перпендикулярной диаметру окружности с концом на полюсе.

В декартовых координатах грушевидная квартика — это антигиперболизм окружности

$(x-a)^{2}+y^{2}=a^{2}$

с радиусом $a$ и полюсом в начале координат на окружности и прямой $x=b$, имеющий следующее уравнение:

$(x-a)^{2}+\left(b{\frac {y}{x}}\right)^{2}=a^{2},$

или

$x^{4}-2ax^{3}=-b^{2}y^{2};$

или

$y=\pm {\frac {x}{b}}{\sqrt {2ax-x^{2}}}.$

Полагают, что $a\neq 0$ и $b\neq 0$:

• при $a=0$ грушевидная квартика вырождается в точку $(0,\,0);$
• при $b=0$ грушевидная квартика вырождается в две прямые $x=0$ и $x=2a.$

Относится к плоским алгебраически кривым 4-го порядка.

Грушевидная квартика — это кривая, обладающая следующими простыми свойствами:

• ограниченная и замкнутая;
• связная;
• имеет одну особую точку — касп;
• имеет одну ось симметрии.

Базовая окружность есть гиперболизм грушевидной квартики.

Грушевидную квартику изучали английский математик Джон Валлис в 1685 году, французский математик Пьер Бонне в 1844 году и французский математик Гастон Сели-Лонгшан в 1886 году.

Гиперболизм окружности

Основная статья: Аньезиана

Пять форм аньезианы $y(b^{2}+x^{2})=2ab^{2}.$ Из них оранжевая - верзиера, красная — псевдоверзиера

Аньезиа́на (англ. agnesiana — кривая Аньези) (частный случай — верзие́ра) — гиперболизм окружности с полюсом на этой окружности и произвольной прямой, перпендикулярной диаметру окружности с концом на полюсе.

В декартовых координатах аньезиана — это гиперболизм окружности

$x^{2}+(y-a)^{2}=a^{2}$

с радиусом $a$ и полюсом в начале координат на окружности и прямой $y=b$, имеющий следующее уравнение:

$\left(x{\frac {y}{b}}\right)^{2}+(y-a)^{2}=a^{2},$

или

$y(b^{2}+x^{2})=2ab^{2};$

или

$y={\frac {2ab^{2}}{b^{2}+x^{2}}}.$

Полагают, что $a>0$: при $a=0$ аньезиана вырождается в ось абсцисс.

Относится к плоским алгебраически кривым 3-го порядка.

Аньезиана — это кривая, обладающая следующими простыми свойствами:

• неограниченная;
• имеет одну асимптоту.
• связная;
• имеет бесконечно удалённую изолированную точку в направлении оси ординат;
• особых точек нет;
• имеет одну ось симметрии.

Образующая окружность есть антигиперболизм аньезианы.

Своё название аньезиана получила в честь итальянского математика Марии Гаэтаны Аньези, исследовавшей частный случай этой кривой — верзиеру — в 1748 году. Ранее верзиеру изучали Пьер Ферма в 1630 году и Гвидо Гранди в 1703 году.

Конхоида окружности

Основная статья: Улитка Паскаля

Семь форм улиток Паскаля как конхоиды чёрной окружности с полюсом (0, 0): $r(\varphi )=2a\cos \varphi +l.$ Из них красная — с параболической точкой распрямления, зелёная — кардиоида, синяя — трисектриса

Страница книги Дюрера 1525 года с линией паука (Spinnenlinie)

Ули́тка Паска́ля (англ. limacon of Pascal, от лат. limax — улитка) ― конхоида окружности с полюсом на этой окружности.

Обычно представляется следующим уравнением конхоиды окружности в полярной системе координат:

$r(\varphi )=2a\cos \varphi +l,$

где $a$ — радиус базовой окружности конхоиды; $l$ — приращение радиус-вектора окружности, проведённого из полюса конхоиды на окружности.

Относится к плоским алгебраически кривым 4-го порядка.

Улитка Паскаля — это кривая, обладающая следующими простыми свойствами:

• ограниченная и замкнутая;
• связная только для кардиоиды и улитки с петлёй, остальные кривые имеют изолированную точку;
• имеет одну особую точку — двойную: точку самопересечения, касп или изолированную в зависимости от параметров;
• имеет одну ось симметрии.

Названа по имени французского учёного Этьена Паскаля (отца Блеза Паскаля), рассмотревшего её в первой половине XVII века. Улитка Паскаля изучалась Альбрехтом Дюрером в 1525 году под названием арахна (линия паука) (англ. Arachne; нем. Spinnenlinie; фр. arachnée), Этьеном Паскалем в 1630 году и Жилем Робервалем, который и назвал кривую «улиткой Паскаля» в 1650 году.

Подера окружности

Обзорная статья: Подера

При подерных преобразованиях окружности относительно разных полюсов могут получиться следующие подеры:

• сама эта окружность относительно полюса подеры в центре окружности;
• кардиоида относительно полюса подеры на окружности;
• улитка Паскаля (не кардиоида) относительно остальных положений полюса подеры.

• Подеры окружности
• 
  Улитка Паскаля — полюс подеры вне окружности
• 
  Кардиоида — полюс подеры на окружности
• 
  Улитка Паскаля — полюс подеры внутри окружности, но не в её центре

Полярное преобразование окружности

Обзорная статья: Полярное преобразование кривой

Гипербола — полярное преобразование окружности

При полярном преобразовании окружности получается гипербола, как показано на рисунке справа.

Подставим комплексное параметрическое уравнение окружности с центром $z_{0}$

$z(t)=z_{0}+Re^{it},\,R,t\in \mathbb {R} .$

в комплексное параметрическое уравнение полярного преобразования произвольной кривой

$Z(t)={\frac {2z'(t)}{{\overline {z(t)}}z'(t)-z(t){\overline {z'(t)}}}}.$

получаем комплексное параметрическое уравнение полярного преобразования окружности, то есть комплексное параметрическое уравнение гиперболы:

$Z(t)={\frac {2Rie^{it}}{(z_{0}+Re^{-it})Rie^{it}+(z_{0}+Re^{it})Rie^{-it}}}=$

${}={\frac {2e^{it}}{(z_{0}+Re^{-it})e^{it}+(z_{0}+Re^{it})e^{-it}}}=$

${}={\frac {2e^{it}}{z_{0}(e^{it}+e^{-it})+2Re^{-it}e^{it}}}=$

${}={\frac {e^{it}}{z_{0}\cos t+R}}.$

Эвольвента окружности

Анимация построения эвольвенты окружности

Основная статья: Эвольвента окружности

Эвольвентой окружности является траектория любой точки прямой линии, перекатываемой по окружности без скольжения. По эвольвенте обрабатывают профиль зубьев зубчатых колёс. Эвольвенту окружности можно получить, сматывая натянутую нить с цилиндрической поверхности. Конец этой нити будет описывать эвольвенту.

Движение по окружности

Основная статья: Круговое движение

В физике кругово́е движе́ние — это вращательное движение материальной точки или тела, когда ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела. В этом случае траектория точки или тела является окружностью, круговой орбитой. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение.

Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма.

Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона.

Ориентированная окружность

Основная статья: Аналлагматическая геометрия § Направленная окружность и направленная прямая

Обзорная статья: Ориентация

Ориентированная, или направленная, окружность, или цикл, — окружность, для которой окончательно выбрано одно из двух направлений.

Две ориентированные окружности касаются, если их направления в общей точке совпадают. Ориентированная окружность и ориентированная прямая касаются, если их направления в общей точке совпадают.

На следующем рисунке показаны:

• касающиеся ориентированные окружности;
• не касающиеся ориентированные окружности, которые касаются как обычные окружности.

• Касание направленных окружностей
• 
  Касающиеся ориентированные окружности
• 
  Не касающиеся ориентированные окружности, касающиеся как обычные окружности

Многомерное обобщение

Обобщённую окружность можно определить для любой математической структуры, где задано понятие расстояния. В частности, обобщением для многомерного евклидова пространства является гиперсфера; в трёхмерном пространстве это обычная сфера. В сферической геометрии важную роль играют окружности на сфере, центр которых совпадает с центром сферы («большие круги»).

В культуре и мистике

Джон Уильям Уотерхаус. Магический круг (1886). Британская галерея Тейт, Лондон

Окружность, наряду с близкими понятиями круга, кольца и сферы, с глубокой древности считалась божественным символом высшего совершенства, символом красоты и равенства. Античные астрономы были убеждены, что небесные светила размещены на вращающихся сферах и, таким образом, движутся по окружностям. Рыцари короля Артура сидели за круглым столом, что подчёркивало их равноправие.

В египетской мифологии бог-творец Хнум вылепил людей на гончарном круге. В Книге Притчей Соломоновых говорится, что при сотворении мира Бог «проводил круговую черту по лицу бездны» (Прит. 8:27). Для защиты от «нечистой силы» полагалось очертить вокруг себя окружность (магический круг). На изображениях христианских святых их лица окружены круглым нимбом. Преисподняя во многих религиях состоит из концентрических кругов, что символизирует безысходность. В Стоунхендже и других кромлехах камни расставлены по окружности.

В различных мистических доктринах окружность часто символизирует бесконечность и цикличность существования (уроборос, Сансара), равновесие (инь/ян), стабильность и др.. Похожий смысл усматривается в идиомах и поговорках многих народов, например: «круглый год», «круг общения», «порочный круг», «круговая порука» и т. п. Вероятно, широко распространённый обычай обмениваться кольцами между женихом и невестой символизирует вечность чувств, устойчивость семьи.

Окружность используется в графике многих символов, например, в знаке пацифизма, символе охраны авторского права (©) и т. д.

См. также

• Глоссарий планиметрии: О
• Вневписанная окружность
• Вписанная и вневписанные в треугольник окружности
• Вписанные и описанные фигуры для треугольника
• Вписанная окружность
• Описанная окружность
• Циклоида
• 360° (значения)

Литература

• Атанасян Л. С., Бутузов В. Ф.. и др. Дополнительные главы к учебнику 8 класса // Геометрия. — 3-е издание. — М.: Вита-Пресс, 2003.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 70.
• Маркушевич А. И. Замечательные кривые, выпуск 4. — М.: Гостехиздат, 1952. — 32 с. Архивная копия от 14 сентября 2008 на Wayback Machine
• Окружность // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4.
• Аньези локон // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1970. Т. 2. Ангола — Барзас. 1970. 632 с. с илл., 32 л. илл., 14 л. карт. С. 115.
• Аньези локон // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 75.
• Выгодский М. Я. Справочник по высшей математике. М.: АСТ: Астрель, 2006. 991 с., ил. ISBN 5-17-012238-1 (ООО «Издательство ACT»). ISBN 5-271-03651-0 (ООО «Издательство Астрель»).
• Иванов А. Б. Аньези локон // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 1 А—Г. М.: «Советская Энциклопедия», 1977. 1152 стб., ил. Стб. 297.
• Квартика // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 266.
• Линия // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1973. Т. 14. Куна — Ломами. 1973. 624 с. с илл., 32 л. илл., 6 л. карт. С. 466—470.
• Паскаля улитка // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 452.
• Розенфельд Б. А. Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики, книга четвёртая — геометрия / Гл. ред. П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. Ред. книги 4: В. Г. Болтянский, И. М. Яглом. М.: Физматгиз, 1963. 568 с., ил. С. 518—557.
• Савелов А. А. Плоские кривые. Систематика, свойства, применения. (Справочное руководство) / Под ред. А. П. Нордена. М.: Физматлит, 1960. 293 с., ил.
• Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка. М.: Физматлит, 1961. 271 с., ил.
• Соколов Д. Д. Паскаля улитка // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 4 Ок—Сло. М.: «Советская Энциклопедия», 1984. 1216 стб., ил. Стб. 226—227.
• Улитка Паскаля // Энциклопедический словарь / Гл. ред. Б. А. Введенский, т. 3 Пращур—Яя. М.: «Большая Советская энциклопедия», 1955. 744 с., ил. С. 472—473.
• Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве. Справочник с приложенипем дискеты «Плоские кривые». М.: ФАЗИС, 1997. 334 с., ил. ISBN 5-7036-0027-8.
• Яглом И. М. Окружности // Энциклопедия элементарной математики, книга четвёртая — геометрия / Гл. ред. П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. Ред. книги 4: В. Г. Болтянский, И. М. Яглом. М.: Физматгиз, 1963. 568 с., ил. С. 448—517.
• Яглом И. М., Атанасян Л. С. Геометрические преобразования // Энциклопедия элементарной математики, книга четвёртая — геометрия / Гл. ред. П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. Ред. книги 4: В. Г. Болтянский, И. М. Яглом. М.: Физматгиз, 1963. 568 с., ил. С. 49—158.
• Albrecht Dürer Underweysung der Messung, 1525.
• Ferréol Robert. Limaçon (or snail) of Pascal // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 12 января 2024 на Wayback Machine
• Ferréol Robert. Piriform quartic // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 28 февраля 2024 на Wayback Machine
• Ferréol Robert. Witch of Agnesi // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 25 августа 2023 на Wayback Machine
• Alfred Gray. Modern differential geometry of curves and surfaces with Mathematica. Third Edition by Elsa Abbena and Simon Salamon. Studies in Advanced Mathematics: Chapman and Hall/CRC, 2006. 982 p.
• Lawrence J. D. A Catalog of Special Plane Curves. New York: Dover Publications, Inc., 1972. 218 p.
• jan wassenaar limaçon // mathematical curves Архивная копия от 23 июля 2023 на Wayback Machine
• jan wassenaar piriform // mathematical curves Архивная копия от 29 ноября 2022 на Wayback Machine
• Weisstein Eric W. Limaçon // Wolfram MathWorld Архивная копия от 6 ноября 2020 на Wayback Machine
• Weisstein Eric W. Pear-Shaped Curve // Wolfram MathWorld Архивная копия от 19 декабря 2022 на Wayback Machine
• Weisstein Eric W. Piriform Curve // Wolfram MathWorld Архивная копия от 21 августа 2023 на Wayback Machine
• Weisstein Eric W. Witch of Agnesi // Wolfram MathWorld Архивная копия от 8 мая 2022 на Wayback Machine
• Zwikker C. The Advanced Geometry of Plane Curves and Their ApplicationsThe Advanced Geometry of Plane Curves and Their Applications. New York: Dover Publications, Inc., 1963. 299 p. ISBN 0486610780. ISBN 9780486610788.

Ссылки

• Окружность Архивная копия от 8 мая 2017 на Wayback Machine на www.univer.omsk.su.
• Круг и окружность Архивная копия от 17 марта 2017 на Wayback Machine на сайте Метмат (методика преподавания математики).