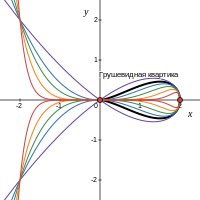
Грушевидная квартика (Ijroyfn;ugx tfgjmntg)

Обзорная статья: Окружность

Не следует путать с аньезианой — гиперболизмом окружности.

Пять форм грушевидной квартики $x^{4}-2ax^{3}=-b^{2}y^{2}.$ Из них фиолетовая - волчок, красная — квартика Бонне, синяя — с тройной вершиной

Грушеви́дная кварти́ка (англ. piriform quartic, от лат. pirum — плод груши и лат. quartus — четвёртый; англ. pear-shaped quartic; pear-shaped curve) — антигиперболизм окружности с полюсом на этой окружности и прямой, перпендикулярной диаметру окружности с концом на полюсе.

В декартовых координатах грушевидная квартика — это антигиперболизм окружности

$(x-a)^{2}+y^{2}=a^{2}$

с радиусом $a$ и полюсом в начале координат на окружности и прямой $x=b$, имеющий следующее уравнение:

$(x-a)^{2}+\left(b{\frac {y}{x}}\right)^{2}=a^{2},$

или

$x^{4}-2ax^{3}=-b^{2}y^{2};$

или

$y=\pm {\frac {x}{b}}{\sqrt {2ax-x^{2}}}.$

Полагают, что $a\neq 0$ и $b\neq 0$:

• при $a=0$ грушевидная квартика вырождается в точку $(0,\,0);$
• при $b=0$ грушевидная квартика вырождается в две прямые $x=0$ и $x=2a.$

Относится к плоским алгебраически кривым 4-го порядка.

Грушевидная квартика — это кривая, обладающая следующими простыми свойствами:

• ограниченная и замкнутая;
• связная;
• имеет одну особую точку — касп;
• имеет одну ось симметрии.

Базовая окружность есть гиперболизм грушевидной квартики.

Грушевидную квартику изучали английский математик Джон Валлис в 1685 году, французский математик Пьер Бонне в 1844 году и французский математик Гастон Сели-Лонгшан в 1886 году.

Определения грушевидной квартики

Определение и уравнение

Грушеви́дная кварти́ка (англ. piriform quartic; pear-shaped quartic; pear-shaped curve) — антигиперболизм окружности $(x-a)^{2}+y^{2}=a^{2}$ радиуса $a$ с началом координат на окружности и прямой $x=b$, перпендикулярной диаметру окружности с концом в начале координат, определяется следующим уравнением в декартовых координатах:

$x^{4}-2ax^{3}=-b^{2}y^{2}$

или

$y=\pm {\frac {x}{b}}{\sqrt {2ax-x^{2}}}.$

Синонимы:

• капля (англ. drop of water);
• колышек (англ. peg-top).

Грушевидная квартика — это кривая, обладающая следующими простыми свойствами:

• ограниченная и замкнутая;
• связная;
• имеет одну особую точку — касп;
• имеет одну ось симметрии.

Приведённое выше уравнение грушевидной квартики в декартовой системе координат

$x^{4}-2ax^{3}=-b^{2}y^{2}$

(с площадью $S={\frac {\pi a^{3}}{b}}$ области, ограниченной грушевидной квартикой) может быть записано по-другому:

• в виде следующего канонического уравнения эллипса:

${\frac {(x-a)^{2}}{a^{2}}}+{\frac {y^{2}}{x^{2}}}=1$

или

${\frac {(x-b)^{2}}{b^{2}}}+{\frac {y^{2}}{x^{2}}}=1,$

где $a=b$ (и площадью $S=\pi a^{2}$ кривой);

• в сокращённой форме:

$x^{4}-dx^{3}=-b^{2}y^{2},$

где $d=2a$ — диаметр базовой окружности антигиперболизма (и площадь $S={\frac {\pi d}{8b}}$ кривой);

• в очень сокращённой форме:

$x^{4}-x^{3}=-y^{2},$

где $2a=b=1$ (и площадь $S={\frac {\pi }{8}}$ кривой);

• с изменённым параметром $b={\frac {a^{2}}{p}}$ (и площадью $S=\pi ap\;$ кривой, которая совпадает с площадью эллипса с полуосями $a$ и $p$), теперь параметр $a$ масштабирует кривую вдоль оси симметрии:

$p^{2}x^{3}(2a-x)=a^{4}y^{2}.$

Все уравнения, рассмотренные выше, имеют горизонтальную ось симметрии (совпадающую с оью абсцисс) и касп, расположенный слева при $a>0.$ Но касп можно расположить на графике и справа, записав уравнение грушевидной квартики в следующей форме при $a>0\!:$

$x^{4}+2ax^{3}=-b^{2}y^{2}.$

У всех уравнений, рассмотренные выше, ось симметрии совпадает с осью абсцисс. У следующих уравнений ось симметрии грушевидной квартики совпадает с осью ординат:

• касп расположен внизу при $a>0$:

$y^{4}-2ay^{3}=-b^{2}x^{2};$

• касп расположен вверху при $a>0$:

$y^{4}+2ay^{3}=-b^{2}x^{2}.$

Частные случаи

Антиверзиера — частный случай грушевидной квартики при $b=2a$ со следующим уравнением:

$x^{4}-2ax^{3}=-4a^{2}y^{2}.$

При обобщении антиверзиеры до грушевидной квартики её уравнение записывают в следующем виде:

$x^{4}-2ax^{3}=-4{\frac {a^{4}}{b^{2}}}y^{2}.$

Волчок, или юла — частный случай грушевидной квартики при $b=a$ со следующим уравнением:

$x^{4}-2ax^{3}=-a^{2}4y^{2}.$

Жемчужная кривая четвёртого порядка — название двух разных кривых, одна из которых — частный случай грушевидной квартики при $b=2a,$ со следующими уравнениями:

$x^{4}-2ax^{3}=-4a^{2}y^{2},$

$x^{4}-2ax^{3}=-y^{4}.$

Жемчужная кривая четвёртого порядка обычно имеет форму с осью симметрии, параллельной оси ординат:

$y^{4}-2ay^{3}=-4a^{2}x^{2},$

$y^{4}-2ay^{3}=-x^{4}.$

Квартика Бонне — частный случай грушевидной квартики при $b=2a$ со следующим уравнением:

$x^{4}-2ax^{3}=-4a^{2}y^{2}.$

Вывод уравнения и геометрическое построение

Получить грушевидную квартику $F(X,Y)$ путём антигиперболизма $Y={\frac {xy}{b}},$ $X=x$ базовой окружности $(x-a)^{2}+y^{2}=a^{2}$ радиуса $a$ с началом координат на этой окружности и базовой прямой $x=b$, перпендикулярной диаметру окружности с концом в начале координат можно двумя способами:

• исходя из уравнения базовой окружности:

$(x-a)^{2}+y^{2}=a^{2},$

$(x-a)^{2}+\left({\frac {bY}{x}}\right)^{2}=a^{2},$

$X^{4}-2aX^{3}=-b^{2}Y^{2};$

• исходя из преобразования антигиперболизма:

$Y={\frac {xy}{b}},$

$Y^{2}={\frac {x^{2}}{b^{2}}}y^{2},$

$b^{2}Y^{2}=x^{2}(a^{2}-(x-a)^{2}),$

$X^{4}-2aX^{3}=-b^{2}Y^{2}.$

Получаем, что преобразование антигиперболизма окружности:

• сохраняет абсциссу $x;$
• изменяет ординату $y$ пропорционально абсциссе и ординате с постоянным коэффициентом ${\frac {1}{b}}.$

Геометрическое построение красной точки грушевидной квартики

Выясним роль базовых окружности и прямой, построив грушевидную квартику геометрически (см. рисунок справа):

• выберем внутри диаметра базовой окружности произвольную точку с абсциссой $x'$, которая будет также и абсциссой грушевидной квартики;
• проведём прямую $x=x'$, которая пересечётся с базовой окружностью в точке $P''=(x',\,y'),\,$ на которой будет расположена точка грушевидной квартики;
• проведём базовую прямую $x=b$;
• проведём прямую $y=y'$, которая пересечётся с базовой прямой $x=b$ в точке $P'=(b,\,y')$;
• проведём прямую через начало координат и точку $P'$, которая пересечётся с прямой $x=x'$ в точке $P$ — точке грушевидной квартики.

Получим уравнение грушевидной квартики в декартовых координатах, исходя из её геометрического построения:

• пусть уравнение прямой $(P',\,P)$ есть

$y=mx$,

где $m$ — некоторый угловой коэффициент, тогда декартовы координаты точки грушевидной квартики будут

$(x',\,mx')=(x',\,y');$

• координата точки $P'$ будет $(b,\,mb),$ а точки $P''$ — $(x',\,mb);$
• поскольку точка $P''$ лежит на базовой окружности, то

$m^{2}b^{2}=-x'^{2}+2ax'$

$b^{2}y'^{2}=b^{2}m^{2}x'^{2}=-x'^{4}+2ax'^{3},$

а поскольку $x'$ — произвольная точка, окончательно получаем уравнение грушевидной квартики в виде

$X^{4}-2aX^{3}=-b^{2}Y^{2}.$

Из подобных треугольников 0x'P и 0bP' этого геометрического построения также можно получить уравнения преобразования антигиперболизма, которое зависит только от базовой прямой $x=b$ и не зависит от базовой кривой:

${\frac {Y'}{y'}}={\frac {x'}{b}},$ $X'=x',$

$Y={\frac {xy}{b}},$ $X=x.$

Базовая окружность есть гиперболизм грушевидной квартики.

Уравнение в других координатных системах

Для перевода уравнения кривой из декартовой $(x,\,y)$ в полярную систему координат $(r,\,\varphi )$ (и обратно) используют соотношения

$x=r\cos \varphi ,\,$ $y=r\sin \varphi ,\,$ $x^{2}+y^{2}=r^{2},$

поэтому полярное уравнение грушевидной квартики будет следующим:

$x^{4}-2ax^{3}=-b^{2}y^{2},$

$(r\cos \varphi )^{4}-2a(r\cos \varphi )^{3}=-b^{2}(r\sin \varphi )^{2},$

$b^{2}\sin ^{2}\varphi +r^{2}\cos ^{4}\varphi -2ar\cos ^{3}\varphi =0.$

В параметрическом виде уравнение грушевидной квартики на вещественной декартовой плоскости

$x^{4}-2ax^{3}=-b^{2}y^{2}$

может быть таким:

$x=a(1+\sin t),$

$by=a^{2}(1+\sin t)\cos t,$

где $t={\frac {\pi }{2}}-2\varphi ,$

или таким:

$x=2a\cos ^{2}t=a(1+\cos u),$

$by=4a^{2}\cos ^{3}t\sin t={\frac {a^{2}}{2}}(\sin {2u}+2\sin u),$

где $2t=2\varphi =u.$

Виды грушевидных квартик

В этом разделе грушевидные квартики определяются уравнением

$x^{4}-2ax^{3}=-b^{2}y^{2}.$

Пересечение с осями и экстремумы

Отмечены касп, правая вершина и точки максимума и минимума

Произвольная грушевидная квартика пересекается с осями декартовых координат в следующих точках (см. рисунок справа):

• с осью абсцисс $x=0$ в точках $(0,\,0)$ и $(2a,\,0);$
• с осью ординат $y=0$ в точке $(0,\,0);$
• в точке $(0,\,0)$ находится касп грушевидной квартики с касательной $y=0$ — осью абсцисс;
• в точке $(2a,\,0)$ на оси симметрии находится вершина грушевидной квартики;

Декартовы координаты точек произвольной грушевидной квартики ограничены следующими неравенствами (см. рисунок справа):

• $0\leqslant x\leqslant 2a,$ крайняя левая точка $(0,\,0)$ и крайняя правая $(2a,\,0);$
• $-{\frac {a^{2}}{4b}}3{\sqrt {3}}\leqslant y\leqslant {\frac {a^{2}}{4b}}3{\sqrt {3}},$ минимум кривой $\left({\frac {3}{2}}a,\,-{\frac {a^{2}}{4b}}3{\sqrt {3}}\right)$ и максимум $\left({\frac {3}{2}}a,\,{\frac {a^{2}}{4b}}3{\sqrt {3}}\right);$
• экстремальные точки грушевидной квартики лежат на прямой $x={\frac {3}{4}}a,$ их иногда неправильно называют вершинами.

Точки перегиба

Отмечены касп, правая вершина и точки перегиба

Вычислим вторую производную функции, задающей грушевидную квартику:

$y={\frac {x{\sqrt {x}}}{b}}{\sqrt {2a-x}},$

${\frac {dy}{dx}}={\frac {\sqrt {x}}{b}}{\frac {3a-2x}{\sqrt {2a-x}}},$

${\frac {d^{2}y}{d^{2}x}}={\frac {2x^{2}-6ax+3a^{2}}{b{\sqrt {x}}\left({\sqrt {2a-x}}\right)^{3}}}=$

$={\frac {a(3a-2x)-2x(2a-x)}{b{\sqrt {x}}\left({\sqrt {2a-x}}\right)^{3}}}.$

В точке перегиба вторая производная функции меняет знак, то есть необходимое условие точки перегиба — равенство нулю второй производной функции (а заодно и кривизны кривой). Другими словами, точки перегиба суть решение следующей системы уравнений:

$\left\{{\begin{array}{lll}\displaystyle {\frac {d^{2}y}{d^{2}x}}=0,\\0\leqslant x\leqslant 2a.\end{array}}\right.$

Получаем следующие точки перегиба грушевидной квартики (см. рисунок справа):

$\left(a{\frac {3-{\sqrt {3}}}{2}},\,{\frac {a^{2}}{2b}}{\sqrt {6{\sqrt {3}}-9}}\right),$

лежащие на прямой $x=a{\frac {3-{\sqrt {3}}}{2}}.$

Пересечение с базовой окружностью

Отмечены точки пересечения квартик с базовой окружностью

Грушевидная квартика

$x^{4}-2ax^{3}=-b^{2}y^{2};$

всегда пересекается с базовой окружностью

$(x-a)^{2}+y^{2}=a^{2}$

в двух точках:

• на каспе $(0,\,0),$
• в вершине $(2a,\,0),$

и, кроме того, может пересекаться ещё в точках пересечения базовой прямой с базовой окружностью.

В итоге грушевидные квартики по точкам пересечения с базовой окружностью делятся на три вида (см. рисунок справа):

• при $0<b<2a$ имеем четыре точки пересечения: $(0,\,0),$ $(2a,\,0)$ и $(b,\,\pm {\sqrt {2ab-b^{2}}});$
• для пограничной квартики Бонне с $b=2a$ две предыдущие точки пересечения $(b,\,\pm {\sqrt {2ab-b^{2}}})$ сливаются с точкой $(2a,\,0),$ остаются две точки пересечения: $(0,\,0)$ и «тройная» $(2a,\,0);$
• при $b>2a$ имеем две обычные точки пересечения: $(0,\,0)$ и $(2a,\,0).$

Кривизна и вершины

Показаны графики соответствующих функций ориентированной кривизны, отмечены их экстремальные точки и показана кривая, на которой лежат эти точки

Грушевидная квартика

$x^{4}-2ax^{3}=-b^{2}y^{2}$

всегда пересекается со своей осью симметрии

$y=0$

в двух вершинах в силу этой симметрии:

• на каспе $(0,\,0)$ — бывшей вершине,
• в вершине $(2a,\,0),$

и, кроме того, может иметь ещё две вершины в точках, определяемых при помощи кривизны грушевидной квартики

$\kappa (x)={\frac {|y''|}{({\sqrt {1+y'^{2}}})^{3}}},$

а именно: в точках, в которых первая производная её кривизны, или ориентированной кривизны

$\kappa _{o}(x)={\frac {y''}{({\sqrt {1+y'^{2}}})^{3}}},$

равна нулю (см. графики функций кривизны на рисунке справа):

${\frac {d\kappa _{o}(x)}{dx}}={\frac {d}{dx}}{\frac {y''}{({\sqrt {1+y'^{2}}})^{3}}}=$

$={\frac {d}{dx}}{\frac {b^{2}(a(3a-2x)-2x(2a-x))}{{\sqrt {x}}\left({\sqrt {x(3a-2x)^{2}+b^{2}(2a-x)}}\right)^{3}}}=0.$

Введём новые переменные — блоки:

$p(x)=2a-x,\,$ $p'(x)=-1,$

$q(x)=3a-2x,\,$ $q'(x)=-2,$

$r(x)=2x^{2}-6ax+3a^{2},\,$ $r'(x)=-2q(x),$

тогда

$y={\frac {x^{3/2}}{b}}{\sqrt {p}},\,$ $y'={\frac {\sqrt {x}}{b}}{\frac {q}{\sqrt {p}}},\,$ $y''={\frac {1}{b{\sqrt {x}}}}{\frac {r}{p^{3/2}}},$

$y'''={\frac {-3a^{3}}{bx^{3/2}p^{5/2}}},\,$ $1+y'^{2}={\frac {b^{2}p+q^{2}x}{b^{2}p}},$

и блочное уравнение производной ориентированной кривизны будет иметь следующий вид:

$\kappa _{o}'(x)=\left({\frac {y''}{(1+y'^{2})^{3/2}}}\right)'=$

$={\frac {y'''}{(1+y'^{2})^{3/2}}}-{\frac {3y'y''^{2}}{(1+y'^{2})^{5/2}}}=$

$={\frac {-3a^{3}(b^{2}p+q^{2}x)}{b^{3}x^{3/2}p^{7/2}(1+y'^{2})^{5/2}}}-{\frac {3q{\sqrt {x}}r^{2}}{b^{3}p^{7/2}x(1+y'^{2})^{5/2}}}=$

$=-3{\frac {a^{3}(b^{2}p+q^{2}x)+qr^{2}x}{b^{3}x^{3/2}p^{7/2}(1+y'^{2})^{5/2}}}=$

$=-3{\frac {(a^{3}(b^{2}p+q^{2}x)+qr^{2}x)(b^{2}p)^{5/2}}{b^{3}x^{3/2}p^{7/2}(b^{2}p+q^{2}x)^{5/2}}}=$

$=-3{\frac {(a^{3}b^{2}p+a^{3}q^{2}x+qr^{2}x)b^{2}}{px^{3/2}(b^{2}p+q^{2}x)^{5/2}}}.$

После упрощения:

$\kappa _{o}'(x)=-3{\frac {(a^{3}b^{2}+2qx(3a^{3}-xp^{2}))b^{2}}{x^{3/2}(b^{2}p+q^{2}x)^{5/2}}}.$

Дальнейший расчёт производной кривизны

Полученной блочной неупрощённой формулы для кривизны досточно во многих случаях, но продолжим расчёт:

$\kappa _{o}'(x)=-3{\frac {(a^{3}b^{2}p+a^{3}q^{2}x+qr^{2}x)b^{2}}{px^{3/2}(b^{2}p+q^{2}x)^{5/2}}}=$

$=-3{\frac {(a^{3}b^{2}p+qx(a^{3}q+r^{2}))b^{2}}{px^{3/2}(b^{2}p+q^{2}x)^{5/2}}}.$

Найдём

$a^{3}q+r^{2}=$

$=a^{3}(3a-2x)+4x^{4}+36a^{2}x^{2}+9a^{4}-$

${}-24ax^{3}+12a^{2}x^{2}-36a^{3}x=$

$=4x^{4}-24ax^{3}+48a^{2}x^{2}-38a^{3}x+12a^{4}=$

$=x^{2}(2x-4a)^{2}-8ax^{3}+32a^{2}x^{2}-38a^{3}x+12a^{4}=$

$=x^{2}(2x-4a)^{2}-2ax(2x-4a)^{2}-6a^{3}x+12a^{4}=$

$=x^{2}(4a-2x)^{2}-2ax(4a-2x)^{2}+3a^{3}(4a-2x)=$

$=2x^{2}p^{2}-4axp^{2}+6a^{3}p=$

$=2p(x^{2}p-2axp+3a^{3})=$

$=2p(3a^{3}-xp^{2}).$

Тогда

$\kappa _{o}'(x)=-3{\frac {(a^{3}b^{2}+2qx(3a^{3}-xp^{2}))b^{2}}{x^{3/2}(b^{2}p+q^{2}x)^{5/2}}}.$

Раскроем блоки, полностью вернёмся к переменным $x$ и $a$:

$\kappa _{o}'(x)=-3{\frac {(a^{3}b^{2}+2(3a-2x)x(3a^{3}-x(2a-x)^{2}))b^{2}}{x^{3/2}(b^{2}(2a-x)+(3a-2x)^{2}x)^{5/2}}}.$

Найдём

$a^{3}b^{2}+2(3a-2x)x(3a^{3}-x(2a-x)^{2})=$

$=a^{3}b^{2}+2(3ax-2x^{2})(3a^{3}-4a^{2}x-x^{3}+4ax^{2})=$

$=a^{3}b^{2}+18a^{4}x-24a^{3}x^{2}+24a^{2}x^{3}-6ax^{4}-$

${}-12a^{3}x^{2}+16a^{2}x^{3}-16ax^{4}+4x^{5}=$

$=4x^{5}-22ax^{4}+40a^{2}x^{3}-36a^{3}x^{2}+18a^{4}x+a^{3}b^{2},$

$b^{2}(2a-x)+(3a-2x)^{2}x=$

$2ab^{2}-xb^{2}+4x^{3}-12ax^{2}+9a^{2}x=$

$4x^{3}-12ax^{2}+(9a^{2}-b^{2})x+2ab^{2}.$

Тогда

$\kappa _{o}'(x)=-3{\frac {(4x^{5}-22ax^{4}+40a^{2}x^{3}-36a^{3}x^{2}+18a^{4}x+a^{3}b^{2})b^{2}}{x^{3/2}(4x^{3}-12ax^{2}+(9a^{2}-b^{2})x+2ab^{2})^{5/2}}}.$

Вершины грушевидных квартик могут быть в точках, в которых первая производная их ориентированной кривизны равна нулю:

$\kappa _{o}'(x)=0,$

то есть в точках

$a^{3}b^{2}+2qx(3a^{3}-xp^{2})=0.$

Отсюда получаем значения $b_{vertex},$ которые соответствуют вершинам грушевидных квартик:

$b_{vertex}^{2}={\frac {2qx(xp^{2}-3a^{3})}{a^{3}}}=0,$

а также:

• из уравнения функции ориентированной кривизны

$\kappa _{o}(x)={\frac {b^{2}(a(3a-2x)-2x(2a-x))}{{\sqrt {x}}\left({\sqrt {x(3a-2x)^{2}+b^{2}(2a-x)}}\right)^{3}}}=0$

получаем уравнение кривой, на которой лежат точки экстремума функций ориентированной кривизны (см. рисунок справа вверху)

$\kappa _{o}(x)={\frac {b_{vertex}^{2}(a(3a-2x)-2x(2a-x))}{{\sqrt {x}}\left({\sqrt {x(3a-2x)^{2}+b_{vertex}^{2}(2a-x)}}\right)^{3}}}=0,$

Показана кривая, на которой лежат вершины грушевидных квартик, и отмечены эти вершины

Показаны графики соответствующих функций кривизны и их экстремальные точки с кривой, на которой они лежат, а также показаны вершины квартик с.кривой, на которой они лежат

а из уравнения грушевидной квартики

$x^{4}-2ax^{3}=-b^{2}y^{2}$

получаем уравнение кривой. на которой лежат вершины грушевидных квартик (см. рисунок справа)

$x^{4}-2ax^{3}=-b_{vertex}^{2}y^{2}.$

Деление на виды грушевидных квартик по вершинам основано на двух грушевидных квартиках, которые существенно отличаются от остальных:

• грушевидная квартика с $b\approx 3,46a$, у которой вместо трёх вершин справа — одна вершина, три вершины слились в одну (см. рисунки справа и справа вверху);
• грушевидная квартика с $b\approx 2,45a$, у которой экстремальная кривизна минимальна из всех экстремальных кривизн грушевидных квартик (см. рисунок справа).

В итоге грушевидные квартики по вершинам делятся на пять вида (см. рисунок справа):

1) при $0<b\lessapprox 2,45a$ имеем касп и три вершины, а также не минимальную экстремальную кривизну;

2) пограничная квартика с $b\approx 2,45a$ имеет касп и три вершины, а также минимальную экстремальную кривизну;

3) при $2,45a\lessapprox b\lessapprox 3,46a$ имеем то же, что и при 1);

4) пограничная квартика с $b\approx 3,46a$ имеет касп и одну тройную вершину, а также не минимальную экстремальную кривизну;

5) при $3,46a\lessapprox b$ имеем то же, что и при 4).

Обобщения грушевидной квартики

Грушевидная квартика обобщается в двух направлениях произвольными степенями переменных:

• как замкнутая кривая — жемчужная кривая (англ. pearl curve) со следующим уравнением:

$x^{s}(2a-x)^{r}=b^{p}y^{p},$

где $a>0,\,$ $p=2n,\,$ $s=2m-1,\,$ $r=2l-1,\,$ $n,m,l\in \mathbb {N} .$ Грушевидная квартика получается при $p=2,\,$ $s=3,\,$ и $r=1.$

• как каплевидная кривая — оторвавшаяся капля (англ. teardrop curve) со следующим уравнением:

$x^{s}(2a-x)^{r}=b^{2}y^{2}.$ Грушевидная квартика получается при $s=3,\,$ и $r=1.$

• как обобщение двух предыдущих случаев — жемчужины Слюза (англ. pearls of de Sluze) со следующим уравнением:

$x^{s}(2a-x)^{r}=b^{p}y^{p},$

с любыми параметрами. Грушевидная квартика получается при $p=2,\,$ $s=3,\,$ и $r=1.$

• Обобщения грушевидной квартики
• 
  Жемчужные кривые, в том числе грушевидная квартика
• 
  Оторвавшиеся капли, в том числе грушевидная квартика
• 
  Жемчужины Слюза, в том числе грушевидная квартика

Как антигиперболизм окружности грушевидная квартика обобщается произвольным расположением полюса вне окружности. В этом случае возникают две ветви антигиперболизма окружности.

Источники

• Квартика // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 266.
• Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка. М.: Физматлит, 1961. 271 с., ил.
• Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве. Справочник с приложенипем дискеты «Плоские кривые». М.: ФАЗИС, 1997. 334 с., ил. ISBN 5-7036-0027-8.
• Ferréol Robert. Piriform quartic // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 28 февраля 2024 на Wayback Machine
• Ferréol Robert. Tear drop curve // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 16 марта 2024 на Wayback Machine
• Lawrence J. D. A Catalog of Special Plane Curves. New York: Dover Publications, Inc., 1972. 218 p.
• jan wassenaar pearls of de Sluze // mathematical curves Архивная копия от 30 ноября 2022 на Wayback Machine
• jan wassenaar piriform // mathematical curves Архивная копия от 29 ноября 2022 на Wayback Machine
• jan wassenaar teardrop curve // mathematical curves Архивная копия от 19 марта 2024 на Wayback Machine
• Weisstein Eric W. Pear-Shaped Curve // Wolfram MathWorld Архивная копия от 19 декабря 2022 на Wayback Machine
• Weisstein Eric W. Piriform Curve // Wolfram MathWorld Архивная копия от 21 августа 2023 на Wayback Machine
• Weisstein Eric W. Teardrop Curve // Wolfram MathWorld Архивная копия от 12 августа 2023 на Wayback Machine