Квадратная антипризма (Tfg;jgmugx gumnhjn[bg)
| Однородная квадратная антипризма | ||
|---|---|---|
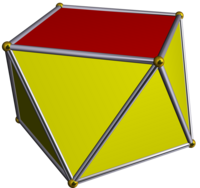 Квадратная антипризма | ||
| Тип |
Призматический однородный многогранник |
|
| Свойства | выпуклый многогранник | |
| Комбинаторика | ||
| Элементы |
|
|
| Грани |
8 треугольников 2 квадрата |
|
| Конфигурация вершины | 3.3.3.4 | |
| Двойственный многогранник | Тетрагональный трапецоэдр[англ.] | |
| Классификация | ||
| Символ Шлефли |
s{2,8} sr{2,4} |
|
| Символ Витхоффа[англ.] | | 2 2 4 | |
| Диаграмма Дынкина |
|
|
| Группа симметрии | D4, [4,2]+, (442), порядок=8 | |
Квадратная антипризма (антикуб[1]) — второй многогранник в бесконечном ряду антипризм, образованных последовательностью треугольных граней, закрытых с обеих сторон многоугольниками. Если все грани являются правильными многоугольниками, антипризма является полуправильным многогранником или однородным многогранником.
Если восемь точек разместить на сфере с целью максимизации расстояний между ними в некотором смысле[уточнить], получившаяся фигура соответствует скорее квадратной антипризме, чем кубу. Специфичные методы распределения точек включают, например, задачу Томпсона (минимизация суммы обратных величин расстояний между точками), максимизацию расстояний от точки до ближайшей или минимизацию суммы всех обратных квадратов расстояний между точками.
Для правильной квадратной антипризмы с длиной ребра объём вычисляется по формуле:
- ,
(также площадь поверхности можно вычислить с учётом того, что развёртка состоит из двух квадратов и восьми равносторонних треугольников).
От каждой вершины квадратной антипризмы можно провести две диагонали, всего у этого многогранника 16 диагоналей. Для полуправильной квадратной антипризмы с ребром эти диагонали будут составлять .
Молекулы с квадратной антипризматической геометрией
[править | править код]
Согласно теории ОЭПВО молекулярной геометрии в химии, которая основывается на принципе максимизации расстояний между точками, квадратная антипризма является наиболее предпочтительной геометрией, если восемь пар электронов окружают центральный атом. Одна из молекул с такой геометрией — ион октафтороксената (VI) (XeF82−) в соли октафтороксената(VI) нитрозила[англ.]. Однако молекула эта далека от идеальной квадратной антипризмы[2]. Очень мало ионов имеют кубическую форму, поскольку такая форма привела бы к сильному отталкиванию лигандов. PaF83− является одним из немногих примеров[3].
Кроме того, сера образует восьмиатомные молекулы S8 как наиболее устойчивую аллотропную форму. Молекула S8 имеет структуру, основанную на квадратной антипризме. В этой молекуле атомы занимают восемь вершин антипризмы, а восемь рёбер между рёбрами соответствуют ковалентной связи между атомами серы.
В архитектуре
[править | править код]
Главное здание в комплексе Центра международной торговли (на месте старого Центра международной торговли, разрушенного 11 сентября 2001) имеет форму очень высокой сужающейся к верху квадратной антипризмы. Здание не является истинной антипризмой, поскольку она сужается к верху — верхний квадрат имеет вдвое меньшую площадь по сравнению с основанием.
Топологически эквивалентные многогранники
[править | править код]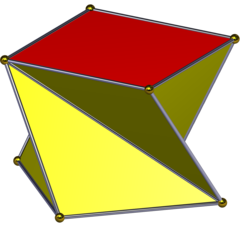
Скрученная призма (по часовой стрелке или против часовой стрелки) может иметь то же расположение вершин. Этот многогранник можно рассматривать как форму, собранную из 4 тетраэдров с вырезанными частями. Однако после вырезания тело нельзя разбить на тетраэдры без добавления новых вершин. Тело имеет половину симметрий однородного тела: Dn, [4,2]+[4][5].
Связанные многогранники
[править | править код]Производные многогранники
[править | править код]Скрученно удлинённая четырёхугольная пирамида является правильногранным многогранником (J10 = М2+А4), полученным удлинением квадратной пирамиды. Подобным же образом, скрученно удлинённая четырёхугольная бипирамида (J17 = М2+А4+М2) является дельтаэдром (многогранником, грани которого являются правильными треугольниками), построенным путём замены обоих квадратов квадратной антипризмы квадратными пирамидами.
Плосконосый двуклиноид (J84 = М25) является другим дельтаэдром, который получается заменой двух квадратов квадратной антипризмы парами равносторонних треугольников. Плосконосую квадратную антипризму (J85 = М28) можно рассматривать как квадратную антипризму, полученную путём вставки цепочки равносторонних треугольников. Клинокорона (J86 = М21) и большая клинокорона (J88 = М23) являются другими правильногранными многогранниками, которые, подобно другим квадратным антипризмам, состоят из двух квадратов и чётного числа равносторонних треугольников.
Квадратная антипризма может быть усечена и альтернирована для образования плосконосых антипризм:
| Антипризма | Усечение t |
Альтернирование[англ.] ht |
|---|---|---|
 s{2,8} |
 ts{2,8} |
 ss{2,8} |
Аналогичные многогранники
[править | править код]Будучи антипризмой, квадратная антипризма принадлежит семейству многогранников, в которые входят октаэдр (который можно рассматривать как треугольную антипризму), пятиугольная антипризма, шестиугольная антипризма и восьмиугольная антипризма[англ.].
| Многогранник | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | ||||||||||||
| Конфигурация | V2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ...∞.3.3.3 |
Квадратная антипризма является первой в ряду плосконосых многогранников и мозаик с вершинной фигурой 3.3.4.3.n.
| 4n2 симметрии плосконосых мозаик: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия 4n2 |
Сферическая | Евклидова | Компактная гиперболическая | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Плосконосые мозаики |

|

|

|

|

|

|

|

|
| Конфиг. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Гиро- мозаики |

|

|

|

|
||||
| Конфиг. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
См. также
[править | править код]Примечания
[править | править код]- ↑ Holleman-Wiberg, 2001, p. 299.
- ↑ Peterson, Holloway, Coyle, Williams, 1971, p. 1238–1239.
- ↑ Norman & Earnshaw, 1997, p. 1275.
- ↑ Gorini, 2003, p. 172.
- ↑ Рисунки скрученных призм и антипризм. Дата обращения: 31 января 2017. Архивировано 12 декабря 2016 года.
Литература
[править | править код]- Inorganic Chemistry / A.F. Holleman, Nils Wiberg, Egon Wiberg. — Academic Press, 2001. — ISBN 0-12-352651-5.
- W. Peterson, A. Holloway, H. Coyle, M. Williams. Antiprismatic Coordination about Xenon: the Structure of Nitrosonium Octafluoroxenate(VI) // Science. — 1971. — Т. 173, вып. 4003. — ISSN 0036-8075. — doi:10.1126/science.173.4003.1238. — . — PMID 17775218.
- Catherine A. Gorini. The Facts on File Geometry Handbook. — New York: Facts On File, Inc, 2003. — ISBN 0-8160-4875-4.
- Norman N. Greenwood, Alan Earnshaw. Chemistry of the Elements (2nd ed.). — Butterworth-Heinemann, 1997. — ISBN 0-08-037941-9.
Ссылки
[править | править код]- Weisstein, Eric W. Antiprism (англ.) на сайте Wolfram MathWorld.
- Square Antiprism Интерактивная модель
- Virtual Reality Polyhedra Архивная копия от 23 февраля 2008 на Wayback Machine www.georgehart.com: The Encyclopedia of Polyhedra
- VRML model
- Conway Notation for Polyhedra Архивная копия от 29 ноября 2014 на Wayback Machine Try: «A4»
Для улучшения этой статьи желательно:
|





