Правильный восьмиугольник (Hjgfnl,udw fkv,bnrikl,unt)

Восьмиугольник
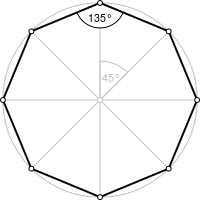Правильный восьмиугольник
Тип	Правильный многоугольник
Рёбра	8
Символ Шлефли	{8}, t{4}
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D8)
Площадь	$2\cot {\frac {\pi }{8}}a^{2}$ $=2(1+{\sqrt {2}})a^{2}\approx 4,828\,a^{2}.$
Внутренний угол	135°
Свойства
выпуклый, вписанный, равносторонний, равноугольный, изотоксальный
Медиафайлы на Викискладе

Правильный восьмиугольник (или октагон от греч. οκτάγωνο) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Правильный восьмиугольник имеет символ Шлефли {8} и может быть построен также как квазиправильный усечённый квадрат, t{4}, в котором перемежаются два типа граней. Усечённый восьмиугольник (t{8}) является шестнадцатиугольником (t{16}).

Свойства

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

• Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его вершинами.
• Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
• Угол правильного восьмиугольника составляет $135^{\circ }$

Формулы расчёта параметров правильного восьмиугольника

Пример:

• t — длина стороны восьмиугольника
• r — радиус вписанной окружности
• R — радиус описанной окружности
• S — площадь восьмиугольника
• k — константа, равная $(1+{\sqrt {2}})\approx 2,414$

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной $kt$, радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

• Радиус вписанной окружности правильного восьмиугольника:

$r={\frac {k}{2}}t$

• Радиус описанной окружности правильного восьмиугольника:

$R=t{\sqrt {\frac {k}{k-1}}}$

• Площадь правильного восьмиугольника:

Через сторону восьмиугольника

$S=2kt^{2}=2(1+{\sqrt {2}})t^{2}\approx 4,828\,t^{2}.$

Через радиус описанной окружности

$S=4\sin {\frac {\pi }{4}}R^{2}=2{\sqrt {2}}R^{2}\approx 2,828\,R^{2}.$

Через апофему (высоту)

$A=8\tan {\frac {\pi }{8}}r^{2}=8({\sqrt {2}}-1)r^{2}\approx 3,314\,r^{2}.$

Площадь через квадрат

Площадь правильного восьмиугольника можно вычислить как площадь усечённого квадрата.

Площадь можно также вычислить как усечение квадрата

$S=A^{2}-a^{2},$

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

$A={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2,414a.$

Тогда площадь равна:

$S=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4,828a^{2}.$

Площадь через A (ширину восьмиугольника)

$S=2({\sqrt {2}}-1)A^{2}\approx 0,828A^{2}.$

Ещё одна простая формула площади:

$\ S=2aA.$

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

$a\approx A/2,414.$

Два катета углового треугольника можно получить по формуле

$e=(A-a)/2.$

Симметрия

11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.

Правильный восьмиугольник имеет группу симметрии Dih₈ порядка 16. Имеется 3 диэдральные подгруппы — Dih₄, Dih₂ и Dih₁, а также 4 циклические подгруппы — Z₈, Z₄, Z₂ и Z₁. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 . Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

Примеры восьмиугольников по их симметриям

r16
d8	g8	p8
d4	g4	p4
d2	g2	p2
a1

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Разрезание правильного восьмиугольника

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта .

Разрезание правильного восьмиугольника

На 6 ромбов

Тессеракт

Применение восьмиугольников

Дорожный знак «Движение без остановки запрещено»

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Другие использования

• 
  Зонты часто имеют восьмиугольную форму
• 
  Знаменитый туркменский ковёр использует восьмиугольный узор
• 
  Триграммы (даосизм) часто представляются восьмиугольниками
• 
  Знаменитая восьмиугольная чашка с острова Белитунг
• 
  Схема лабиринта Реймсского собора

Производные фигуры

• 
  Усечённая квадратная мозаика имеет 2 восьмиугольника около каждой вершины.
  
• 
  Восьмиугольная призма содержит две восьмиугольные грани.
  
• 
  Восьмиугольная антипризма содержит две восьмиугольные грани.
  
• 
  Усечённый кубооктаэдр содержит 6 восьмиугольных граней.
  
• 
  Всеусечённые кубические соты
  

Связанные многогранники

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Усечённые гиперкубы

							...
Восьмиугольник	Усечённый куб	Усечённый тессеракт	Усечённый 5-куб	Усечённый 6-куб	Усечённый 7-куб	Усечённый 8-куб

Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

Расширенные гиперкубы

							...
Октаэдр	Ромбокубооктаэдр	Обструганный тессеракт	Обрубленный 5-куб	Пятиогранённый 6-куб	Шестиогранённый 7-куб	Семиогранённый 8-куб

См. также

• Восьмерик
• Восьмиугольное число
• Октаграмма
• Площадь Октогон в Будапеште, Венгрия
• Сглаженный восьмиугольник

Литература

• У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
• Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google Архивная копия от 2 января 2016 на Wayback Machine  (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275—278. — ISBN 978-1-56881-220-5.