Тело Штейнмеца (Mylk Omywubyeg)
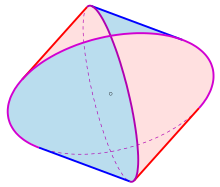
Тело Штейнмеца — это тело, полученное пересечением двух или трёх цилиндров одинакового радиуса, перпендикулярных друг другу. Кривые, образованные пересечением цилиндров, являются эллипсами.
Пересечение двух цилиндров называется бицилиндром. Топологически бицилиндр эквивалентен квадратному осоэдру. Существуют тела, аналогичные по образованию телу Штейнмеца: трицилиндр (пересечение трёх цилиндров) и свод (половина бицилиндра)[1]. Купольный свод[англ.][2] в архитектуре также является сводом.
Тела Штейнмеца названы именем математика Чарлза Протеуса Штейнмеца[3], решившего задачу нахождения объёма пересечения. Однако эта задача была решена задолго до него Архимедом в древней Греции[4][5], Цзу Чунчжи в древнем Китае[6] и Пьеро делла Франческа во времена раннего итальянского Ренессанса[4].

Бицилиндр
[править | править код]
Бицилиндр, образованный двумя цилиндрами с радиусами , имеет объём и площадь поверхности [1][7].
Верхняя половина бицилиндра является квадратным вариантом сомкнутого свода[англ.], куполовидного тела, опирающегося на выпуклый многоугольник, горизонтальные сечения которого являются уменьшенными копиями основания. Имеют место аналогичные формулы вычисления объёма и площади поверхности сомкнутого свода как соответствующих величин (с некоторыми рациональными коэффициентами) призмы с тем же основанием[8].
Получение формулы объёма
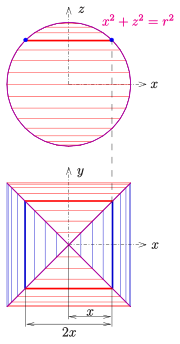
[править | править код]Для получения формулы объёма удобно использовать общую идею вычисления объёма сферы — суммирование тонких цилиндрических слоёв. В нашем случае слоями будут квадратные параллелепипеды (см. рисунок). Тогда получим:
- .
Известно, объёмы вписанного в полусферу конуса (с высотой полусферы и опирающегося на основание полусферы), полусферы и описанного вокруг сферы цилиндра (с высотой полусферы) относятся как 1: 2: 3. Для половины бицилиндра верны аналогичные утверждения:
- Отношения объёмов вписанной квадратной пирамиды (), половины бицилиндра () и описанного прямоугольного параллелепипеда () равны 1: 2: 3.
Аналитический вывод
[править | править код]Рассмотрим формулы цилиндров:
и .
Объём задаётся формулой:
.
С пределами интегрирования:
,
,
.
Подстановкой получим:
.
Доказательство формулы площади
[править | править код]Рассматриваемая поверхность состоит из двух красных и двух синих цилиндрических двуугольников. Один красный двуугольник делится пополам y-z-плоскостью и разворачивается на плоскости так, что половина окружности (пересечение с плоскостью y-z) разворачивается в положительную -ось, а развёрнутый биугол ограничен сверху дугой . Следовательно, площадь этой развёрнутой фигуры (половины двуугольника) равна:

- ,
а площадь полной поверхности равна:
- .
Альтернативное доказательство формулы объёма
[править | править код]Вывод объёма бицилиндра (белого) можно провести путём упаковки в куб (красный). Пересечение плоскости (параллельной осям цилиндра) и бицилиндра образует квадрат, а пересечение с кубом образует больший квадрат. Разница между площадями этих двух квадратов та же, что и у 4 маленьких квадратов (синих). При движении плоскости через тело эти синие квадраты образуют квадратные пирамиды с равнобедренными гранями по углам куба. Пирамиды имеют вершины в серединах четырёх рёбер куба. Продвижение плоскости через весь бицилиндр обрисует 8 пирамид.
-
Метод Цзу Чунчжи (подобен методу неделимых) для вычисления объёма сферы включает вычисление объёма бицилиндра.
-
Связь площади сечения поверхности бицилиндра с сечением куба
Объём куба (красный) минус объём восьми пирамид (синие) равен объёму бицилиндра (белый). Объём 8 пирамид равен , и мы можем теперь вычислить объём бицилиндра .
Трицилиндр
[править | править код]
Пересечение трёх цилиндров с перпендикулярными пересекающимися осями образует поверхность тела с вершинами, в каждой из которых сходятся 3 ребра, и вершинами, в каждой из которых сходятся 4 ребра. Ключевым фактом для определения объёма и площади поверхности является наблюдение, что трицилиндр можно собрать из куба, вершины которого совпадают с вершинами трицилиндра, в которых сходятся 3 ребра (см. рисунок), и 6 криволинейных пирамид (треугольники являются частями поверхностей цилиндров). Объём и площадь поверхности криволинейных треугольников можно вычислить аналогично сделанному выше для бицилиндра[1][7].
Объём трицилиндра равен:
- ,
а площадь поверхности равна:
Пересечение большего числа цилиндров
[править | править код]Для четырёх цилиндров, оси которых соответствуют высотам тетраэдра, объём равен[1][7]:
Для шести цилиндров, оси которых параллельны диагоналям граней куба, объём равен[1][7]:
- .
См. также
[править | править код]Примечания
[править | править код]- ↑ 1 2 3 4 5 Steinmetz Solid (амер. англ.). MathWorld.. Дата обращения: 27 октября 2021. Архивировано 28 октября 2021 года.
- ↑ Купольный свод – это вариант сомкнутого свода. Сомкнутый свод имеет в основании прямоугольник, купольный – квадрат.
- ↑ Eves, 1981, с. 111.
- ↑ 1 2 Peterson, 1997, с. 33–40.
- ↑ Hogendijk, 2002, с. 199–203.
- ↑ Swetz, 1995, с. 142–145.
- ↑ 1 2 3 4 Moore, 1974, с. 181–185.
- ↑ Apostol, Mnatsakanian, 2006, с. 521–540.
Литература
[править | править код]- Howard Eves. Slicing it thin // The mathematical Gardner, Wadsworth International. — 1981. — С. 111.
- Jan Hogendijk. The surface area of the bicylinder and Archimedes' Method // Historia Mathematica. — 2002. — Т. 29, вып. 2. — С. 199–203. — doi:10.1006/hmat.2002.2349.
- Frank J. Swetz. The volume of a sphere: A Chinese derivation // The Mathematics Teacher. — 1995. — Февраль (т. 88, вып. 2). — С. 142–145. — .
- Mark A. Peterson. The geometry of Piero della Francesca // The Mathematical Intelligencer. — 1997. — Т. 19, вып. 3. — С. 33–40. — doi:10.1007/BF03025346.
- Moore, M. Symmetrical intersections of right circular cylinders // The Mathematical Gazette. — 1974. — Т. 58, вып. 405. — С. 181–185. — doi:10.2307/3615957. — .
- Tom M. Apostol, Mamikon A. Mnatsakanian. Solids circumscribing spheres // American Mathematical Monthly. — 2006. — Т. 113, вып. 6. — С. 521–540. — doi:10.2307/27641977. — .
Ссылки
[править | править код]Для улучшения этой статьи желательно:
|


























