Поверхность Шерка (Hkfyj]ukvm, Oyjtg)

Анимация превращения друг в друга первой и второй поверхностей Шерка: они являются членами одного и того же ассоциированного семейства минимальных поверхностей.

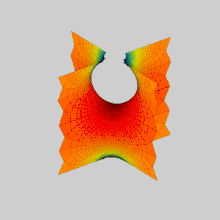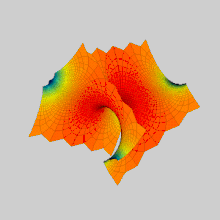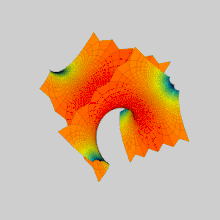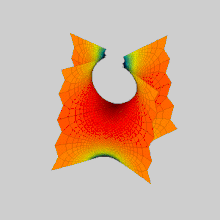
Поверхность Шерка (названа именем Генриха Шерка) является примером минимальной поверхности. Шерк описал две полные вложенные минимальные поверхности в 1834 году. Его первая поверхность является дважды периодической поверхностью, а вторая — просто периодической. Они были третьим нетривиальным примером минимальных поверхностей (первые две — катеноид и геликоид). Две поверхности сопряжены друг другу.

Поверхности Шерка возникают при изучении некоторых задач о минимальных поверхностях и изучении гармонических диффеоморфизмов гиперболического пространства.

Первая поверхность Шерка

Первая поверхность Шерка асимптотически стремится к двум бесконечным семействам параллельных плоскостей, ортогональных друг другу. Поверхности образуют близ z = 0 арки мостов в шахматном порядке. Поверхность содержит бесконечное число прямых вертикальных линий.

Построение простой поверхности Шерка

Поверхность Шерка Σ, заданная как график функции $u(x,y)=\log(\cos(x)/\cos(y))$ для x и y между $-\pi /2$ и $\pi /2$.

Девять периодов поверхности Шерка.

Рассмотрим следующую минимальную поверхность на квадрате на евклидовой плоскости: для натурального числа n найти минимальную поверхность $\Sigma _{n}$ как график некоторой функции

$u_{n}:\left(-{\tfrac {\pi }{2}},+{\tfrac {\pi }{2}}\right)\times \left(-{\tfrac {\pi }{2}},+{\tfrac {\pi }{2}}\right)\to \mathbb {R}$

так что

$\lim _{y\to \pm \pi /2}u_{n}\left(x,y\right)=+n$ для $-{\tfrac {\pi }{2}}<x<+{\tfrac {\pi }{2}},$

$\lim _{x\to \pm \pi /2}u_{n}\left(x,y\right)=-n$ для $-{\tfrac {\pi }{2}}<y<+{\tfrac {\pi }{2}}.$

То есть, u_n удовлетворяет уравнению минимальной поверхности

$\mathrm {div} \left({\tfrac {\nabla u_{n}(x,y)}{\sqrt {1+|\nabla u_{n}(x,y)|^{2}}}}\right)\equiv 0$

и

$\Sigma _{n}=\left\{(x,y,u_{n}(x,y))\in \mathbb {R} ^{3}\left|-{\tfrac {\pi }{2}}<x,y<+{\tfrac {\pi }{2}}\right.\right\}.$

Что будет с поверхностью при стремлении n к бесконечности? Ответ дал Х. Шерк в 1834 году: предельная поверхность $\Sigma$ является графиком функции

$u:\left(-{\tfrac {\pi }{2}},+{\tfrac {\pi }{2}}\right)\times \left(-{\tfrac {\pi }{2}},+{\tfrac {\pi }{2}}\right)\to \mathbb {R} ,$

$u(x,y)=\log \left({\tfrac {\cos(x)}{\cos(y)}}\right).$

То есть поверхность Шерка над квадратом равна

$\Sigma =\left\{\left.\left(x,y,\log \left({\tfrac {\cos(x)}{\cos(y)}}\right)\right)\in \mathbb {R} ^{3}\right|-{\tfrac {\pi }{2}}<x,y<+{\tfrac {\pi }{2}}\right\}.$

Более общие поверхности Шерка

Можно рассмотреть похожие задачи с минимальными поверхностями на других четырёхугольниках на евклидовой плоскости. Можно также рассмотреть ту же задачу на четырёхугольниках на гиперболической плоскости. В 2006 году Гарольд Розенберг и Паскаль Коллин использовали гиперболические поверхности Шерка для построения гармонического диффеоморфизма из комплексной плоскости в гиперболическую плоскость (единичный диск с гиперболической метрикой), опровергая тем самым гипотезу гипотеза Шёна — Яу.

Вторая поверхность Шерка

Вторая поверхность Шерка

Вторая поверхность Шерка глобально выглядит как две ортогональные плоскости, пересечение которых состоит из последовательности туннелей в чередующихся направлениях. Их пересечения с горизонтальными плоскостями состоит из чередующихся гипербол.

Поверхность задаётся уравнением:

$\sin(z)-\mathrm {sh} \,(x)\mathrm {sh} \,(y)=0$

Поверхность имеет Параметризация Вейерштрасса — Эннепера $f(z)={\tfrac {4}{1-z^{4}}}$, $g(z)=iz$ и может быть параметризована как:

$x(r,\theta )=2\Re (\ln(1+re^{i\theta })-\ln(1-re^{i\theta }))=\ln \left({\tfrac {1+r^{2}+2r\cos \theta }{1+r^{2}-2r\cos \theta }}\right)$

$y(r,\theta )=\Re (4i\tan ^{-1}(re^{i\theta }))=\ln \left({\tfrac {1+r^{2}-2r\sin \theta }{1+r^{2}+2r\sin \theta }}\right)$

$z(r,\theta )=\Re (2i(-\ln(1-r^{2}e^{2i\theta })+\ln(1+r^{2}e^{2i\theta }))=2\tan ^{-1}\left({\tfrac {2r^{2}\sin 2\theta }{r^{4}-1}}\right)$

для $\theta \in [0,2\pi )$ и $r\in (0,1)$. Это даёт один период поверхности, который может быть распространён в z-направлении симметрией.

Поверхность обобщил Х. Кархер в семейство сёдл пилона периодических минимальных поверхностей.

В литературе по ошибке эту поверхность называют пятой поверхностью Шерка. Чтобы исключить путаницу, полезно упоминать поверхность как поверхность Шерка одного периода или как башню Шерка.

Ссылки

• Sabitov, I.Kh. (2001), "Scherk_surface", in Hazewinkel, Michiel (ed.), Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
• Scherk's first surface in MSRI Geometry [1]
• Scherk's second surface in MSRI Geometry [2]
• Scherk's minimal surfaces in Mathworld [3] Архивная копия от 21 февраля 2020 на Wayback Machine