Гексамино (Iytvgbnuk)

"Гексамино" — шестиклеточное полимино, то есть плоская фигура, состоящая из шести равных квадратов, соединённых сторонами. С фигурами гексамино, как со всеми полимино, связано много задач занимательной математики.

35 фигур гексамино

Если не считать различными фигуры, совпадающие при поворотах и зеркальных отражениях, то различных («свободных») форм гексамино насчитывается 35 (см. рисунок). Существует 60 видов «односторонних» гексамино (если зеркальные отражения считаются различными фигурами) и 216 видов «фиксированных» гексамино (различными считаются также и повороты).

Классификация гексамино по симметрии

35 свободных фигур гексамино по их свойствам симметрии можно разделить на 5 категорий:

• 20 фигур гексамино (на рисунке изображены серым цветом) асимметричны;
• 6 гексамино (изображены красным) имеют ось симметрии, параллельную линиям квадратной сетки;
• 2 гексамино (изображены зелёным) имеют диагональную ось симметрии;
• 5 гексамино (изображены синим) имеют центральную (вращательную) симметрию второго порядка;
• 2 гексамино (изображены фиолетовым) имеют две оси симметрии, параллельных линиям сетки.

Для односторонних гексамино (то есть если зеркальные отражения фигур считать различными), первая и четвёртая категории удваиваются в численности, что даёт дополнительно 25 гексамино, то есть в общей сложности 60. Для фиксированных гексамино (то есть если повороты также рассматривать как различные фигуры), то первая категория возрастёт в восемь раз по сравнению со свободнми гексамино, следующие три категории — в четыре раза, а из последней категории — в два. Это даст $20\times 8+(6+2+5)\times 4+2\times 2=216$ фиксированных гексамино.

Составление фигур из гексамино

Квадрат 15×15 с отверстием 3×5, составленный из гексамино

Хотя полный набор из 35 гексамино имеет общую площадь 210 квадратов, из них невозможно составить какой-либо прямоугольник с такой площадью (3×70, 5×42, 6×35, 7×30, 10×21, 14×15) — в отличие от 12 пентамино, из которых можно сложить любой из прямоугольников 3×20, 4×15, 5×12 и 6×10. Доказать это можно, раскрасив гексамино и прямоугольник в шахматном порядке. Тогда 11 фигур гексамино будут иметь чётное количество квадратов обоих цветов (2 белых и 4 чёрных или наоборот), а остальные 24 гексамино — нечётное (3 белых и 3 чёрных). Таким образом, в любой фигуре, составленной из полного набора гексамино, число квадратов каждого цвета будет чётным. Но любой прямоугольник из 210 квадратов будет иметь 105 чёрных квадратов и 105 белых, то есть нечётное число.

Тем не менее, есть другие симметричные фигуры из 210 квадратов, которые могут быть составлены из гексамино. Например, квадрат 15×15 с прямоугольным отверстием 3×5 в центре имеет 106 белых и 104 чёрных квадрата (или наоборот) и может быть составлен из полного набора в 35 гексамино.

Некоторые симметричные укладки гексамино

• 
  «Параллелограмм» 15×14 с зубчатыми боковыми сторонами
• 
  Прямоугольник 19×11 с одноклеточным выступом
• 
  Прямоугольник 13×16 с двумя выступами
• 
  «Треугольник» с зубчатой гипотенузой
• 
  Прямоугольник 17×15 с крестообразным отверстием

Кроме того, из 60 односторонних гексамино, имеющих общую площадь в 360 единичных квадратов, можно составить прямоугольники 5×72, 6×60, 8×45, 9×40, 10×36, 12×30, 15×24 и 18×20.

Развёртки куба

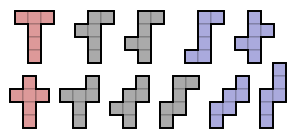
11 из 35 фигур гексамино являются развёртками куба (см. рисунок). Сложить из них прямоугольник площадью в 66 единичных квадратов невозможно.

Литература

• Голомб С.В.. Полимино = Polyominoes / Пер. с англ. В. Фирсова. Предисл. и ред. И. Яглома. — М.: Мир, 1975. — 207 с.
• Solomon W. Golomb. Polyominoes. — 2nd ed. — Princeton, New Jersey: Princeton University Press, 1994. — ISBN 0-691-02444-8.
• Гарднер М. Математические новеллы. — М.: Мир, 1974.
• D. Hugh Redelmeier. Counting polyominoes: yet another attack // Discrete Mathematics : журнал. — 1981. — Vol. 36. — P. 191–203. — doi:10.1016/0012-365X(81)90237-5.
• Daniel A. Rawsthorne. Tiling complexity of small n-ominoes (n<10) // Discrete Mathematics : журнал. — 1988. — Vol. 70. — P. 71–75. — doi:10.1016/0012-365X(88)90081-7.
• Glenn C. Rhoads. Planar tilings by polyominoes, polyhexes, and polyiamonds // Journal of Computational and Applied Mathematics : журнал. — 2005. — Vol. 174. — P. 329–353. — doi:10.1016/j.cam.2004.05.002.