Баллистическая проводимость (>gllnvmncyvtgx hjkfk;nbkvm,)

Баллистическая проводимость (баллистический транспорт) — это направленный поток (или транспорт) носителей заряда (обычно электронов) или частиц, несущих энергию, на относительно большие расстояния в материале без существенного изменения квазиимпульса. В общем, удельное сопротивление материала существует потому, что электрон, двигаясь внутри среды, рассеивается примесями, дефектами, тепловыми колебаниями ионов в кристаллическом твёрдом телё или, вообще, любым свободно движущимся атомом/молекулой, составляющим газ или жидкость. Без рассеяния электроны просто подчиняются второму закону движения Ньютона на нерелятивистских скоростях.

Среднюю длину свободного пробега частицы можно описать как среднюю длину, которую частица может свободно перемещать, то есть до столкновения, которое могло бы изменить её импульс существенно. Длину свободного пробега можно увеличить, уменьшив количество примесей в кристалле или понизив его температуру. Баллистический транспорт наблюдается, когда средняя длина свободного пробега частицы (намного) превышает размеры среды, через которую движется частица. Частица может менять своё движение только при столкновении со стенками.

Баллистическая проводимость обычно наблюдается в квазиодномерных структурах, таких как углеродные нанотрубки или кремниевые нанопроволоки, из-за экстремальных эффектов размерного квантования в этих материалах. Баллистическая проводимость не ограничивается электронами (или дырками), но также может применяться и к другим квазичастицам (например, фононам). В качестве конкретного примера баллистический перенос можно наблюдать в металлической нанопроволоке: из-за небольшого размера проволоки (нанометровый масштаб или масштаб 10⁻⁹ метров) и средней длины свободного пробега, которая может превышать наблюдаемую в металле.

Баллистическая проводимость отличается от сверхпроводимости 1) конечным ненулевым сопротивлением и 2) отсутствием эффекта Мейснера в материале. Наличие сопротивления подразумевает, что тепло рассеивается в контактах за пределами объёма «баллистического» проводника, где могут иметь место эффекты неупругого рассеяния.

Теория

Механизмы рассеяния

В общем, носители заряда демонстрируют баллистическую проводимость, когда $L\leq \lambda _{\rm {MFP}}$, где $L$ — длина активной части устройства (например, канала в MOSFET). $\lambda _{\rm {MFP}}$ — это средняя длина свободного пробега носителя тока, которую можно определить по правилу Маттиссена, записанному здесь для электронов:

${\frac {1}{\lambda _{\mathrm {MFP} }}}={\frac {1}{\lambda _{\mathrm {el-el} }}}+{\frac {1}{\lambda _{\mathrm {ap} }}}+{\frac {1}{\lambda _{\mathrm {op,ems} }}}+{\frac {1}{\lambda _{\mathrm {op,abs} }}}+{\frac {1}{\lambda _{\mathrm {impurity} }}}+{\frac {1}{\lambda _{\mathrm {defect} }}}+{\frac {1}{\lambda _{\mathrm {boundary} }}}$

где

• $\lambda _{\mathrm {el-el} }$ — длина электрон-электронного рассеяния,
• $\lambda _{\mathrm {ap} }$ — длина рассеяния акустических фононов (испускания и поглощения),
• $\lambda _{\mathrm {op,ems} }$ — длина рассеяния излучения оптических фононов,
• $\lambda _{\mathrm {op,abs} }$ — длина рассеяния оптического фонона при поглощении,
• $\lambda _{\mathrm {impurity} }$ — длина рассеяния электронов на примеси,
• $\lambda _{\mathrm {defect} }$ — длина рассеяния электронов на дефектах,
• и $\lambda _{\mathrm {boundary} }$ — длина рассеяния электрона на границе.

В механизмах рассеяния обычно доминирует излучение оптических фононов, что зависит от материала и условий транспорта. Существуют также другие механизмы рассеяния, применимые к различным носителям, которые здесь не рассматриваются (например, рассеяние фононов на удалённой границе раздела, процессы переброса). Чтобы получить эти характерные скорости рассеяния, нужно было бы вывести гамильтониан и провести вычисления используя золотое правило Ферми для рассматриваемой системы.

Полевой транзистор на основе графеновых нанолент (GNR-FET). Здесь контакты A и B находятся при двух разных уровнях Ферми $E_{\rm {F_{A}}}$ и $E_{\rm {F_{B}}}$.

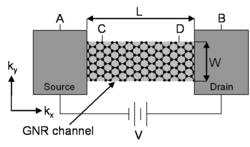
Формализм Ландауэра — Бюттикера

В 1957 году Рольф Ландауэр предположил, что проводимость в одномерной системе можно рассматривать как задачу распространения волны. Для одномерного полевого транзистора с нанолентой графена (GNR-FET) справа (где канал предполагается баллистическим) ток от A до B, определяемый кинетическим уравнением Больцмана, равен

$I_{\rm {AB}}={\frac {g_{\text{s}}e}{h}}\int _{E_{\rm {F_{B}}}}^{E_{\rm {F_{A}}}}M(E)f^{\prime }(E)T(E)dE$ ,

где g_s = 2, из-за спинового вырождения, e — заряд электрона, h — постоянная Планка, $E_{\rm {F_{A}}}$ и $E_{\rm {F_{B}}}$ — уровни Ферми A и B, M(E) — число распространяющихся мод в канале, f ’(E) — отклонение от равновесного распределения электронов (возмущение), а T(E) — вероятность прохождения (Т = 1 для баллистики). По определению кондактанса

$G={\frac {I}{V}}$ ,

Разница между уровнями Ферми в контактах составляет примерно $eV=E_{\rm {F_{A}}}-E_{\rm {F_{B}}}$. Отсюда следует, что

$G=G_{0}MT$, с $G_{0}={\frac {2e^{2}}{h}}$

где M — количество мод в канале, включая спиновое вырождение. Величина $G_{0}$ известна как квант проводимости. Контакты имеют множество режимов из-за их большего размера по сравнению с каналом. И наоборот, квантовое ограничение в канале 1D GNR позволяет существованию только малому количество мод и ограничениями, налагаемыми зонной структурой и зоной Бриллюэна. Например, электроны в углеродных нанотрубках имеют две междолинные моды и две спиновые моды. Так как контакты и канал графеновой наноленты соединены контактами, то вероятность пропускания меньше на контактах А и Б,

$T\approx {\frac {M}{M_{\rm {contact}}}}$ .

Таким образом, квантовая проводимость примерно одинакова, если её измерить в точках A и B или C и D.

Формализм Ландауэра — Бюттикера справедлив до тех пор, пока частицы несущие ток когерентны (что означает, что длина активного канала меньше средней длины фазовой когерентности), а функции передачи можно рассчитать из уравнения Шрёдингера или аппроксимировать с помощью квазиклассического приближения, например приближение ВКБ. Следовательно, даже в случае идеального баллистического транспорта существует фундаментальная баллистическая проводимость, которая насыщает ток устройства с сопротивлением примерно 12,9 кОм на моду (учитывая спиновое вырождение). Однако существует обобщение формализма Ландауэра — Бюттикера, применимое к нестационарным задачам при наличии диссипации энергии.

Важность

Баллистическая проводимость позволяет использовать квантово-механические свойства волновых функций электронов. Баллистический перенос является когерентным с точки зрения волновой механики. Такие явления, как двухщелевая интерференция, пространственный резонанс (и другие оптические или микроволновые эффекты) могут быть использованы в электронных системах на наноуровне, в системах, включая нанопроволоки и нанотрубки.

Широко распространённое явление электрического контактного сопротивления возникает, когда электрический ток, протекающий через шероховатую поверхность раздела, зависит от количества контактов. Размер и распределение этих контактов определяются топологической структурой контактирующих поверхностей, образующих электрический контакт. В частности, для поверхностей с высокой фрактальной размерностью контакты могут быть очень маленькими. В таких случаях, когда радиус контакта меньше длины свободного пробега электронов $\lambda$, в сопротивлении преобладает механизм Шарвина, при котором электроны баллистически проходят через эти микроконтакты с сопротивлением, которое можно описать следующим образом

$R_{\rm {S}}={\frac {\lambda (\rho _{1}+\rho _{2})}{2a}}.$

Этот термин, где $\rho _{1}$ и $\rho _{2}$ соответствуют удельному сопротивлению двух контактирующих поверхностей, известному как сопротивление Шарвина. Электрические контакты, приводящие к баллистической электронной проводимости, известны как контакты Шарвина. Когда радиус контакта больше длины свободного пробега электронов, контактное сопротивление можно рассматривать классически.

Оптические аналогии

Сравнение со светом даёт аналогию между баллистической и небаллистической проводимостью. Баллистические электроны ведут себя как свет в волноводе или высококачественной оптической системе. Небаллистические электроны ведут себя как свет, рассеянный в молоке или отражённый от белой стены или листа бумаги.

Электроны могут рассеиваться в проводнике несколькими способами. Электроны обладают несколькими свойствами: длиной волны (энергией), направлением, фазой и ориентацией спина. Разные материалы имеют разные вероятности рассеяния, что приводит к разной степени некогерентности (стохастичности). Некоторые виды рассеяния могут вызвать только изменение направления движения электронов, другие могут происхожить с потерей энергии.

Рассмотрим когерентный источник электронов, подключенный к проводнику. На ограниченном расстоянии волновая функция электрона останется когерентной. Вы по-прежнему можете детерминированно предсказать его поведение (и теоретически использовать его для вычислений). После некоторого большего расстояния рассеяние приводит к тому, что каждый электрон имеет немного другую фазу и/или направление. Но потерь энергии по-прежнему почти нет. Подобно монохроматическому свету, проходящему через молоко, электроны подвергаются упругим взаимодействиям. Информация о состоянии электронов на входе при этом теряется. Транспорт становится статистическим и стохастическим. С точки зрения сопротивления стохастическое (неориентированное) движение электронов бесполезно, даже если они несут одинаковую энергию — они движутся термически. Если электроны тоже подвергаются неупругим взаимодействиям, они теряют энергию, и в результате возникает второй механизм сопротивления. Электроны, которые подвергаются неупругому взаимодействию, подобны немонохроматическому свету.

Для корректного использования этой аналогии необходимо учитывать несколько фактов:

1. фотоны — бозоны, а электроны — фермионы;
2. между электронами существует кулоновское отталкивание, поэтому эта аналогия хороша только для одноэлектронной проводимости, поскольку электронные процессы сильно нелинейны и зависят от других электронов;
3. более вероятно, что электрон потеряет больше энергии, чем фотон, из-за ненулевой массы покоя электрона;
4. Взаимодействия электронов с окружающей средой, друг другом и другими частицами обычно сильнее, чем взаимодействия с фотонами и между ними.

Примеры

Как уже упоминалось, наноструктуры, такие как углеродные нанотрубки или графеновые наноленты, часто считаются баллистическими, но эти устройства лишь очень близко напоминают баллистическую проводимость. Их баллистичность составляет около 0,9 при комнатной температуре.

Углеродные нанотрубки и графеновая нанолента

Доминирующим механизмом рассеяния при комнатной температуре является механизм испускания электронов оптических фононов. Если электроны не рассеиваются с достаточным количеством фононов (например, если скорость рассеяния низкая), средняя длина свободного пробега имеет тенденцию быть порядка $\lambda _{MFP}\approx 1{\mu }$м. Таким образом, нанотрубка или графеновая нанолента могут быть хорошим баллистическим проводником, если транспортные электроны не рассеиваются со слишком большим количеством фононов и если устройство длиной около 100 нм. Обнаружено, что такой режим транспорта зависит от структуры края наноленты и энергии электронов.

Изотопно-обогащенный алмаз

Изотопически чистый алмаз может иметь значительно более высокую теплопроводность.