Теория Кирхгофа — Лява (Mykjnx Tnj]iksg — Lxfg)

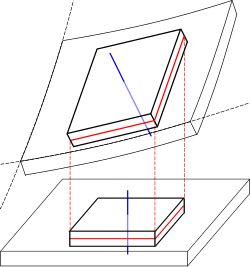
Деформация тонкой пластины с выделенным смещением срединной поверхности (красный) и нормали к срединной поверхности (синий)

Теория Кирхгофа — Лява или теория пластин Кирхгофа — Лява — двумерная математическая модель упругого тела, которая используется для определения напряжений и деформаций в тонких пластинах, подверженных действию сил и моментов при малых изгибах. Эта теория является расширением теории балок Эйлера — Бернулли и была разработана в 1888 году Лявом с использованием постулатов, предложенных Кирхгофом. Теория предполагает, что срединная плоскость может использоваться для представления трёхмерной пластины в двухмерной форме.

В этой теории сделаны следующие кинематические допущения:

• прямые линии, перпендикулярные срединной поверхности, остаются прямыми после деформации;
• прямые линии, перпендикулярные средней поверхности, остаются нормальными к срединной поверхности после деформации;
• и толщина пластины не изменяется при деформации.

Предполагаемые перемещения/смещения

Пусть вектор положения точки недеформированной пластины равен $\mathbf {x}$. Тогда его можно разложить

$\mathbf {x} =x_{1}{\boldsymbol {e}}_{1}+x_{2}{\boldsymbol {e}}_{2}+x_{3}{\boldsymbol {e}}_{3}\equiv x_{i}{\boldsymbol {e}}_{i}\,.$

Векторы ${\boldsymbol {e}}_{i}$ образуют базис декартовой системы координат с началом взятым на срединной поверхности пластины, $x_{1}$ а также $x_{2}$ — декартовы координаты на срединной поверхности недеформированной пластины, а $x_{3}$ — координата направленная вдоль толщины.

Пусть смещение точки на пластине равно $\mathbf {u} (\mathbf {x} )$. Тогда

$\mathbf {u} =u_{1}{\boldsymbol {e}}_{1}+u_{2}{\boldsymbol {e}}_{2}+u_{3}{\boldsymbol {e}}_{3}\equiv u_{i}{\boldsymbol {e}}_{i}$

Это смещение можно разложить на векторную сумму смещения срединной поверхности $u_{\alpha }^{0}$ и смещение вне плоскости $w^{0}$ в направлении $x_{3}$. Мы можем записать смещение срединной поверхности в плоскости как

$\mathbf {u} ^{0}=u_{1}^{0}{\boldsymbol {e}}_{1}+u_{2}^{0}{\boldsymbol {e}}_{2}\equiv u_{\alpha }^{0}{\boldsymbol {e}}_{\alpha }$

Обратите внимание, что индекс $\alpha$ пробегает значения 1 и 2, но не 3.

Тогда из гипотезы Кирхгофа следует, что

${\begin{aligned}u_{\alpha }(\mathbf {x} )&=u_{\alpha }^{0}(x_{1},x_{2})-x_{3}~{\frac {\partial w^{0}}{\partial x_{\alpha }}}\equiv u_{\alpha }^{0}-x_{3}~w_{,\alpha }^{0}~;~~\alpha =1,2\\u_{3}(\mathbf {x} )&=w^{0}(x_{1},x_{2})\end{aligned}}$

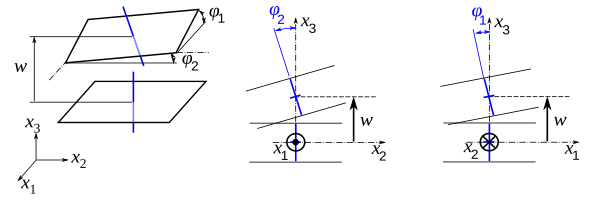
Если $\varphi _{\alpha }$ — углы поворота нормали к срединной поверхности, то в теории Кирхгофа — Лява

$\varphi _{\alpha }=w_{,\alpha }^{0}$

Обратите внимание, что выражение для $u_{\alpha }$ представимо как разложение в ряд Тейлора первого порядка для смещения вокруг срединной поверхности.

Смещение срединной поверхности (слева) и нормали к ней (справа)

Квазистатические пластины Кирхгофа — Лява

Первоначальная теория, разработанная Лавом, применялась для бесконечно малых деформаций и вращений. Фон Карман расширил эту теорию на ситуации, в которых можно было ожидать умеренных вращений.

Соотношения деформация-смещение

Когда деформации в пластине бесконечно малы и повороты нормалей средней поверхности меньше 10° соотношения деформация-смещение (то есть используется разложение до первого порядка малости) принимают вид

${\begin{aligned}\varepsilon _{\alpha \beta }&={\frac {1}{2}}\left({\frac {\partial u_{\alpha }}{\partial x_{\beta }}}+{\frac {\partial u_{\beta }}{\partial x_{\alpha }}}\right)\equiv {\frac {1}{2}}(u_{\alpha ,\beta }+u_{\beta ,\alpha })\\\varepsilon _{\alpha 3}&={\frac {1}{2}}\left({\frac {\partial u_{\alpha }}{\partial x_{3}}}+{\frac {\partial u_{3}}{\partial x_{\alpha }}}\right)\equiv {\frac {1}{2}}(u_{\alpha ,3}+u_{3,\alpha })\\\varepsilon _{33}&={\frac {\partial u_{3}}{\partial x_{3}}}\equiv u_{3,3}\end{aligned}}$

где $\beta =1,2$ как и $\alpha$ .

Используя кинематические предположения, получим

${\begin{aligned}\varepsilon _{\alpha \beta }&={\tfrac {1}{2}}(u_{\alpha ,\beta }^{0}+u_{\beta ,\alpha }^{0})-x_{3}~w_{,\alpha \beta }^{0}\\\varepsilon _{\alpha 3}&=-w_{,\alpha }^{0}+w_{,\alpha }^{0}=0\\\varepsilon _{33}&=0\end{aligned}}$

Следовательно, ненулевые деформации возникают только в плоскостях.

Уравнения равновесия

Уравнения равновесия пластины выводятся из принципа виртуальной работы. Для тонкой пластины при квазистатической поперечной нагрузке $q(x)$ эти уравнения имеют вид

${\begin{aligned}&{\cfrac {\partial N_{11}}{\partial x_{1}}}+{\cfrac {\partial N_{21}}{\partial x_{2}}}=0\\&{\cfrac {\partial N_{12}}{\partial x_{1}}}+{\cfrac {\partial N_{22}}{\partial x_{2}}}=0\\&{\cfrac {\partial ^{2}M_{11}}{\partial x_{1}^{2}}}+2{\cfrac {\partial ^{2}M_{12}}{\partial x_{1}\partial x_{2}}}+{\cfrac {\partial ^{2}M_{22}}{\partial x_{2}^{2}}}=q\end{aligned}}$

где толщина пластины $2h$. В индексной записи

${\begin{aligned}N_{\alpha \beta ,\alpha }&=0\quad \quad N_{\alpha \beta }:=\int _{-h}^{h}\sigma _{\alpha \beta }~dx_{3}\\M_{\alpha \beta ,\alpha \beta }-q&=0\quad \quad M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}\end{aligned}}$

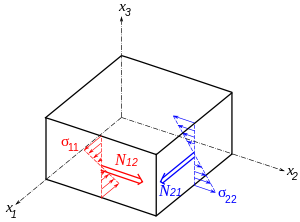
где $\sigma _{\alpha \beta }$ — механические напряжения.

Изгибающие моменты и нормальные напряжения

Моменты и напряжения сдвига

Bending moments and normal stresses

Torques and shear stresses

Вывод уравнения равновесия для малых вращений

Для ситуации, когда напряжения и вращения пластины малы, вариация внутренняя энергия записывается в виде ${\begin{aligned}\delta U&=\int _{\Omega ^{0}}\int _{-h}^{h}{\boldsymbol {\sigma }}:\delta {\boldsymbol {\epsilon }}~dx_{3}~d\Omega =\int _{\Omega ^{0}}\int _{-h}^{h}\sigma _{\alpha \beta }~\delta \varepsilon _{\alpha \beta }~dx_{3}~d\Omega \\&=\int _{\Omega ^{0}}\int _{-h}^{h}\left[{\frac {1}{2}}~\sigma _{\alpha \beta }~(\delta u_{\alpha ,\beta }^{0}+\delta u_{\beta ,\alpha }^{0})-x_{3}~\sigma _{\alpha \beta }~\delta w_{,\alpha \beta }^{0}\right]~dx_{3}~d\Omega \\&=\int _{\Omega ^{0}}\left[{\frac {1}{2}}~N_{\alpha \beta }~(\delta u_{\alpha ,\beta }^{0}+\delta u_{\beta ,\alpha }^{0})-M_{\alpha \beta }~\delta w_{,\alpha \beta }^{0}\right]~d\Omega \end{aligned}}$ где толщина пластины $2h$ и усилия и моменты определяются как $N_{\alpha \beta }:=\int _{-h}^{h}\sigma _{\alpha \beta }~dx_{3}~;~~M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}$ Интегрирование по частям приводит к ${\begin{aligned}\delta U&=\int _{\Omega ^{0}}\left[-{\frac {1}{2}}~(N_{\alpha \beta ,\beta }~\delta u_{\alpha }^{0}+N_{\alpha \beta ,\alpha }~\delta u_{\beta }^{0})+M_{\alpha \beta ,\beta }~\delta w_{,\alpha }^{0}\right]~d\Omega \\&+\int _{\Gamma ^{0}}\left[{\frac {1}{2}}~(n_{\beta }~N_{\alpha \beta }~\delta u_{\alpha }^{0}+n_{\alpha }~N_{\alpha \beta }~\delta u_{\beta }^{0})-n_{\beta }~M_{\alpha \beta }~\delta w_{,\alpha }^{0}\right]~d\Gamma \end{aligned}}$ Симметрия тентора напряжений подразумевает, что $N_{\alpha \beta }=N_{\beta \alpha }$. Отсюда $\delta U=\int _{\Omega ^{0}}\left[-N_{\alpha \beta ,\alpha }~\delta u_{\beta }^{0}+M_{\alpha \beta ,\beta }~\delta w_{,\alpha }^{0}\right]~d\Omega +\int _{\Gamma ^{0}}\left[n_{\alpha }~N_{\alpha \beta }~\delta u_{\beta }^{0}-n_{\beta }~M_{\alpha \beta }~\delta w_{,\alpha }^{0}\right]~d\Gamma$ Проинтегрируем по частям ещё раз $\delta U=\int _{\Omega ^{0}}\left[-N_{\alpha \beta ,\alpha }~\delta u_{\beta }^{0}-M_{\alpha \beta ,\beta \alpha }~\delta w^{0}\right]~d\Omega +\int _{\Gamma ^{0}}\left[n_{\alpha }~N_{\alpha \beta }~\delta u_{\beta }^{0}+n_{\alpha }~M_{\alpha \beta ,\beta }~\delta w^{0}-n_{\beta }~M_{\alpha \beta }~\delta w_{,\alpha }^{0}\right]~d\Gamma$ В случае, отсутствия внешних сил, принцип виртуальной работы подразумевает, что вариация $\delta U=0$. Уравнения равновесия для пластины задаются ${\begin{aligned}N_{\alpha \beta ,\alpha }&=0\\M_{\alpha \beta ,\alpha \beta }&=0\end{aligned}}$ Если пластина испытывает внешнюю распределенную нагрузку $q(x)$, которая направлена по нормали к срединной плоскости и напрвлена вдоль направления $x_{3}$, то внешняя виртуальная работа из-за нагрузки $\delta V_{\mathrm {ext} }=\int _{\Omega ^{0}}q~\delta w^{0}~d\Omega$ Принцип виртуальной работы приводит к уравнениям равновесия ${\begin{aligned}N_{\alpha \beta ,\alpha }&=0\\M_{\alpha \beta ,\alpha \beta }-q&=0\end{aligned}}$

Граничные условия

Граничные условия, необходимые для решения уравнений равновесия в теории пластин, можно получить из граничных условий используемых в принципе виртуальной работы. В отсутствие внешних сил на границе граничные условия имеют вид

${\begin{aligned}n_{\alpha }~N_{\alpha \beta }&\quad \mathrm {or} \quad u_{\beta }^{0}\\n_{\alpha }~M_{\alpha \beta ,\beta }&\quad \mathrm {or} \quad w^{0}\\n_{\beta }~M_{\alpha \beta }&\quad \mathrm {or} \quad w_{,\alpha }^{0}\end{aligned}}$

Обратите внимание, что $n_{\alpha }~M_{\alpha \beta ,\beta }$ — это эффективная сила сдвига.

Материальные соотношения

Соотношения между напряжениями и деформациями для линейной упругой среды имеют вид

${\begin{aligned}\sigma _{\alpha \beta }&=C_{\alpha \beta \gamma \theta }~\varepsilon _{\gamma \theta }\\\sigma _{\alpha 3}&=C_{\alpha 3\gamma \theta }~\varepsilon _{\gamma \theta }\\\sigma _{33}&=C_{33\gamma \theta }~\varepsilon _{\gamma \theta }\end{aligned}}$

поскольку $\sigma _{\alpha 3}$, а также $\sigma _{33}$ не фигурируют в уравнениях равновесия, то неявно предполагается, что эти величины не влияют на баланс импульса и ими можно пренебречь. Остальные соотношения напряжение-деформация в матричной имеют вид

${\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}$

Тогда

${\begin{bmatrix}N_{11}\\N_{22}\\N_{12}\end{bmatrix}}=\int _{-h}^{h}{\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}dx_{3}=\left\{\int _{-h}^{h}{\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}u_{1,1}^{0}\\u_{2,2}^{0}\\{\frac {1}{2}}~(u_{1,2}^{0}+u_{2,1}^{0})\end{bmatrix}}$

и

${\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=\int _{-h}^{h}x_{3}~{\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}dx_{3}=-\left\{\int _{-h}^{h}x_{3}^{2}~{\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}w_{,11}^{0}\\w_{,22}^{0}\\w_{,12}^{0}\end{bmatrix}}$

Жесткости — это величины

$A_{\alpha \beta }:=\int _{-h}^{h}C_{\alpha \beta }~dx_{3}$

Изгибные жесткости (также называемая жесткостью на изгиб) — это величины

$D_{\alpha \beta }:=\int _{-h}^{h}x_{3}^{2}~C_{\alpha \beta }~dx_{3}$

Основные предположения Кирхгофа — Лява приводят к нулевым поперечным силам. Тогда для определения поперечных сил в тонких пластинах Кирхгофа — Лява должны использоваться уравнения равновесия пластины. Для изотропных пластин эти уравнения приводят к выражению

$Q_{\alpha }=-D{\frac {\partial }{\partial x_{\alpha }}}(\nabla ^{2}w^{0})\,.$

В качестве альтернативы эти поперечные силы можно записать как

$Q_{\alpha }={\mathcal {M}}_{,\alpha }$

где

${\mathcal {M}}:=-D\nabla ^{2}w^{0}\,.$

Малые деформации и умеренные вращения

Если повороты нормалей к срединной поверхности находятся в диапазоне от 10$^{\circ }$ до 15$^{\circ }$, то зависимости деформации от смещения можно аппроксимировать как

${\begin{aligned}\varepsilon _{\alpha \beta }&={\tfrac {1}{2}}(u_{\alpha ,\beta }+u_{\beta ,\alpha }+u_{3,\alpha }~u_{3,\beta })\\\varepsilon _{\alpha 3}&={\tfrac {1}{2}}(u_{\alpha ,3}+u_{3,\alpha })\\\varepsilon _{33}&=u_{3,3}\end{aligned}}$

Тогда кинематические допущения теории Кирхгофа — Лява приводят к классической теории пластин с деформациями фон Кармана.

${\begin{aligned}\varepsilon _{\alpha \beta }&={\frac {1}{2}}(u_{\alpha ,\beta }^{0}+u_{\beta ,\alpha }^{0}+w_{,\alpha }^{0}~w_{,\beta }^{0})-x_{3}~w_{,\alpha \beta }^{0}\\\varepsilon _{\alpha 3}&=-w_{,\alpha }^{0}+w_{,\alpha }^{0}=0\\\varepsilon _{33}&=0\end{aligned}}$

Эта теория нелинейна из-за квадратичных членов в соотношениях деформация-перемещение.

Если соотношения деформация-перемещение принимают форму фон Кармана, то уравнения равновесия перепишутся в виде

${\begin{aligned}N_{\alpha \beta ,\alpha }&=0\\M_{\alpha \beta ,\alpha \beta }+[N_{\alpha \beta }~w_{,\beta }^{0}]_{,\alpha }-q&=0\end{aligned}}$

Изотропные квазистатические пластинки Кирхгофа — Лява

В матричной форме, для изотропной и однородной пластины зависимости напряжения от деформации имеют вид

${\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}\,.$

где $\nu$ — коэффициент Пуассона и $E$ модуль Юнга . Моменты, соответствующие этим напряжениям примут вид

${\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&{1-\nu }\end{bmatrix}}{\begin{bmatrix}w_{,11}^{0}\\w_{,22}^{0}\\w_{,12}^{0}\end{bmatrix}}$

или в развернутом виде

${\begin{aligned}M_{11}&=-D\left({\frac {\partial ^{2}w^{0}}{\partial x_{1}^{2}}}+\nu {\frac {\partial ^{2}w^{0}}{\partial x_{2}^{2}}}\right)\\M_{22}&=-D\left({\frac {\partial ^{2}w^{0}}{\partial x_{2}^{2}}}+\nu {\frac {\partial ^{2}w^{0}}{\partial x_{1}^{2}}}\right)\\M_{12}&=-D(1-\nu ){\frac {\partial ^{2}w^{0}}{\partial x_{1}\partial x_{2}}}\end{aligned}}$

где $D=2h^{3}E/[3(1-\nu ^{2})]=H^{3}E/[12(1-\nu ^{2})]$ для пластин толщиной $H=2h$. Используя соотношения напряжения-деформации для пластин, можно показать, что напряжения и моменты связаны соотношениями

$\sigma _{11}={\frac {3x_{3}}{2h^{3}}}\,M_{11}={\frac {12x_{3}}{H^{3}}}\,M_{11}\quad {\text{and}}\quad \sigma _{22}={\frac {3x_{3}}{2h^{3}}}\,M_{22}={\frac {12x_{3}}{H^{3}}}\,M_{22}\,.$

В верхней поверхности пластины, где $x_{3}=h=H/2$, напряжения

$\sigma _{11}={\frac {3}{2h^{2}}}\,M_{11}={\frac {6}{H^{2}}}\,M_{11}\quad {\text{and}}\quad \sigma _{22}={\frac {3}{2h^{2}}}\,M_{22}={\frac {6}{H^{2}}}\,M_{22}\,.$

Чистый изгиб

Для изотропной и однородной пластины при чистом изгибе основные уравнения сводятся к (нет внешних сил)

${\frac {\partial ^{4}w^{0}}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}w^{0}}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}w^{0}}{\partial x_{2}^{4}}}=0\,.$

Здесь мы предположили, что смещения в плоскости не зависят от $x_{1}$ и $x_{2}$. В индексной записи

$w_{,1111}^{0}+2~w_{,1212}^{0}+w_{,2222}^{0}=0$

и в прямой записи

$\nabla ^{2}\nabla ^{2}w=0$

которое известно как бигармоническое уравнение. Изгибающие моменты определяются выражением

${\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}w_{,11}^{0}\\w_{,22}^{0}\\w_{,12}^{0}\end{bmatrix}}$

Вывод уравнений равновесия для чистого изгиба

Для изотропных, однородных пластин под действием чистого изгиба основные уравнения ${\begin{aligned}N_{\alpha \beta ,\alpha }&=0\implies N_{11,1}+N_{21,2}=0~,~~N_{12,1}+N_{22,2}=0\\M_{\alpha \beta ,\alpha \beta }&=0\implies M_{11,11}+2M_{12,12}+M_{22,22}=0\end{aligned}}$ и соотношения напряжения-деформации ${\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}$ Тогда ${\begin{bmatrix}N_{11}\\N_{22}\\N_{12}\end{bmatrix}}={\cfrac {2hE}{(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}u_{1,1}^{0}\\u_{2,2}^{0}\\{\frac {1}{2}}~(u_{1,2}^{0}+u_{2,1}^{0})\end{bmatrix}}$ и ${\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}w_{,11}^{0}\\w_{,22}^{0}\\w_{,12}^{0}\end{bmatrix}}$ Дифференцирование приводит к ${\begin{aligned}N_{11,1}&={\cfrac {2hE}{(1-\nu ^{2})}}\left(u_{1,11}^{0}+\nu ~u_{2,21}^{0}\right)~;~~N_{22,2}={\cfrac {2hE}{(1-\nu ^{2})}}\left(\nu ~u_{1,12}^{0}+u_{2,22}^{0}\right)\\N_{12,1}&={\cfrac {hE(1-\nu )}{(1-\nu ^{2})}}\left(u_{1,21}^{0}+u_{2,11}^{0}\right)~;~~N_{12,2}={\cfrac {hE(1-\nu )}{(1-\nu ^{2})}}\left(u_{1,22}^{0}+u_{2,12}^{0}\right)\end{aligned}}$ и ${\begin{aligned}M_{11,11}&=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\left(w_{,1111}^{0}+\nu ~w_{,2211}^{0}\right)\\M_{22,22}&=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\left(\nu ~w_{,1122}^{0}+w_{,2222}^{0}\right)\\M_{12,12}&=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}(1-\nu )~w_{,1212}^{0}\end{aligned}}$ Подставим результат в основные уравнение, получим ${\begin{aligned}&u_{1,11}^{0}+\nu ~u_{2,21}^{0}+{\tfrac {1}{2}}(1-\nu )\left(u_{1,22}^{0}+u_{2,12}^{0}\right)=0\\&\nu ~u_{1,12}^{0}+u_{2,22}^{0}+{\tfrac {1}{2}}(1-\nu )\left(u_{1,21}^{0}+u_{2,11}^{0}\right)=0\\&w_{,1111}^{0}+\nu ~w_{,2211}^{0}+2(1-\nu )~w_{,1212}^{0}+\nu ~w_{,1122}^{0}+w_{,2222}^{0}=0\end{aligned}}$ Поскольку порядок дифференциации не имеет значения, то $u_{1,12}^{0}=u_{1,21}^{0}$, $u_{2,21}^{0}=u_{2,12}^{0}$, и$w_{,2211}^{0}=w_{,1212}^{0}=w_{,1122}^{0}$. Отсюда ${\begin{aligned}&u_{1,11}^{0}+{\tfrac {1}{2}}(1-\nu )~u_{1,22}^{0}+{\tfrac {1}{2}}(1+\nu )~u_{2,12}^{0}=0\\&u_{2,22}^{0}+{\tfrac {1}{2}}(1-\nu )~u_{2,11}^{0}+{\tfrac {1}{2}}(1+\nu )~u_{1,12}^{0}=0\\&w_{,1111}^{0}+2~w_{,1212}^{0}+w_{,2222}^{0}=0\end{aligned}}$ В прямой тензорной нотации, основное уравнение для пластины $\nabla ^{2}\nabla ^{2}w=0$ где мы предположили, что перемещения $u_{1}^{0},u_{2}^{0}$ постоянны.

Изгиб под действием поперечной нагрузки

Если распределенная поперечная нагрузка $-q(x)$ применяется к пластине, то определяющее уравнение $M_{\alpha \beta ,\alpha \beta }=-q$ . Следуя процедуре, из предыдущего раздела, получаем

$\nabla ^{2}\nabla ^{2}w={\cfrac {q}{D}}~;~~D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}$

В прямоугольных декартовых координатах основное уравнение примет вид

$w_{,1111}^{0}+2\,w_{,1212}^{0}+w_{,2222}^{0}=-{\cfrac {q}{D}}$

а в цилиндрических координатах принимает вид (для круглой пластинки с аксиально-симметричной нагрузкой)

${\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,.$

Решения этого уравнения для различных геометрий и граничных условий можно найти в статье об изгибе пластин.

Вывод уравнений равновесия для поперечной нагрузки

Для поперечно нагруженной пластины без аксиальных деформаций, основное уравнение примет вид $M_{\alpha \beta ,\alpha \beta }=q\implies M_{11,11}+2M_{12,12}+M_{22,22}=q$ где $q$ распределенная поперечная нагрузка (на единицу площади). Замена выражений на производные $M_{\alpha \beta }$ в основном уравнении приводит к $-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\left[w_{,1111}^{0}+2\,w_{,1212}^{0}+w_{,2222}^{0}\right]=q\,.$ Используя для изгибной жёсткости выражение $D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}$ запишем основное уравнение в виде $\nabla ^{2}\nabla ^{2}w=-{\frac {q}{D}}\,.$ В цилиндрических координатах $(r,\theta ,z)$, $\nabla ^{2}w\equiv {\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial w}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}w}{\partial \theta ^{2}}}+{\frac {\partial ^{2}w}{\partial z^{2}}}\,.$ Для аксиально-симметричной нагрузки и круглых пластин, $w=w(r)$, тогда $\nabla ^{2}w\equiv {\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\,.$

Цилиндрический изгиб

При определённых условиях нагружения плоская пластина может изгибаться, принимая форму поверхности цилиндра. Этот тип изгиба называется цилиндрическим изгибом и представляет собой особую ситуацию, когда $u_{1}=u_{1}(x_{1}),u_{2}=0,w=w(x_{1})$. В таком случае

${\begin{bmatrix}N_{11}\\N_{22}\\N_{12}\end{bmatrix}}={\cfrac {2hE}{(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}u_{1,1}^{0}\\0\\0\end{bmatrix}}$

а также

${\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}w_{,11}^{0}\\0\\0\end{bmatrix}}$

и определяющие уравнения становятся к

${\begin{aligned}N_{11}&=A~{\cfrac {\mathrm {d} u}{\mathrm {d} x_{1}}}\quad \implies \quad {\cfrac {\mathrm {d} ^{2}u}{\mathrm {d} x_{1}^{2}}}=0\\M_{11}&=-D~{\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x_{1}^{2}}}\quad \implies \quad {\cfrac {\mathrm {d} ^{4}w}{\mathrm {d} x_{1}^{4}}}={\cfrac {q}{D}}\\\end{aligned}}$

Динамика пластин Кирхгофа — Лява

Динамическая теория тонких пластин ставит задачу о распространении упругих волн в пластинах, а также изучает стоячие волны и режимы колебаний.

Основные уравнения

Основные уравнения динамики пластины Кирхгофа — Лява:

${\begin{aligned}N_{\alpha \beta ,\beta }&=J_{1}~{\ddot {u}}_{\alpha }^{0}\\M_{\alpha \beta ,\alpha \beta }+q(x,t)&=J_{1}~{\ddot {w}}^{0}-J_{3}~{\ddot {w}}_{,\alpha \alpha }^{0}\end{aligned}}$

где для пластины с плотностью $\rho =\rho (x)$ ,

$J_{1}:=\int _{-h}^{h}\rho ~dx_{3}=2~\rho ~h~;~~J_{3}:=\int _{-h}^{h}x_{3}^{2}~\rho ~dx_{3}={\frac {2}{3}}~\rho ~h^{3}$

а также

${\dot {u}}_{i}={\frac {\partial u_{i}}{\partial t}}~;~~{\ddot {u}}_{i}={\frac {\partial ^{2}u_{i}}{\partial t^{2}}}~;~~u_{i,\alpha }={\frac {\partial u_{i}}{\partial x_{\alpha }}}~;~~u_{i,\alpha \beta }={\frac {\partial ^{2}u_{i}}{\partial x_{\alpha }\partial x_{\beta }}}$

Вывод уравнений, регулирующих динамику пластин Кирхгофа — Лява

Полная кинетическая энергия пластины $K=\int _{0}^{T}\int _{\Omega ^{0}}\int _{-h}^{h}{\cfrac {\rho }{2}}\left[\left({\frac {\partial u_{1}}{\partial t}}\right)^{2}+\left({\frac {\partial u_{2}}{\partial t}}\right)^{2}+\left({\frac {\partial u_{3}}{\partial t}}\right)^{2}\right]~\mathrm {d} x_{3}~\mathrm {d} A~\mathrm {d} t$ Таким образом, вариация кинетической энергии $\delta K=\int _{0}^{T}\int _{\Omega ^{0}}\int _{-h}^{h}{\cfrac {\rho }{2}}\left[2\left({\frac {\partial u_{1}}{\partial t}}\right)\left({\frac {\partial \delta u_{1}}{\partial t}}\right)+2\left({\frac {\partial u_{2}}{\partial t}}\right)\left({\frac {\partial \delta u_{2}}{\partial t}}\right)+2\left({\frac {\partial u_{3}}{\partial t}}\right)\left({\frac {\partial \delta u_{3}}{\partial t}}\right)\right]~\mathrm {d} x_{3}~\mathrm {d} A~\mathrm {d} t$ Тут мы используем следующую нотацию ${\dot {u}}_{i}={\frac {\partial u_{i}}{\partial t}}~;~~{\ddot {u}}_{i}={\frac {\partial ^{2}u_{i}}{\partial t^{2}}}~;~~u_{i,\alpha }={\frac {\partial u_{i}}{\partial x_{\alpha }}}~;~~u_{i,\alpha \beta }={\frac {\partial ^{2}u_{i}}{\partial x_{\alpha }\partial x_{\beta }}}$ Тогда $\delta K=\int _{0}^{T}\int _{\Omega ^{0}}\int _{-h}^{h}\rho \left({\dot {u}}_{\alpha }~\delta {\dot {u}}_{\alpha }+{\dot {u}}_{3}~\delta {\dot {u}}_{3}\right)~\mathrm {d} x_{3}~\mathrm {d} A~\mathrm {d} t$ Для пластин Кирхгофа — Лява $u_{\alpha }=u_{\alpha }^{0}-x_{3}~w_{,\alpha }^{0}~;~~u_{3}=w^{0}$ Отсюда ${\begin{aligned}\delta K&=\int _{0}^{T}\int _{\Omega ^{0}}\int _{-h}^{h}\rho \left[\left({\dot {u}}_{\alpha }^{0}-x_{3}~{\dot {w}}_{,\alpha }^{0}\right)~\left(\delta {\dot {u}}_{\alpha }^{0}-x_{3}~\delta {\dot {w}}_{,\alpha }^{0}\right)+{\dot {w}}^{0}~\delta {\dot {w}}^{0}\right]~\mathrm {d} x_{3}~\mathrm {d} A~\mathrm {d} t\\&=\int _{0}^{T}\int _{\Omega ^{0}}\int _{-h}^{h}\rho \left({\dot {u}}_{\alpha }^{0}~\delta {\dot {u}}_{\alpha }^{0}-x_{3}~{\dot {w}}_{,\alpha }^{0}~\delta {\dot {u}}_{\alpha }^{0}-x_{3}~{\dot {u}}_{\alpha }^{0}~\delta {\dot {w}}_{,\alpha }^{0}+x_{3}^{2}~{\dot {w}}_{,\alpha }^{0}~\delta {\dot {w}}_{,\alpha }^{0}+{\dot {w}}^{0}~\delta {\dot {w}}^{0}\right)~\mathrm {d} x_{3}~\mathrm {d} A~\mathrm {d} t\end{aligned}}$ Определим для постоянной по толщине $\rho$ $J_{1}:=\int _{-h}^{h}\rho ~dx_{3}=2~\rho ~h~;~~J_{2}:=\int _{-h}^{h}x_{3}~\rho ~dx_{3}=0~;~~J_{3}:=\int _{-h}^{h}x_{3}^{2}~\rho ~dx_{3}={\frac {2}{3}}~\rho ~h^{3}$ Тогда $\delta K=\int _{0}^{T}\int _{\Omega ^{0}}\left[J_{1}\left({\dot {u}}_{\alpha }^{0}~\delta {\dot {u}}_{\alpha }^{0}+{\dot {w}}^{0}~\delta {\dot {w}}^{0}\right)+J_{3}~{\dot {w}}_{,\alpha }^{0}~\delta {\dot {w}}_{,\alpha }^{0}\right]~\mathrm {d} A~\mathrm {d} t$ Интегрирование по частям даёт $\delta K=\int _{\Omega ^{0}}\left[\int _{0}^{T}\left\{-J_{1}\left({\ddot {u}}_{\alpha }^{0}~\delta u_{\alpha }^{0}+{\ddot {w}}^{0}~\delta w^{0}\right)-J_{3}~{\ddot {w}}_{,\alpha }^{0}~\delta w_{,\alpha }^{0}\right\}~\mathrm {d} t+\left|J_{1}\left({\dot {u}}_{\alpha }^{0}~\delta u_{\alpha }^{0}+{\dot {w}}^{0}~\delta w^{0}\right)+J_{3}~{\dot {w}}_{,\alpha }^{0}~\delta w_{,\alpha }^{0}\right|_{0}^{T}\right]~\mathrm {d} A$ Вариации $\delta u_{\alpha }^{0}$ и $\delta w^{0}$ равны нулю при $t=0$ и $t=T$. Таким образом, после перемены последовательности интегрирования $\delta K=-\int _{0}^{T}\left\{\int _{\Omega ^{0}}\left[J_{1}\left({\ddot {u}}_{\alpha }^{0}~\delta u_{\alpha }^{0}+{\ddot {w}}^{0}~\delta w^{0}\right)+J_{3}~{\ddot {w}}_{,\alpha }^{0}~\delta w_{,\alpha }^{0}\right]~\mathrm {d} A\right\}~\mathrm {d} t+\left|\int _{\Omega ^{0}}J_{3}~{\dot {w}}_{,\alpha }^{0}~\delta w_{,\alpha }^{0}\mathrm {d} A\right|_{0}^{T}$ Интеграция по частям в срединной поверхности даёт ${\begin{aligned}\delta K&=-\int _{0}^{T}\left\{\int _{\Omega ^{0}}\left[J_{1}\left({\ddot {u}}_{\alpha }^{0}~\delta u_{\alpha }^{0}+{\ddot {w}}^{0}~\delta w^{0}\right)-J_{3}~{\ddot {w}}_{,\alpha \alpha }^{0}~\delta w^{0}\right]~\mathrm {d} A+\int _{\Gamma ^{0}}J_{3}~n_{\alpha }~{\ddot {w}}_{,\alpha }^{0}~\delta w^{0}~\mathrm {d} s\right\}~\mathrm {d} t\\&\qquad -\left|\int _{\Omega ^{0}}J_{3}~{\dot {w}}_{,\alpha \alpha }^{0}~\delta w^{0}~\mathrm {d} A-\int _{\Gamma ^{0}}J_{3}~{\dot {w}}_{,\alpha }^{0}~\delta w^{0}~\mathrm {d} s\right|_{0}^{T}\end{aligned}}$ Опять же, поскольку вариации остаются нулевыми в начале и в конце промежутка времени, то $\delta K=-\int _{0}^{T}\left\{\int _{\Omega ^{0}}\left[J_{1}\left({\ddot {u}}_{\alpha }^{0}~\delta u_{\alpha }^{0}+{\ddot {w}}^{0}~\delta w^{0}\right)-J_{3}~{\ddot {w}}_{,\alpha \alpha }^{0}~\delta w^{0}\right]~\mathrm {d} A+\int _{\Gamma ^{0}}J_{3}~n_{\alpha }~{\ddot {w}}_{,\alpha }^{0}~\delta w^{0}~\mathrm {d} s\right\}~\mathrm {d} t$ Для динамического случая вариация внутренней энергии $\delta U=-\int _{0}^{T}\left\{\int _{\Omega ^{0}}\left[N_{\alpha \beta ,\alpha }~\delta u_{\beta }^{0}+M_{\alpha \beta ,\beta \alpha }~\delta w^{0}\right]~\mathrm {d} A-\int _{\Gamma ^{0}}\left[n_{\alpha }~N_{\alpha \beta }~\delta u_{\beta }^{0}+n_{\alpha }~M_{\alpha \beta ,\beta }~\delta w^{0}-n_{\beta }~M_{\alpha \beta }~\delta w_{,\alpha }^{0}\right]~\mathrm {d} s\right\}\mathrm {d} t$ Интеграция по частям и предположение о нулевой вариации на границе срединной поверхности дает $\delta U=-\int _{0}^{T}\left\{\int _{\Omega ^{0}}\left[N_{\alpha \beta ,\alpha }~\delta u_{\beta }^{0}+M_{\alpha \beta ,\beta \alpha }~\delta w^{0}\right]~\mathrm {d} A-\int _{\Gamma ^{0}}\left[n_{\alpha }~N_{\alpha \beta }~\delta u_{\beta }^{0}+n_{\alpha }~M_{\alpha \beta ,\beta }~\delta w^{0}+n_{\beta }~M_{\alpha \beta ,\alpha }~\delta w^{0}\right]~\mathrm {d} s\right\}\mathrm {d} t$ Если имеется внешняя распределенная сила $q(x,t)$ действуя по нормали к поверхности пластины, то виртуальная внешняя работа $\delta V_{\mathrm {ext} }=\int _{0}^{T}\left[\int _{\Omega ^{0}}q(x,t)~\delta w^{0}~\mathrm {d} A\right]\mathrm {d} t$ Из принципа виртуальной работы $\delta U+\delta V_{\mathrm {ext} }=\delta K$. Таким образом, основные уравнения баланса для пластины ${\begin{aligned}N_{\alpha \beta ,\beta }&=J_{1}~{\ddot {u}}_{\alpha }^{0}\\M_{\alpha \beta ,\alpha \beta }-q(x,t)&=J_{1}~{\ddot {w}}^{0}-J_{3}~{\ddot {w}}_{,\alpha \alpha }^{0}\end{aligned}}$

Решения этих уравнений для некоторых частных случаев можно найти в статье о колебаниях пластин. На рисунках ниже показаны некоторые колебательные моды для круглой пластины защемлённой по контуру.

• 
  режим k = 0, p = 1
• 
  режим k = 0, p = 2
• 
  режим k = 1, p = 2

Изотропные пластины

Основные уравнения значительно упрощаются для изотропных и однородных пластин, для которых деформациями в срединной плоскости можно пренебречь. В этом случае остается одно уравнение следующего вида (в прямоугольных декартовых координатах):

$D\,\left({\frac {\partial ^{4}w}{\partial x^{4}}}+2{\frac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\frac {\partial ^{4}w}{\partial y^{4}}}\right)=-q(x,y,t)-2\rho h\,{\frac {\partial ^{2}w}{\partial t^{2}}}\,.$

где $D$ — изгибная жесткость. Для однородной плиты толщиной $2h$ ,

$D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\,.$

В прямой записи

$D\,\nabla ^{2}\nabla ^{2}w=-q(x,y,t)-2\rho h\,{\ddot {w}}\,.$

Для свободных колебаний основное уравнение принимает вид

$D\,\nabla ^{2}\nabla ^{2}w=-2\rho h\,{\ddot {w}}\,.$

Вывод динамических уравнений для изотропных пластин Кирхгофа — Лява

Для изотропной и однородной пластины, соотношения напряжения-деформации ${\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}\,.$ где $\varepsilon _{\alpha \beta }$ задаются в плоскости пластины. Соотногения деформации-перемещения в теории Кирхгофа — Лява $\varepsilon _{\alpha \beta }={\frac {1}{2}}(u_{\alpha ,\beta }+u_{\beta ,\alpha })-x_{3}\,w_{,\alpha \beta }\,.$ Таким образом, в результирующие моменты, соответствующие этим перемещениям ${\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}w_{,11}\\w_{,22}\\w_{,12}\end{bmatrix}}$ Основные уравнение для изотропной и однородной пластины однородной толщины $2h$ при отсутствии перемещений в срединной плоскости $M_{11,11}+2M_{12,12}+M_{22,22}-q(x,t)=2\rho h{\ddot {w}}-{\frac {2}{3}}\rho h^{3}\left({\ddot {w}}_{,11}+{\ddot {w}}_{,22}+{\ddot {w}}_{,33}\right)\,.$ Дифференциация выражений для моментов даёт ${\begin{aligned}M_{11,11}&=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\left(w_{,1111}+\nu ~w_{,2211}\right)\\M_{22,22}&=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\left(\nu ~w_{,1122}+w_{,2222}\right)\\M_{12,12}&=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}(1-\nu )~w_{,1212}\end{aligned}}$ Подставление в основные уравнения приходим к ${\begin{aligned}-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}&\left(w_{,1111}+\nu ~w_{,2211}+2(1-\nu )~w_{,1212}+\nu ~w_{,1122}+w_{,2222}\right)=\\&q(x,t)+2\rho h{\ddot {w}}-{\frac {2}{3}}\rho h^{3}\left({\ddot {w}}_{,11}+{\ddot {w}}_{,22}+{\ddot {w}}_{,33}\right)\,.\end{aligned}}$ Поскольку порядок дифференциации не имеет значения, то $w_{,2211}=w_{,1212}=w_{,1122}$. Отсюда ${\begin{aligned}-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}&\left(w_{,1111}+2w_{,1212}+w_{,2222}\right)=\\&q(x,t)+2\rho h{\ddot {w}}-{\frac {2}{3}}\rho h^{3}\left({\ddot {w}}_{,11}+{\ddot {w}}_{,22}+{\ddot {w}}_{,33}\right)\,.\end{aligned}}$ Если жёсткость пластины определим как $D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}$ то $D\left(w_{,1111}+2w_{,1212}+w_{,2222}\right)=-q(x,t)-2\rho h{\ddot {w}}+{\frac {2}{3}}\rho h^{3}\left({\ddot {w}}_{,11}+{\ddot {w}}_{,22}+{\ddot {w}}_{,33}\right)\,.$ Для небольших деформаций, мы часто пренебрегаем пространственными производными поперечного ускорения пластины, тогда $D\left(w_{,1111}+2w_{,1212}+w_{,2222}\right)=-q(x,t)-2\rho h{\ddot {w}}\,.$ Тошда в прямой тенсорной нотации, основное уравнение для пластин $D\nabla ^{2}\nabla ^{2}w=-q(x,y,t)-2\rho h{\ddot {w}}\,.$