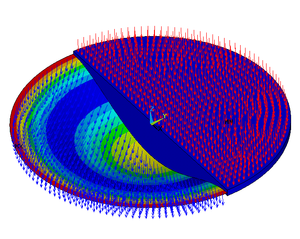
Изгиб круглой пластины с закреплёнными краями под действием пореречной силы. Левая половина пластины показывает деформированную форму, а правая половина — недеформированную. Этот расчет произведён с использованием программы Ansys . Изгиб пластин в теории упругости относится к расчёту деформаций в пластинах (в общем случае произвольной толщины, но малым по сравнению с продольными размерами), под действием перпендикулярных к плоскости пластины внешних сил и моментов. Величину отклонения можно определить, решив дифференциальные уравнения соответствующей теории пластин в зависимости от допущений на малость тех или иных параметров. По этим прогибам можно рассчитать напряжения в пластине. При известных напряжениях можно использовать теорию разрушения, чтобы определить, нарушение целостности плиты при данной нагрузке. Деформация пластины является функцией двух координат, поэтому теория пластин формулируется в общем случае в терминах дифференциальных уравнений в двумерном пространстве. Также считается, что пластина изначально (в ненапряжённом состоянии) имеет плоскую форму.
Силы и моменты действующие на плоской пластины для рассчёта равновесия элементарного объёма Для тонкой прямоугольной пластины толщиной
H
{\displaystyle H}
E
{\displaystyle E}
ν
{\displaystyle \nu }
w
{\displaystyle w}
В декартовой системе координат жёсткость при изгибе определяется
D
=
E
H
3
12
(
1
−
ν
2
)
.
{\displaystyle D={\frac {EH^{3}}{12\left(1-\nu ^{2}\right)}}.}
Изгибные моменты на единицу длины задаются[ 1]
M
x
=
−
D
(
∂
2
w
∂
x
2
+
ν
∂
2
w
∂
y
2
)
,
{\displaystyle M_{x}=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu {\frac {\partial ^{2}w}{\partial y^{2}}}\right),}
M
y
=
−
D
(
ν
∂
2
w
∂
x
2
+
∂
2
w
∂
y
2
)
.
{\displaystyle M_{y}=-D\left(\nu {\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right).}
Крутящий момент на единицу длины определяется
M
x
y
=
−
D
(
1
−
ν
)
∂
2
w
∂
x
∂
y
.
{\displaystyle M_{xy}=-D\left(1-\nu \right){\frac {\partial ^{2}w}{\partial x\partial y}}.}
Сдвиговые силы на единицу длины определяются выражением[ 2]
Q
x
=
−
D
∂
∂
x
(
∂
2
w
∂
x
2
+
∂
2
w
∂
y
2
)
,
{\displaystyle Q_{x}=-D{\frac {\partial }{\partial x}}\left({\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right),}
Q
y
=
−
D
∂
∂
y
(
∂
2
w
∂
x
2
+
∂
2
w
∂
y
2
)
.
{\displaystyle Q_{y}=-D{\frac {\partial }{\partial y}}\left({\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right).}
Компоненты изгибных напряжений определяются выражением
σ
x
=
−
12
D
z
H
3
(
∂
2
w
∂
x
2
+
ν
∂
2
w
∂
y
2
)
,
{\displaystyle \sigma _{x}=-{\frac {12Dz}{H^{3}}}\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu {\frac {\partial ^{2}w}{\partial y^{2}}}\right),}
σ
y
=
−
12
D
z
H
3
(
ν
∂
2
w
∂
x
2
+
∂
2
w
∂
y
2
)
.
{\displaystyle \sigma _{y}=-{\frac {12Dz}{H^{3}}}\left(\nu {\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right).}
Напряжение сдвига задается
τ
x
y
=
−
12
D
z
H
3
(
1
−
ν
)
∂
2
w
∂
x
∂
y
.
{\displaystyle \tau _{xy}=-{\frac {12Dz}{H^{3}}}\left(1-\nu \right){\frac {\partial ^{2}w}{\partial x\partial y}}.}
Изгибающие деформации в теории для малых отклонений определяются
ϵ
x
=
∂
u
∂
x
=
−
z
∂
2
w
∂
x
2
,
{\displaystyle \epsilon _{x}={\frac {\partial u}{\partial x}}=-z{\frac {\partial ^{2}w}{\partial x^{2}}},}
ϵ
y
=
∂
v
∂
y
=
−
z
∂
2
w
∂
y
2
.
{\displaystyle \epsilon _{y}={\frac {\partial v}{\partial y}}=-z{\frac {\partial ^{2}w}{\partial y^{2}}}.}
Деформации сдвига в теории для малых отклонений задаются
γ
x
y
=
∂
u
∂
y
+
∂
v
∂
x
=
−
2
z
∂
2
w
∂
x
∂
y
.
{\displaystyle \gamma _{xy}={\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}=-2z{\frac {\partial ^{2}w}{\partial x\partial y}}.}
В теории для больших отклонений пластин рассматривают деформации мембран в виде
ϵ
x
=
∂
u
∂
x
+
1
2
(
∂
w
∂
x
)
2
,
{\displaystyle \epsilon _{x}={\frac {\partial u}{\partial x}}+{\frac {1}{2}}\left({\frac {\partial w}{\partial x}}\right)^{2},}
ϵ
y
=
∂
v
∂
y
+
1
2
(
∂
w
∂
y
)
2
,
{\displaystyle \epsilon _{y}={\frac {\partial v}{\partial y}}+{\frac {1}{2}}\left({\frac {\partial w}{\partial y}}\right)^{2},}
γ
x
y
=
∂
u
∂
y
+
∂
v
∂
x
+
∂
w
∂
x
∂
w
∂
y
.
{\displaystyle \gamma _{xy}={\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}+{\frac {\partial w}{\partial x}}{\frac {\partial w}{\partial y}}.}
Эти прогибы определяются
u
=
−
z
∂
w
∂
x
,
{\displaystyle u=-z{\frac {\partial w}{\partial x}},}
v
=
−
z
∂
w
∂
y
.
{\displaystyle v=-z{\frac {\partial w}{\partial y}}.}
В теории пластин Кирхгофа — Лява система определяющих уравнений состоит из[ 3]
N
α
β
,
α
=
0
{\displaystyle N_{\alpha \beta ,\alpha }=0}
и
M
α
β
,
α
β
−
q
=
0.
{\displaystyle M_{\alpha \beta ,\alpha \beta }-q=0.}
Или в развёрнутой (координатной) форме
∂
N
11
∂
x
1
+
∂
N
21
∂
x
2
=
0
;
∂
N
12
∂
x
1
+
∂
N
22
∂
x
2
=
0
,
{\displaystyle {\cfrac {\partial N_{11}}{\partial x_{1}}}+{\cfrac {\partial N_{21}}{\partial x_{2}}}=0~;~~{\cfrac {\partial N_{12}}{\partial x_{1}}}+{\cfrac {\partial N_{22}}{\partial x_{2}}}=0,}
и
∂
2
M
11
∂
x
1
2
+
2
∂
2
M
12
∂
x
1
∂
x
2
+
∂
2
M
22
∂
x
2
2
=
q
.
{\displaystyle {\cfrac {\partial ^{2}M_{11}}{\partial x_{1}^{2}}}+2{\cfrac {\partial ^{2}M_{12}}{\partial x_{1}\partial x_{2}}}+{\cfrac {\partial ^{2}M_{22}}{\partial x_{2}^{2}}}=q.}
где
q
(
x
)
{\displaystyle q(x)}
H
=
2
h
{\displaystyle H=2h}
σ
i
j
{\displaystyle \sigma _{ij}}
N
α
β
:=
∫
−
h
h
σ
α
β
d
x
3
;
M
α
β
:=
∫
−
h
h
x
3
σ
α
β
d
x
3
.
{\displaystyle N_{\alpha \beta }:=\int _{-h}^{h}\sigma _{\alpha \beta }~dx_{3}~;~~M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}~.}
Величина
N
{\displaystyle N}
M
{\displaystyle M}
Для изотропных, однородных пластин с модулем Юнга
E
{\displaystyle E}
ν
{\displaystyle \nu }
[ 4]
∇
2
∇
2
w
=
−
q
D
;
D
:=
2
h
3
E
3
(
1
−
ν
2
)
=
H
3
E
12
(
1
−
ν
2
)
{\displaystyle \nabla ^{2}\nabla ^{2}w=-{\cfrac {q}{D}}~;~~D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}={\cfrac {H^{3}E}{12(1-\nu ^{2})}}}
где
w
(
x
1
,
x
2
)
{\displaystyle w(x_{1},x_{2})}
Малые прогибы тонких прямоугольных пластин описываются уравнением тонкой пластины Жермен — Лагранжа
∂
4
w
∂
x
4
+
2
∂
4
w
∂
x
2
∂
y
2
+
∂
4
w
∂
y
4
=
q
D
.
{\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {q}{D}}.}
Это уравнение было впервые выведено Лагранжем в декабре 1811 г. который исправил доклад Софи Жермен .
Большой прогиб тонких прямоугольных пластин описывается уравнениями для пластины Феппля — фон Кармана
∂
4
F
∂
x
4
+
2
∂
4
F
∂
x
2
∂
y
2
+
∂
4
F
∂
y
4
=
E
[
(
∂
2
w
∂
x
∂
y
)
2
−
∂
2
w
∂
x
2
∂
2
w
∂
y
2
]
,
{\displaystyle {\cfrac {\partial ^{4}F}{\partial x^{4}}}+2{\cfrac {\partial ^{4}F}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}F}{\partial y^{4}}}=E\left[\left({\cfrac {\partial ^{2}w}{\partial x\partial y}}\right)^{2}-{\cfrac {\partial ^{2}w}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}}\right],}
∂
4
w
∂
x
4
+
2
∂
4
w
∂
x
2
∂
y
2
+
∂
4
w
∂
y
4
=
q
D
+
H
D
(
∂
2
F
∂
y
2
∂
2
w
∂
x
2
+
∂
2
F
∂
x
2
∂
2
w
∂
y
2
−
2
∂
2
F
∂
x
∂
y
∂
2
w
∂
x
∂
y
)
,
{\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {q}{D}}+{\cfrac {H}{D}}\left({\cfrac {\partial ^{2}F}{\partial y^{2}}}{\cfrac {\partial ^{2}w}{\partial x^{2}}}+{\cfrac {\partial ^{2}F}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}}-2{\cfrac {\partial ^{2}F}{\partial x\partial y}}{\cfrac {\partial ^{2}w}{\partial x\partial y}}\right),}
где
F
{\displaystyle F}
Изгиб круглых пластин можно изучить, решив основное уравнение с соответствующими граничными условиями. Эти решения были впервые найдены Пуассоном в 1829 году. Для таких задач удобны цилиндрические координаты. z расстояние точки от средней плоскости пластины.
Основное уравнение в безкоординатной форме имеет вид
∇
2
∇
2
w
=
−
q
D
.
{\displaystyle \nabla ^{2}\nabla ^{2}w=-{\frac {q}{D}}\,.}
В цилиндрических координатах
(
r
,
θ
,
z
)
{\displaystyle (r,\theta ,z)}
∇
2
w
≡
1
r
∂
∂
r
(
r
∂
w
∂
r
)
+
1
r
2
∂
2
w
∂
θ
2
+
∂
2
w
∂
z
2
.
{\displaystyle \nabla ^{2}w\equiv {\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial w}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}w}{\partial \theta ^{2}}}+{\frac {\partial ^{2}w}{\partial z^{2}}}\,.}
Для симметрично нагруженных круглых пластин, где изгиб зависит от только радиуса
w
=
w
(
r
)
{\displaystyle w=w(r)}
∇
2
w
≡
1
r
d
d
r
(
r
d
w
d
r
)
.
{\displaystyle \nabla ^{2}w\equiv {\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\,.}
Следовательно, основное уравнение приобретёт вид обыкновенного дифференциального уравнения[ 5]
1
r
d
d
r
[
r
d
d
r
{
1
r
d
d
r
(
r
d
w
d
r
)
}
]
=
−
q
D
.
{\displaystyle {\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,.}
Если
q
{\displaystyle q}
D
{\displaystyle D}
w
(
r
)
=
−
q
r
4
64
D
+
C
1
ln
r
+
C
2
r
2
2
+
C
3
r
2
4
(
2
ln
r
−
1
)
+
C
4
{\displaystyle w(r)=-{\frac {qr^{4}}{64D}}+C_{1}\ln r+{\cfrac {C_{2}r^{2}}{2}}+{\cfrac {C_{3}r^{2}}{4}}(2\ln r-1)+C_{4}}
где
C
i
{\displaystyle C_{i}}
ϕ
(
r
)
=
d
w
d
r
=
−
q
r
3
16
D
+
C
1
r
+
C
2
r
+
C
3
r
ln
r
.
{\displaystyle \phi (r)={\cfrac {dw}{dr}}=-{\frac {qr^{3}}{16D}}+{\frac {C_{1}}{r}}+C_{2}r+C_{3}r\ln r\,.}
Для круглой пластины требование конечности прогиба и крутизны прогиба при
r
=
0
{\displaystyle r=0}
C
1
=
0
{\displaystyle C_{1}=0}
C
3
{\displaystyle C_{3}}
r
ln
r
{\displaystyle r\ln r\,}
r
=
0
{\displaystyle r=0}
Для круглой пластины (радиуса a ) с зажатыми краями
w
(
a
)
=
0
{\displaystyle w(a)=0}
ϕ
(
a
)
=
0
{\displaystyle \phi (a)=0}
[ 6]
w
(
r
)
=
−
q
64
D
(
a
2
−
r
2
)
2
and
ϕ
(
r
)
=
q
r
16
D
(
a
2
−
r
2
)
.
{\displaystyle w(r)=-{\frac {q}{64D}}(a^{2}-r^{2})^{2}\quad {\text{and}}\quad \phi (r)={\frac {qr}{16D}}(a^{2}-r^{2})\,.}
Смещения пластины в плоскости равны
u
r
(
r
)
=
−
z
ϕ
(
r
)
and
u
θ
(
r
)
=
0
.
{\displaystyle u_{r}(r)=-z\phi (r)\quad {\text{and}}\quad u_{\theta }(r)=0\,.}
Плоские деформации в пластине равны
ε
r
r
=
d
u
r
d
r
=
−
q
z
16
D
(
a
2
−
3
r
2
)
,
ε
θ
θ
=
u
r
r
=
−
q
z
16
D
(
a
2
−
r
2
)
,
ε
r
θ
=
0
.
{\displaystyle \varepsilon _{rr}={\cfrac {du_{r}}{dr}}=-{\frac {qz}{16D}}(a^{2}-3r^{2})~,~~\varepsilon _{\theta \theta }={\frac {u_{r}}{r}}=-{\frac {qz}{16D}}(a^{2}-r^{2})~,~~\varepsilon _{r\theta }=0\,.}
Напряжения в плоскости пластины равны
σ
r
r
=
E
1
−
ν
2
[
ε
r
r
+
ν
ε
θ
θ
]
;
σ
θ
θ
=
E
1
−
ν
2
[
ε
θ
θ
+
ν
ε
r
r
]
;
σ
r
θ
=
0
.
{\displaystyle \sigma _{rr}={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{rr}+\nu \varepsilon _{\theta \theta }\right]~;~~\sigma _{\theta \theta }={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{\theta \theta }+\nu \varepsilon _{rr}\right]~;~~\sigma _{r\theta }=0\,.}
Для плиты толщиной
2
h
{\displaystyle 2h}
D
=
2
E
h
3
/
[
3
(
1
−
ν
2
)
]
{\displaystyle D=2Eh^{3}/[3(1-\nu ^{2})]}
σ
r
r
=
−
3
q
z
32
h
3
[
(
1
+
ν
)
a
2
−
(
3
+
ν
)
r
2
]
σ
θ
θ
=
−
3
q
z
32
h
3
[
(
1
+
ν
)
a
2
−
(
1
+
3
ν
)
r
2
]
σ
r
θ
=
0
.
{\displaystyle {\begin{aligned}\sigma _{rr}&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]\\\sigma _{\theta \theta }&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]\\\sigma _{r\theta }&=0\,.\end{aligned}}}
Результирующие моменты (изгибные моменты) равны
M
r
r
=
−
q
16
[
(
1
+
ν
)
a
2
−
(
3
+
ν
)
r
2
]
;
M
θ
θ
=
−
q
16
[
(
1
+
ν
)
a
2
−
(
1
+
3
ν
)
r
2
]
;
M
r
θ
=
0
.
{\displaystyle M_{rr}=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]~;~~M_{\theta \theta }=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]~;~~M_{r\theta }=0\,.}
Максимальное радиальное напряжение при
z
=
h
{\displaystyle z=h}
r
=
a
{\displaystyle r=a}
σ
r
r
|
z
=
h
,
r
=
a
=
3
q
a
2
16
h
2
=
3
q
a
2
4
H
2
{\displaystyle \left.\sigma _{rr}\right|_{z=h,r=a}={\frac {3qa^{2}}{16h^{2}}}={\frac {3qa^{2}}{4H^{2}}}}
где
H
:=
2
h
{\displaystyle H:=2h}
[ 7]
M
r
r
|
r
=
a
=
q
a
2
8
,
M
θ
θ
|
r
=
a
=
ν
q
a
2
8
,
M
r
r
|
r
=
0
=
M
θ
θ
|
r
=
0
=
−
(
1
+
ν
)
q
a
2
16
.
{\displaystyle \left.M_{rr}\right|_{r=a}={\frac {qa^{2}}{8}}~,~~\left.M_{\theta \theta }\right|_{r=a}={\frac {\nu qa^{2}}{8}}~,~~\left.M_{rr}\right|_{r=0}=\left.M_{\theta \theta }\right|_{r=0}=-{\frac {(1+\nu )qa^{2}}{16}}\,.}
[ 8]
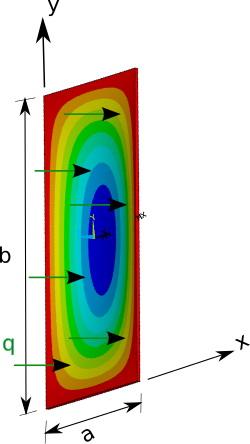
Изгиб прямоугольной пластины под действием распределенной силы
q
{\displaystyle q}
Для прямоугольных пластин Навье в 1820 году ввел простой метод определения смещения и напряжения, когда пластина опирается на края. Идея заключалась в том, чтобы выразить приложенную нагрузку в терминах компонент ряда Фурье, найти решение для синусоидальной нагрузки (одна гармоника Фурье), а затем сложить гармоники Фурье, чтобы получить решение для произвольной нагрузки.
Предположим, что нагрузка имеет вид[ 9]
q
(
x
,
y
)
=
q
0
sin
π
x
a
sin
π
y
b
.
{\displaystyle q(x,y)=q_{0}\sin {\frac {\pi x}{a}}\sin {\frac {\pi y}{b}}\,.}
Здесь
q
0
{\displaystyle q_{0}}
a
{\displaystyle a}
x
{\displaystyle x}
b
{\displaystyle b}
y
{\displaystyle y}
Поскольку пластина просто поддерживается на краях, то смещение
w
(
x
,
y
)
{\displaystyle w(x,y)}
M
x
x
{\displaystyle M_{xx}}
x
=
0
{\displaystyle x=0}
x
=
a
{\displaystyle x=a}
M
y
y
{\displaystyle M_{yy}}
y
=
0
{\displaystyle y=0}
y
=
b
{\displaystyle y=b}
При этих граничные условиях и решение уравнения для пластины имеет вид[ 10]
w
(
x
,
y
)
=
q
0
π
4
D
(
1
a
2
+
1
b
2
)
−
2
sin
π
x
a
sin
π
y
b
.
{\displaystyle w(x,y)={\frac {q_{0}}{\pi ^{4}D}}\,\left({\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}\right)^{-2}\,\sin {\frac {\pi x}{a}}\sin {\frac {\pi y}{b}}\,.}
Где D жесткость на изгиб
D
=
E
t
3
12
(
1
−
ν
2
)
.
{\displaystyle D={\frac {Et^{3}}{12(1-\nu ^{2})}}.}
Analogous to flexural stiffness EI.[ 11]
При общей нагрузки в виде
q
(
x
,
y
)
=
q
0
sin
m
π
x
a
sin
n
π
y
b
{\displaystyle q(x,y)=q_{0}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}
где
m
{\displaystyle m}
n
{\displaystyle n}
[ 12]
(1)
w
(
x
,
y
)
=
q
0
π
4
D
(
m
2
a
2
+
n
2
b
2
)
−
2
sin
m
π
x
a
sin
n
π
y
b
.
{\displaystyle {\text{(1)}}\qquad w(x,y)={\frac {q_{0}}{\pi ^{4}D}}\,\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{-2}\,\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,.}
Определяем общую нагрузку
q
(
x
,
y
)
{\displaystyle q(x,y)}
[ 12]
q
(
x
,
y
)
=
∑
m
=
1
∞
∑
n
=
1
∞
a
m
n
sin
m
π
x
a
sin
n
π
y
b
{\displaystyle q(x,y)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }a_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}
где
a
m
n
{\displaystyle a_{mn}}
[ 13]
a
m
n
=
4
a
b
∫
0
b
∫
0
a
q
(
x
,
y
)
sin
m
π
x
a
sin
n
π
y
b
d
x
d
y
{\displaystyle a_{mn}={\frac {4}{ab}}\int _{0}^{b}\int _{0}^{a}q(x,y)\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,{\text{d}}x{\text{d}}y}
Таким образом, классическое уравнение прямоугольной пластины для малых прогибов принимает следующий вид:
∂
4
w
∂
x
4
+
2
∂
4
w
∂
x
2
∂
y
2
+
∂
4
w
∂
y
4
=
1
D
∑
m
=
1
∞
∑
n
=
1
∞
a
m
n
sin
m
π
x
a
sin
n
π
y
b
{\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {1}{D}}\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }a_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}
Предполагаем решение
w
(
x
,
y
)
{\displaystyle w(x,y)}
w
(
x
,
y
)
=
∑
m
=
1
∞
∑
n
=
1
∞
w
m
n
sin
m
π
x
a
sin
n
π
y
b
{\displaystyle w(x,y)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}
Частные дифференциалы этой функции даются выражениями
∂
4
w
∂
x
4
=
∑
m
=
1
∞
∑
n
=
1
∞
(
m
π
a
)
4
w
m
n
sin
m
π
x
a
sin
n
π
y
b
.
{\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {m\pi }{a}}\right)^{4}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}.}
∂
4
w
∂
x
2
∂
y
2
=
∑
m
=
1
∞
∑
n
=
1
∞
(
m
π
a
)
2
(
n
π
b
)
2
w
m
n
sin
m
π
x
a
sin
n
π
y
b
,
{\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {m\pi }{a}}\right)^{2}\left({\frac {n\pi }{b}}\right)^{2}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}},}
∂
4
w
∂
y
4
=
∑
m
=
1
∞
∑
n
=
1
∞
(
n
π
b
)
4
w
m
n
sin
m
π
x
a
sin
n
π
y
b
.
{\displaystyle {\cfrac {\partial ^{4}w}{\partial y^{4}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {n\pi }{b}}\right)^{4}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}.}
Подставляя эти выражения в уравнение для пластины, получим
∑
m
=
1
∞
∑
n
=
1
∞
(
(
m
π
a
)
2
+
(
n
π
b
)
2
)
2
w
m
n
sin
m
π
x
a
sin
n
π
y
b
=
∑
m
=
1
∞
∑
n
=
1
∞
a
m
n
D
sin
m
π
x
a
sin
n
π
y
b
{\displaystyle \sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left(\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}\right)^{2}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\cfrac {a_{mn}}{D}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}
Приравнивая два ряда получим для коэффициентов
(
(
m
π
a
)
2
+
(
n
π
b
)
2
)
2
w
m
n
=
a
m
n
D
{\displaystyle \left(\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}\right)^{2}w_{mn}={\cfrac {a_{mn}}{D}}}
или при перестановки получим
w
m
n
=
1
π
4
D
a
m
n
(
m
2
a
2
+
n
2
b
2
)
2
{\displaystyle w_{mn}={\frac {1}{\pi ^{4}D}}{\frac {a_{mn}}{\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}}
Прогиб свободно опертой пластины (на углах) при общей нагрузке задаётся выражением[ 13]
w
(
x
,
y
)
=
1
π
4
D
∑
m
=
1
∞
∑
n
=
1
∞
a
m
n
(
m
2
a
2
+
n
2
b
2
)
2
sin
m
π
x
a
sin
n
π
y
b
{\displaystyle w(x,y)={\frac {1}{\pi ^{4}D}}\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {a_{mn}}{\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}
Для равномерно распределенной нагрузки имеем
q
(
x
,
y
)
=
q
0
{\displaystyle q(x,y)=q_{0}}
Таким образом, соответствующий коэффициент Фурье определяется выражением
a
m
n
=
4
a
b
∫
0
a
∫
0
b
q
0
sin
m
π
x
a
sin
n
π
y
b
d
x
d
y
{\displaystyle a_{mn}={\frac {4}{ab}}\int _{0}^{a}\int _{0}^{b}q_{0}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,{\text{d}}x{\text{d}}y}
Вычисляя двойной интеграл, имеем
a
m
n
=
4
q
0
π
2
m
n
(
1
−
cos
m
π
)
(
1
−
cos
n
π
)
{\displaystyle a_{mn}={\frac {4q_{0}}{\pi ^{2}mn}}(1-\cos m\pi )(1-\cos n\pi )}
или в другом виде кусочно-заданной функции
a
m
n
=
{
16
q
0
π
2
m
n
m
and
n
odd
0
m
or
n
even
{\displaystyle a_{mn}={\begin{cases}{\cfrac {16q_{0}}{\pi ^{2}mn}}&m~{\text{and}}~n~{\text{odd}}\\0&m~{\text{or}}~n~{\text{even}}\end{cases}}}
Прогиб свободно опертой пластины (с условиями на углах) с равномерно распределенной нагрузкой определяется выражением
w
(
x
,
y
)
=
16
q
0
π
6
D
∑
m
=
1
,
3
,
5
,
.
.
.
∞
∑
n
=
1
,
3
,
5
,
.
.
.
∞
1
m
n
(
m
2
a
2
+
n
2
b
2
)
2
sin
m
π
x
a
sin
n
π
y
b
{\displaystyle w(x,y)={\frac {16q_{0}}{\pi ^{6}D}}\sum _{m=1,3,5,...}^{\infty }\sum _{n=1,3,5,...}^{\infty }{\frac {1}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}
Изгибающие моменты на единицу длины в пластине определяются выражением
M
x
=
16
q
0
π
4
∑
m
=
1
,
3
,
5
,
.
.
.
∞
∑
n
=
1
,
3
,
5
,
.
.
.
∞
m
2
a
2
+
ν
n
2
b
2
m
n
(
m
2
a
2
+
n
2
b
2
)
2
sin
m
π
x
a
sin
n
π
y
b
{\displaystyle M_{x}={\frac {16q_{0}}{\pi ^{4}}}\sum _{m=1,3,5,...}^{\infty }\sum _{n=1,3,5,...}^{\infty }{\frac {{\frac {m^{2}}{a^{2}}}+\nu {\frac {n^{2}}{b^{2}}}}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}
M
y
=
16
q
0
π
4
∑
m
=
1
,
3
,
5
,
.
.
.
∞
∑
n
=
1
,
3
,
5
,
.
.
.
∞
n
2
b
2
+
ν
m
2
a
2
m
n
(
m
2
a
2
+
n
2
b
2
)
2
sin
m
π
x
a
sin
n
π
y
b
{\displaystyle M_{y}={\frac {16q_{0}}{\pi ^{4}}}\sum _{m=1,3,5,...}^{\infty }\sum _{n=1,3,5,...}^{\infty }{\frac {{\frac {n^{2}}{b^{2}}}+\nu {\frac {m^{2}}{a^{2}}}}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}}
Другой подход был предложен Леви[ 14]
∇
2
∇
2
w
=
q
/
D
{\displaystyle \nabla ^{2}\nabla ^{2}w=q/D}
Y
m
(
y
)
{\displaystyle Y_{m}(y)}
y
=
0
{\displaystyle y=0}
y
=
b
{\displaystyle y=b}
Предположим, что[ 15]
w
(
x
,
y
)
=
∑
m
=
1
∞
Y
m
(
y
)
sin
m
π
x
a
.
{\displaystyle w(x,y)=\sum _{m=1}^{\infty }Y_{m}(y)\sin {\frac {m\pi x}{a}}\,.}
Для пластины, которая свободно опирается краями при
x
=
0
{\displaystyle x=0}
x
=
a
{\displaystyle x=a}
w
=
0
{\displaystyle w=0}
M
x
x
=
0
{\displaystyle M_{xx}=0}
∂
w
/
∂
y
=
0
{\displaystyle \partial w/\partial y=0}
∂
2
w
/
∂
y
2
=
0
{\displaystyle \partial ^{2}w/\partial y^{2}=0}
∂
2
w
/
∂
x
2
=
0
{\displaystyle \partial ^{2}w/\partial x^{2}=0}
Рассмотрим случай чисто моментной нагрузки. В этом случае
q
=
0
{\displaystyle q=0}
w
(
x
,
y
)
{\displaystyle w(x,y)}
∇
2
∇
2
w
=
0
{\displaystyle \nabla ^{2}\nabla ^{2}w=0}
∂
4
w
∂
x
4
+
2
∂
4
w
∂
x
2
∂
y
2
+
∂
4
w
∂
y
4
=
0
.
{\displaystyle {\frac {\partial ^{4}w}{\partial x^{4}}}+2{\frac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\frac {\partial ^{4}w}{\partial y^{4}}}=0\,.}
Подставляем выражение для
w
(
x
,
y
)
{\displaystyle w(x,y)}
[ 16]
∑
m
=
1
∞
[
(
m
π
a
)
4
Y
m
sin
m
π
x
a
−
2
(
m
π
a
)
2
d
2
Y
m
d
y
2
sin
m
π
x
a
+
d
4
Y
m
d
y
4
sin
m
π
x
a
]
=
0
{\displaystyle \sum _{m=1}^{\infty }\left[\left({\frac {m\pi }{a}}\right)^{4}Y_{m}\sin {\frac {m\pi x}{a}}-2\left({\frac {m\pi }{a}}\right)^{2}{\cfrac {d^{2}Y_{m}}{dy^{2}}}\sin {\frac {m\pi x}{a}}+{\frac {d^{4}Y_{m}}{dy^{4}}}\sin {\frac {m\pi x}{a}}\right]=0}
или
d
4
Y
m
d
y
4
−
2
m
2
π
2
a
2
d
2
Y
m
d
y
2
+
m
4
π
4
a
4
Y
m
=
0
.
{\displaystyle {\frac {d^{4}Y_{m}}{dy^{4}}}-2{\frac {m^{2}\pi ^{2}}{a^{2}}}{\cfrac {d^{2}Y_{m}}{dy^{2}}}+{\frac {m^{4}\pi ^{4}}{a^{4}}}Y_{m}=0\,.}
Это обыкновенное дифференциальное уравнение, имеющее общее решение[ 17]
Y
m
=
A
m
cosh
m
π
y
a
+
B
m
m
π
y
a
cosh
m
π
y
a
+
C
m
sinh
m
π
y
a
+
D
m
m
π
y
a
sinh
m
π
y
a
{\displaystyle Y_{m}=A_{m}\cosh {\frac {m\pi y}{a}}+B_{m}{\frac {m\pi y}{a}}\cosh {\frac {m\pi y}{a}}+C_{m}\sinh {\frac {m\pi y}{a}}+D_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}}
где
A
m
,
B
m
,
C
m
,
D
m
{\displaystyle A_{m},B_{m},C_{m},D_{m}}
w
(
x
,
y
)
=
∑
m
=
1
∞
[
(
A
m
+
B
m
m
π
y
a
)
cosh
m
π
y
a
+
(
C
m
+
D
m
m
π
y
a
)
sinh
m
π
y
a
]
sin
m
π
x
a
.
{\displaystyle w(x,y)=\sum _{m=1}^{\infty }\left[\left(A_{m}+B_{m}{\frac {m\pi y}{a}}\right)\cosh {\frac {m\pi y}{a}}+\left(C_{m}+D_{m}{\frac {m\pi y}{a}}\right)\sinh {\frac {m\pi y}{a}}\right]\sin {\frac {m\pi x}{a}}\,.}
Выберем систему координат так, чтобы границы пластины находились на краях при
x
=
0
{\displaystyle x=0}
x
=
a
{\displaystyle x=a}
y
=
±
b
/
2
{\displaystyle y=\pm b/2}
y
=
±
b
/
2
{\displaystyle y=\pm b/2}
w
=
0
,
−
D
∂
2
w
∂
y
2
|
y
=
b
/
2
=
f
1
(
x
)
,
−
D
∂
2
w
∂
y
2
|
y
=
−
b
/
2
=
f
2
(
x
)
{\displaystyle w=0\,,-D{\frac {\partial ^{2}w}{\partial y^{2}}}{\Bigr |}_{y=b/2}=f_{1}(x)\,,-D{\frac {\partial ^{2}w}{\partial y^{2}}}{\Bigr |}_{y=-b/2}=f_{2}(x)}
где
f
1
(
x
)
,
f
2
(
x
)
{\displaystyle f_{1}(x),f_{2}(x)}
M
y
y
|
y
=
−
b
/
2
=
M
y
y
|
y
=
b
/
2
{\displaystyle M_{yy}{\Bigr |}_{y=-b/2}=M_{yy}{\Bigr |}_{y=b/2}}
и
f
1
(
x
)
=
f
2
(
x
)
=
∑
m
=
1
∞
E
m
sin
m
π
x
a
{\displaystyle f_{1}(x)=f_{2}(x)=\sum _{m=1}^{\infty }E_{m}\sin {\frac {m\pi x}{a}}}
получим[ 18]
w
(
x
,
y
)
=
a
2
2
π
2
D
∑
m
=
1
∞
E
m
m
2
cosh
α
m
sin
m
π
x
a
(
α
m
tanh
α
m
cosh
m
π
y
a
−
m
π
y
a
sinh
m
π
y
a
)
{\displaystyle w(x,y)={\frac {a^{2}}{2\pi ^{2}D}}\sum _{m=1}^{\infty }{\frac {E_{m}}{m^{2}\cosh \alpha _{m}}}\,\sin {\frac {m\pi x}{a}}\,\left(\alpha _{m}\tanh \alpha _{m}\cosh {\frac {m\pi y}{a}}-{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}\right)}
где
α
m
=
m
π
b
2
a
.
{\displaystyle \alpha _{m}={\frac {m\pi b}{2a}}\,.}
Аналогично для антисимметричного случая, когда
M
y
y
|
y
=
−
b
/
2
=
−
M
y
y
|
y
=
b
/
2
{\displaystyle M_{yy}{\Bigr |}_{y=-b/2}=-M_{yy}{\Bigr |}_{y=b/2}}
получим[ 19]
w
(
x
,
y
)
=
a
2
2
π
2
D
∑
m
=
1
∞
E
m
m
2
sinh
α
m
sin
m
π
x
a
(
α
m
coth
α
m
sinh
m
π
y
a
−
m
π
y
a
cosh
m
π
y
a
)
.
{\displaystyle w(x,y)={\frac {a^{2}}{2\pi ^{2}D}}\sum _{m=1}^{\infty }{\frac {E_{m}}{m^{2}\sinh \alpha _{m}}}\,\sin {\frac {m\pi x}{a}}\,\left(\alpha _{m}\coth \alpha _{m}\sinh {\frac {m\pi y}{a}}-{\frac {m\pi y}{a}}\cosh {\frac {m\pi y}{a}}\right)\,.}
Используя симметричные и антисимметричные решения, можно составить более общие решения.
Для равномерно распределенной нагрузки
q
(
x
,
y
)
=
q
0
{\displaystyle q(x,y)=q_{0}}
Отклонение опёртой пластины с центром при
(
a
2
,
0
)
{\displaystyle \left({\frac {a}{2}},0\right)}
[ 20]
w
(
x
,
y
)
=
q
0
a
4
D
∑
m
=
1
,
3
,
5
,
.
.
.
∞
(
A
m
cosh
m
π
y
a
+
B
m
m
π
y
a
sinh
m
π
y
a
+
G
m
)
sin
m
π
x
a
where
A
m
=
−
2
(
α
m
tanh
α
m
+
2
)
π
5
m
5
cosh
α
m
B
m
=
2
π
5
m
5
cosh
α
m
G
m
=
4
π
5
m
5
α
m
=
m
π
b
2
a
{\displaystyle {\begin{aligned}&w(x,y)={\frac {q_{0}a^{4}}{D}}\sum _{m=1,3,5,...}^{\infty }\left(A_{m}\cosh {\frac {m\pi y}{a}}+B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}+G_{m}\right)\sin {\frac {m\pi x}{a}}\\\\&{\begin{aligned}{\text{where}}\quad &A_{m}=-{\frac {2\left(\alpha _{m}\tanh \alpha _{m}+2\right)}{\pi ^{5}m^{5}\cosh \alpha _{m}}}\\&B_{m}={\frac {2}{\pi ^{5}m^{5}\cosh \alpha _{m}}}\\&G_{m}={\frac {4}{\pi ^{5}m^{5}}}\\\\\quad &\alpha _{m}={\frac {m\pi b}{2a}}\end{aligned}}\end{aligned}}}
Изгибающие моменты на единицу длины в пластине определяются выражениями
M
x
=
−
q
0
π
2
a
2
∑
m
=
1
,
3
,
5
,
.
.
.
∞
m
2
(
(
(
ν
−
1
)
A
m
+
2
ν
B
m
)
cosh
m
π
y
a
+
(
ν
−
1
)
B
m
m
π
y
a
sinh
m
π
y
a
−
G
m
)
sin
m
π
x
a
{\displaystyle M_{x}=-q_{0}\pi ^{2}a^{2}\sum _{m=1,3,5,...}^{\infty }m^{2}\left(\left(\left(\nu -1\right)A_{m}+2\nu B_{m}\right)\cosh {\frac {m\pi y}{a}}+\left(\nu -1\right)B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}-G_{m}\right)\sin {\frac {m\pi x}{a}}}
M
y
=
−
q
0
π
2
a
2
∑
m
=
1
,
3
,
5
,
.
.
.
∞
m
2
(
(
(
1
−
ν
)
A
m
+
2
B
m
)
cosh
m
π
y
a
+
(
1
−
ν
)
B
m
m
π
y
a
sinh
m
π
y
a
−
ν
G
m
)
sin
m
π
x
a
{\displaystyle M_{y}=-q_{0}\pi ^{2}a^{2}\sum _{m=1,3,5,...}^{\infty }m^{2}\left(\left(\left(1-\nu \right)A_{m}+2B_{m}\right)\cosh {\frac {m\pi y}{a}}+\left(1-\nu \right)B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}-\nu G_{m}\right)\sin {\frac {m\pi x}{a}}}
Для частного случая, когда нагрузка симметрична и момент однороден, при
y
=
±
b
/
2
{\displaystyle y=\pm b/2}
M
y
y
=
f
1
(
x
)
=
4
M
0
π
∑
m
=
1
∞
1
2
m
−
1
sin
(
2
m
−
1
)
π
x
a
.
{\displaystyle M_{yy}=f_{1}(x)={\frac {4M_{0}}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{2m-1}}\,\sin {\frac {(2m-1)\pi x}{a}}\,.}
Результирующий изгиб равен
w
(
x
,
y
)
=
2
M
0
a
2
π
3
D
∑
m
=
1
∞
1
(
2
m
−
1
)
3
cosh
α
m
sin
(
2
m
−
1
)
π
x
a
×
[
α
m
tanh
α
m
cosh
(
2
m
−
1
)
π
y
a
−
(
2
m
−
1
)
π
y
a
sinh
(
2
m
−
1
)
π
y
a
]
{\displaystyle {\begin{aligned}&w(x,y)={\frac {2M_{0}a^{2}}{\pi ^{3}D}}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)^{3}\cosh \alpha _{m}}}\sin {\frac {(2m-1)\pi x}{a}}\times \\&~~\left[\alpha _{m}\,\tanh \alpha _{m}\cosh {\frac {(2m-1)\pi y}{a}}-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}\right]\end{aligned}}}
где
α
m
=
π
(
2
m
−
1
)
b
2
a
.
{\displaystyle \alpha _{m}={\frac {\pi (2m-1)b}{2a}}\,.}
Изгибающие моменты и поперечные силы, соответствующие смещению
w
{\displaystyle w}
M
x
x
=
−
D
(
∂
2
w
∂
x
2
+
ν
∂
2
w
∂
y
2
)
=
2
M
0
(
1
−
ν
)
π
∑
m
=
1
∞
1
(
2
m
−
1
)
cosh
α
m
×
sin
(
2
m
−
1
)
π
x
a
×
[
−
(
2
m
−
1
)
π
y
a
sinh
(
2
m
−
1
)
π
y
a
+
{
2
ν
1
−
ν
+
α
m
tanh
α
m
}
cosh
(
2
m
−
1
)
π
y
a
]
M
x
y
=
(
1
−
ν
)
D
∂
2
w
∂
x
∂
y
=
−
2
M
0
(
1
−
ν
)
π
∑
m
=
1
∞
1
(
2
m
−
1
)
cosh
α
m
×
cos
(
2
m
−
1
)
π
x
a
×
[
(
2
m
−
1
)
π
y
a
cosh
(
2
m
−
1
)
π
y
a
+
(
1
−
α
m
tanh
α
m
)
sinh
(
2
m
−
1
)
π
y
a
]
Q
z
x
=
∂
M
x
x
∂
x
−
∂
M
x
y
∂
y
=
4
M
0
a
∑
m
=
1
∞
1
cosh
α
m
×
cos
(
2
m
−
1
)
π
x
a
cosh
(
2
m
−
1
)
π
y
a
.
{\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&={\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\sin {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.\left\{{\frac {2\nu }{1-\nu }}+\alpha _{m}\tanh \alpha _{m}\right\}\cosh {\frac {(2m-1)\pi y}{a}}\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&=-{\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[{\frac {(2m-1)\pi y}{a}}\cosh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.(1-\alpha _{m}\tanh \alpha _{m})\sinh {\frac {(2m-1)\pi y}{a}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {4M_{0}}{a}}\sum _{m=1}^{\infty }{\frac {1}{\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\cosh {\frac {(2m-1)\pi y}{a}}\,.\end{aligned}}}
Напряжения
σ
x
x
=
12
z
h
3
M
x
x
and
σ
z
x
=
1
κ
h
Q
z
x
(
1
−
4
z
2
h
2
)
.
{\displaystyle \sigma _{xx}={\frac {12z}{h^{3}}}\,M_{xx}\quad {\text{and}}\quad \sigma _{zx}={\frac {1}{\kappa h}}\,Q_{zx}\left(1-{\frac {4z^{2}}{h^{2}}}\right)\,.}
Цилиндрический изгиб возникает, когда прямоугольная пластина имеющая размеры
a
×
b
×
h
{\displaystyle a\times b\times h}
a
≪
b
{\displaystyle a\ll b}
h
{\displaystyle h}
С помощью методов Навье и Леви также можно найти решения для свободно опёртых пластин при цилиндрическом изгибе с различным количеством незакреплённых краёв[ 21]
Для толстых пластин необходимо учитывать влияние сдвиговых напряжений по толщине на ориентацию нормали к средней поверхности после деформации. Теория Миндлина предлагает единый подход к нахождению деформации и напряжений в таких пластинах. Решения теории Миндлина можно получить из эквивалентных решений Кирхгофа-Лява с использованием канонических соотношений[ 22]
Канонические уравнения для изотропных толстых пластин можно записать в виде[ 22]
∇
2
(
M
−
B
1
+
ν
q
)
=
−
q
κ
G
h
(
∇
2
w
+
M
D
)
=
−
(
1
−
B
c
2
1
+
ν
)
q
∇
2
(
∂
φ
1
∂
x
2
−
∂
φ
2
∂
x
1
)
=
c
2
(
∂
φ
1
∂
x
2
−
∂
φ
2
∂
x
1
)
{\displaystyle {\begin{aligned}&\nabla ^{2}\left({\mathcal {M}}-{\frac {\mathcal {B}}{1+\nu }}\,q\right)=-q\\&\kappa Gh\left(\nabla ^{2}w+{\frac {\mathcal {M}}{D}}\right)=-\left(1-{\cfrac {{\mathcal {B}}c^{2}}{1+\nu }}\right)q\\&\nabla ^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)=c^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)\end{aligned}}}
где
q
{\displaystyle q}
G
{\displaystyle G}
D
=
E
h
3
/
[
12
(
1
−
ν
2
)
]
{\displaystyle D=Eh^{3}/[12(1-\nu ^{2})]}
h
{\displaystyle h}
c
2
=
2
κ
G
h
/
[
D
(
1
−
ν
)
]
{\displaystyle c^{2}=2\kappa Gh/[D(1-\nu )]}
κ
{\displaystyle \kappa }
E
{\displaystyle E}
ν
{\displaystyle \nu }
M
=
D
[
A
(
∂
φ
1
∂
x
1
+
∂
φ
2
∂
x
2
)
−
(
1
−
A
)
∇
2
w
]
+
2
q
1
−
ν
2
B
.
{\displaystyle {\mathcal {M}}=D\left[{\mathcal {A}}\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)-(1-{\mathcal {A}})\nabla ^{2}w\right]+{\frac {2q}{1-\nu ^{2}}}{\mathcal {B}}\,.}
Согласно теории Миндлина
w
{\displaystyle w}
φ
1
{\displaystyle \varphi _{1}}
φ
2
{\displaystyle \varphi _{2}}
x
2
{\displaystyle x_{2}}
x
1
{\displaystyle x_{1}}
A
=
1
{\displaystyle {\mathcal {A}}=1}
B
=
0
{\displaystyle {\mathcal {B}}=0}
κ
{\displaystyle \kappa }
5
/
6
{\displaystyle 5/6}
Решения основных уравнений можно найти, если знать соответствующие решения Кирхгофа-Лява с помощью соотношений
w
=
w
K
+
M
K
κ
G
h
(
1
−
B
c
2
2
)
−
Φ
+
Ψ
φ
1
=
−
∂
w
K
∂
x
1
−
1
κ
G
h
(
1
−
1
A
−
B
c
2
2
)
Q
1
K
+
∂
∂
x
1
(
D
κ
G
h
A
∇
2
Φ
+
Φ
−
Ψ
)
+
1
c
2
∂
Ω
∂
x
2
φ
2
=
−
∂
w
K
∂
x
2
−
1
κ
G
h
(
1
−
1
A
−
B
c
2
2
)
Q
2
K
+
∂
∂
x
2
(
D
κ
G
h
A
∇
2
Φ
+
Φ
−
Ψ
)
+
1
c
2
∂
Ω
∂
x
1
{\displaystyle {\begin{aligned}w&=w^{K}+{\frac {{\mathcal {M}}^{K}}{\kappa Gh}}\left(1-{\frac {{\mathcal {B}}c^{2}}{2}}\right)-\Phi +\Psi \\\varphi _{1}&=-{\frac {\partial w^{K}}{\partial x_{1}}}-{\frac {1}{\kappa Gh}}\left(1-{\frac {1}{\mathcal {A}}}-{\frac {{\mathcal {B}}c^{2}}{2}}\right)Q_{1}^{K}+{\frac {\partial }{\partial x_{1}}}\left({\frac {D}{\kappa Gh{\mathcal {A}}}}\nabla ^{2}\Phi +\Phi -\Psi \right)+{\frac {1}{c^{2}}}{\frac {\partial \Omega }{\partial x_{2}}}\\\varphi _{2}&=-{\frac {\partial w^{K}}{\partial x_{2}}}-{\frac {1}{\kappa Gh}}\left(1-{\frac {1}{\mathcal {A}}}-{\frac {{\mathcal {B}}c^{2}}{2}}\right)Q_{2}^{K}+{\frac {\partial }{\partial x_{2}}}\left({\frac {D}{\kappa Gh{\mathcal {A}}}}\nabla ^{2}\Phi +\Phi -\Psi \right)+{\frac {1}{c^{2}}}{\frac {\partial \Omega }{\partial x_{1}}}\end{aligned}}}
где
w
K
{\displaystyle w^{K}}
Φ
{\displaystyle \Phi }
∇
2
∇
2
Φ
=
0
{\displaystyle \nabla ^{2}\nabla ^{2}\Phi =0}
Ψ
{\displaystyle \Psi }
∇
2
Ψ
=
0
{\displaystyle \nabla ^{2}\Psi =0}
M
=
M
K
+
B
1
+
ν
q
+
D
∇
2
Φ
;
M
K
:=
−
D
∇
2
w
K
Q
1
K
=
−
D
∂
∂
x
1
(
∇
2
w
K
)
,
Q
2
K
=
−
D
∂
∂
x
2
(
∇
2
w
K
)
Ω
=
∂
φ
1
∂
x
2
−
∂
φ
2
∂
x
1
,
∇
2
Ω
=
c
2
Ω
.
{\displaystyle {\begin{aligned}{\mathcal {M}}&={\mathcal {M}}^{K}+{\frac {\mathcal {B}}{1+\nu }}\,q+D\nabla ^{2}\Phi ~;~~{\mathcal {M}}^{K}:=-D\nabla ^{2}w^{K}\\Q_{1}^{K}&=-D{\frac {\partial }{\partial x_{1}}}\left(\nabla ^{2}w^{K}\right)~,~~Q_{2}^{K}=-D{\frac {\partial }{\partial x_{2}}}\left(\nabla ^{2}w^{K}\right)\\\Omega &={\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}~,~~\nabla ^{2}\Omega =c^{2}\Omega \,.\end{aligned}}}
Для свободно опертых пластин сумма моментов Маркуса равна нулю
M
=
1
1
+
ν
(
M
11
+
M
22
)
=
D
(
∂
φ
1
∂
x
1
+
∂
φ
2
∂
x
2
)
=
0
.
{\displaystyle {\mathcal {M}}={\frac {1}{1+\nu }}(M_{11}+M_{22})=D\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)=0\,.}
В этом случае функции
Φ
{\displaystyle \Phi }
Ψ
{\displaystyle \Psi }
Ω
{\displaystyle \Omega }
w
=
w
K
+
M
K
κ
G
h
.
{\displaystyle w=w^{K}+{\frac {{\mathcal {M}}^{K}}{\kappa Gh}}\,.}
Теория Рейсснера-Штейна для консольных пластин[ 23]
q
x
(
y
)
{\displaystyle q_{x}(y)}
x
=
a
{\displaystyle x=a}
b
D
d
4
w
x
d
x
4
=
0
b
3
D
12
d
4
θ
x
d
x
4
−
2
b
D
(
1
−
ν
)
d
2
θ
x
d
x
2
=
0
{\displaystyle {\begin{aligned}&bD{\frac {\mathrm {d} ^{4}w_{x}}{\mathrm {d} x^{4}}}=0\\&{\frac {b^{3}D}{12}}\,{\frac {\mathrm {d} ^{4}\theta _{x}}{\mathrm {d} x^{4}}}-2bD(1-\nu ){\cfrac {d^{2}\theta _{x}}{dx^{2}}}=0\end{aligned}}}
и граничных условиях в точке
x
=
a
{\displaystyle x=a}
b
D
d
3
w
x
d
x
3
+
q
x
1
=
0
,
b
3
D
12
d
3
θ
x
d
x
3
−
2
b
D
(
1
−
ν
)
d
θ
x
d
x
+
q
x
2
=
0
b
D
d
2
w
x
d
x
2
=
0
,
b
3
D
12
d
2
θ
x
d
x
2
=
0
.
{\displaystyle {\begin{aligned}&bD{\cfrac {d^{3}w_{x}}{dx^{3}}}+q_{x1}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{3}\theta _{x}}{dx^{3}}}-2bD(1-\nu ){\cfrac {d\theta _{x}}{dx}}+q_{x2}=0\\&bD{\cfrac {d^{2}w_{x}}{dx^{2}}}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{2}\theta _{x}}{dx^{2}}}=0\,.\end{aligned}}}
Решение этой системы двух ОДУ дает
w
x
(
x
)
=
q
x
1
6
b
D
(
3
a
x
2
−
x
3
)
θ
x
(
x
)
=
q
x
2
2
b
D
(
1
−
ν
)
[
x
−
1
ν
b
(
sinh
(
ν
b
a
)
cosh
[
ν
b
(
x
−
a
)
]
+
tanh
[
ν
b
(
x
−
a
)
]
)
]
{\displaystyle {\begin{aligned}w_{x}(x)&={\frac {q_{x1}}{6bD}}\,(3ax^{2}-x^{3})\\\theta _{x}(x)&={\frac {q_{x2}}{2bD(1-\nu )}}\left[x-{\frac {1}{\nu _{b}}}\,\left({\frac {\sinh(\nu _{b}a)}{\cosh[\nu _{b}(x-a)]}}+\tanh[\nu _{b}(x-a)]\right)\right]\end{aligned}}}
где
ν
b
=
24
(
1
−
ν
)
/
b
{\displaystyle \nu _{b}={\sqrt {24(1-\nu )}}/b}
w
=
w
x
+
y
θ
x
{\displaystyle w=w_{x}+y\theta _{x}}
M
x
x
=
−
D
(
∂
2
w
∂
x
2
+
ν
∂
2
w
∂
y
2
)
=
q
x
1
(
x
−
a
b
)
−
[
3
y
q
x
2
b
3
ν
b
cosh
3
[
ν
b
(
x
−
a
)
]
]
×
[
6
sinh
(
ν
b
a
)
−
sinh
[
ν
b
(
2
x
−
a
)
]
+
sinh
[
ν
b
(
2
x
−
3
a
)
]
+
8
sinh
[
ν
b
(
x
−
a
)
]
]
M
x
y
=
(
1
−
ν
)
D
∂
2
w
∂
x
∂
y
=
q
x
2
2
b
[
1
−
2
+
cosh
[
ν
b
(
x
−
2
a
)
]
−
cosh
[
ν
b
x
]
2
cosh
2
[
ν
b
(
x
−
a
)
]
]
Q
z
x
=
∂
M
x
x
∂
x
−
∂
M
x
y
∂
y
=
q
x
1
b
−
(
3
y
q
x
2
2
b
3
cosh
4
[
ν
b
(
x
−
a
)
]
)
×
[
32
+
cosh
[
ν
b
(
3
x
−
2
a
)
]
−
cosh
[
ν
b
(
3
x
−
4
a
)
]
−
16
cosh
[
2
ν
b
(
x
−
a
)
]
+
23
cosh
[
ν
b
(
x
−
2
a
)
]
−
23
cosh
(
ν
b
x
)
]
.
{\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&=q_{x1}\left({\frac {x-a}{b}}\right)-\left[{\frac {3yq_{x2}}{b^{3}\nu _{b}\cosh ^{3}[\nu _{b}(x-a)]}}\right]\times \\&\quad \left[6\sinh(\nu _{b}a)-\sinh[\nu _{b}(2x-a)]+\sinh[\nu _{b}(2x-3a)]+8\sinh[\nu _{b}(x-a)]\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&={\frac {q_{x2}}{2b}}\left[1-{\frac {2+\cosh[\nu _{b}(x-2a)]-\cosh[\nu _{b}x]}{2\cosh ^{2}[\nu _{b}(x-a)]}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {q_{x1}}{b}}-\left({\frac {3yq_{x2}}{2b^{3}\cosh ^{4}[\nu _{b}(x-a)]}}\right)\times \left[32+\cosh[\nu _{b}(3x-2a)]-\cosh[\nu _{b}(3x-4a)]\right.\\&\qquad \left.-16\cosh[2\nu _{b}(x-a)]+23\cosh[\nu _{b}(x-2a)]-23\cosh(\nu _{b}x)\right]\,.\end{aligned}}}
Напряжения
σ
x
x
=
12
z
h
3
M
x
x
and
σ
z
x
=
1
κ
h
Q
z
x
(
1
−
4
z
2
h
2
)
.
{\displaystyle \sigma _{xx}={\frac {12z}{h^{3}}}\,M_{xx}\quad {\text{and}}\quad \sigma _{zx}={\frac {1}{\kappa h}}\,Q_{zx}\left(1-{\frac {4z^{2}}{h^{2}}}\right)\,.}
Если приложенная нагрузка на краю постоянна, мы восстанавливаем решения для балки при сосредоточенной торцевой нагрузке. Если приложенная нагрузка — линейная функция
y
{\displaystyle y}
q
x
1
=
∫
−
b
/
2
b
/
2
q
0
(
1
2
−
y
b
)
d
y
=
b
q
0
2
;
q
x
2
=
∫
−
b
/
2
b
/
2
y
q
0
(
1
2
−
y
b
)
d
y
=
−
b
2
q
0
12
.
{\displaystyle q_{x1}=\int _{-b/2}^{b/2}q_{0}\left({\frac {1}{2}}-{\frac {y}{b}}\right)\,{\text{d}}y={\frac {bq_{0}}{2}}~;~~q_{x2}=\int _{-b/2}^{b/2}yq_{0}\left({\frac {1}{2}}-{\frac {y}{b}}\right)\,{\text{d}}y=-{\frac {b^{2}q_{0}}{12}}\,.}
↑ Timoshenko et al, 1959 , p. 39.↑ Timoshenko et al, 1959 , p. 82.↑ Reddy, J. N., 2007, Theory and analysis of elastic plates and shells , CRC Press, Taylor and Francis.
↑ Timoshenko, S. and Woinowsky-Krieger, S., (1959), Theory of plates and shells , McGraw-Hill New York.
↑ Timoshenko et al, 1959 , p. 54.↑ Timoshenko et al, 1959 , p. 55.↑ Timoshenko et al, 1959 , p. 56.↑ Timoshenko et al, 1959 , p. 63.↑ Timoshenko et al, 1959 , p. 105.↑ Timoshenko et al, 1959 , p. 106.↑ Cook, R. D. et al., 2002, Concepts and applications of finite element analysis , John Wiley & Sons
↑ 1 2 Timoshenko et al, 1959 , p. 108.↑ 1 2 Timoshenko et al, 1959 , p. 109.↑ Lévy, M., 1899, Comptes rendues , vol. 129, pp. 535—539
↑ Timoshenko et al, 1959 , p. 113.↑ Timoshenko et al, 1959 , p. 114.↑ Timoshenko et al, 1959 , p. 180.↑ Timoshenko et al, 1959 , p. 182.↑ Timoshenko et al, 1959 , p. 184.↑ Timoshenko et al, 1959 , p. 116.↑ Timoshenko et al, 1959 , pp. 180—221.↑ 1 2 Lim, G. T. and Reddy, J. N. О канонических соотношениях для изгиба пластин // International Journal of Solids and Structures. — Т. 40 . — С. 3039—3067 . — doi :10.1016/S0020-7683(03)00084-2 . Архивировано 29 октября 2020 года.↑ E. Reissner and M. Stein. Torsion and transverse bending of cantilever plates // National Advisory Committee for Aeronautics, Technical Note. — 1951. — Т. 2369 . — С. — . Архивировано 29 октября 2020 года.
.



































![{\displaystyle {\cfrac {\partial ^{4}F}{\partial x^{4}}}+2{\cfrac {\partial ^{4}F}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}F}{\partial y^{4}}}=E\left[\left({\cfrac {\partial ^{2}w}{\partial x\partial y}}\right)^{2}-{\cfrac {\partial ^{2}w}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7682816097ae16a8aaf28daa900094b10cf6224e)







![{\displaystyle {\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8083e6e16a9118c0afe8bd3c7e1fe841e17334)














![{\displaystyle \sigma _{rr}={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{rr}+\nu \varepsilon _{\theta \theta }\right]~;~~\sigma _{\theta \theta }={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{\theta \theta }+\nu \varepsilon _{rr}\right]~;~~\sigma _{r\theta }=0\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3113afbe187db314e19db5772f1fb7ec65d5f2bf)

![{\displaystyle D=2Eh^{3}/[3(1-\nu ^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a71aa263a9aeffc5de8a3eeb37a569a193d2443)
![{\displaystyle {\begin{aligned}\sigma _{rr}&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]\\\sigma _{\theta \theta }&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]\\\sigma _{r\theta }&=0\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e9eae0c15eb3c3606cfcbfadf7e523df1069eae)
![{\displaystyle M_{rr}=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]~;~~M_{\theta \theta }=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]~;~~M_{r\theta }=0\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa27857c8e8ae81af9dc56fa29a74b33bc3dad8)























































![{\displaystyle \sum _{m=1}^{\infty }\left[\left({\frac {m\pi }{a}}\right)^{4}Y_{m}\sin {\frac {m\pi x}{a}}-2\left({\frac {m\pi }{a}}\right)^{2}{\cfrac {d^{2}Y_{m}}{dy^{2}}}\sin {\frac {m\pi x}{a}}+{\frac {d^{4}Y_{m}}{dy^{4}}}\sin {\frac {m\pi x}{a}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b7bc6c19d495de8e6086dc8866cf7571b323f9)



![{\displaystyle w(x,y)=\sum _{m=1}^{\infty }\left[\left(A_{m}+B_{m}{\frac {m\pi y}{a}}\right)\cosh {\frac {m\pi y}{a}}+\left(C_{m}+D_{m}{\frac {m\pi y}{a}}\right)\sinh {\frac {m\pi y}{a}}\right]\sin {\frac {m\pi x}{a}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f35b38c6ddc1b29b74377203666d669c5791b2cc)














![{\displaystyle {\begin{aligned}&w(x,y)={\frac {2M_{0}a^{2}}{\pi ^{3}D}}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)^{3}\cosh \alpha _{m}}}\sin {\frac {(2m-1)\pi x}{a}}\times \\&~~\left[\alpha _{m}\,\tanh \alpha _{m}\cosh {\frac {(2m-1)\pi y}{a}}-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05bb4b518f750d8e1aafd47fb079065c5c4a5786)

![{\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&={\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\sin {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.\left\{{\frac {2\nu }{1-\nu }}+\alpha _{m}\tanh \alpha _{m}\right\}\cosh {\frac {(2m-1)\pi y}{a}}\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&=-{\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[{\frac {(2m-1)\pi y}{a}}\cosh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.(1-\alpha _{m}\tanh \alpha _{m})\sinh {\frac {(2m-1)\pi y}{a}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {4M_{0}}{a}}\sum _{m=1}^{\infty }{\frac {1}{\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\cosh {\frac {(2m-1)\pi y}{a}}\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b46371a14545a06c6bb677179132a02137a8fbb4)






![{\displaystyle D=Eh^{3}/[12(1-\nu ^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f3bf995e9bb0214179b93d14f38e7e01cf3a671)
![{\displaystyle c^{2}=2\kappa Gh/[D(1-\nu )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bc4c3ed836ac15ba7c94c0e0fc3cd9fb1d8825a)

![{\displaystyle {\mathcal {M}}=D\left[{\mathcal {A}}\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)-(1-{\mathcal {A}})\nabla ^{2}w\right]+{\frac {2q}{1-\nu ^{2}}}{\mathcal {B}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c93657927f897412a7df1207325d3a731bfa9fed)




















![{\displaystyle {\begin{aligned}w_{x}(x)&={\frac {q_{x1}}{6bD}}\,(3ax^{2}-x^{3})\\\theta _{x}(x)&={\frac {q_{x2}}{2bD(1-\nu )}}\left[x-{\frac {1}{\nu _{b}}}\,\left({\frac {\sinh(\nu _{b}a)}{\cosh[\nu _{b}(x-a)]}}+\tanh[\nu _{b}(x-a)]\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a9eebb0810de812da44e1e62453b7af0aa8dddf)


![{\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&=q_{x1}\left({\frac {x-a}{b}}\right)-\left[{\frac {3yq_{x2}}{b^{3}\nu _{b}\cosh ^{3}[\nu _{b}(x-a)]}}\right]\times \\&\quad \left[6\sinh(\nu _{b}a)-\sinh[\nu _{b}(2x-a)]+\sinh[\nu _{b}(2x-3a)]+8\sinh[\nu _{b}(x-a)]\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&={\frac {q_{x2}}{2b}}\left[1-{\frac {2+\cosh[\nu _{b}(x-2a)]-\cosh[\nu _{b}x]}{2\cosh ^{2}[\nu _{b}(x-a)]}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {q_{x1}}{b}}-\left({\frac {3yq_{x2}}{2b^{3}\cosh ^{4}[\nu _{b}(x-a)]}}\right)\times \left[32+\cosh[\nu _{b}(3x-2a)]-\cosh[\nu _{b}(3x-4a)]\right.\\&\qquad \left.-16\cosh[2\nu _{b}(x-a)]+23\cosh[\nu _{b}(x-2a)]-23\cosh(\nu _{b}x)\right]\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23db4b670f6da6f2f18a0e2419ca828fbc73d657)
