Таблица простых кубических графов (MgQlneg hjkvmd] trQncyvtn] ijgskf)

Перечислены связные 3-регулярные (кубические) простые графы с малым числом вершин.

Связность

Число простых кубических графов с числом вершин 4, 6, 8, 10,… равно 1, 2, 5, 19,…^[1]. Классификация по 1- и 2-связности рёбер сделана, как обычно принято. Остальные кубические графы, вообще говоря, все трёхсвязны, поскольку удаление всех рёбер, смежных какой-либо вершине, приведёт к потере связности. Если использовать определение в свете алгебры взаимодействия моментов импульса^[англ.] (смотрите ниже), дополнительное подразделение 3-связных графов может быть полезным. Выделим следующие подклассы

Нетривиально 3-связные графы могут быть разделены путём удаления 3 рёбер на два подграфа, каждый из которых содержит по меньшей мере две вершины.
Циклически 4-связные — все оставшиеся, то есть не 1-связные, не 2-связные и не тривиально 3-связные.

В таблице эти два случая обозначаются цифрами 3 и 4 в четвёртом столбце.

Рисунок

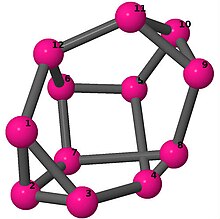
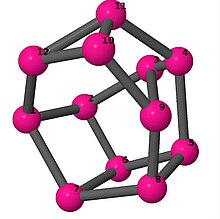
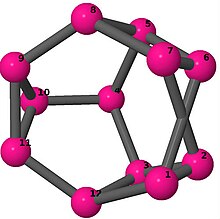
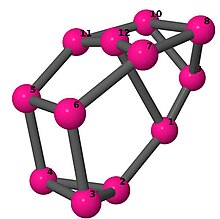
Модели из шаров и стержней показывают граф в стиле изображений молекулярных связей. Комментарии к индивидуальным рисункам содержат обхват, диаметр, индекс Винера, индекс Эстрады^[англ.] и индекс Кирхгофа^[англ.]. Гамильтонов цикл (где существует) показан путём нумерации вершин, начиная с 1. (Положение вершин определено, исходя из евклидова и расстояния из теории графов, которые помещены в MDL Molfile^[англ.], а затем обработаны программой Jmol.)

LCF-нотация

LCF-нотация — система обозначений, разработанная Ледербергом, Коксетером и Фрухтом для представления кубических графов, являющихся гамильтоновыми.

Рёбра цикла в нотацию не включаются. Поскольку граф кубический, в каждой вершине имеется смежное ребро, не принадлежащее циклу. Эти рёбра можно описать, указав, на сколько вершин удалена вторая вершина от первой (со знаком плюс по часовой стрелке и со знаком минус против часовой стрелки). Часто такое представление даёт повторяющиеся последовательности, в этом случае выписывают только такую последовательность, а количество последовательностей показывают индексом.

Пусть v — вершины графа, и v₀v₁,v₁v₂, ... ,v_p-2v_p-1,v_p-1v₀ — гамильтонов цикл из p вершин. Если фиксировать вершину v_i, существует единственная вершина v_j на расстоянии d_i, связанная хордой с v_i,

j=i+d_{i}\quad ({\bmod {\,}}p),\quad 2\leq d_{i}\leq p-2.

Вектор [d₀,d₁, ..., d_p-1] из p целых является удобным, хотя и не единственным, представлением гамильтонова кубического графа. Применяются два дополнительных правила:

Если элемент d_i >p/2, заменяем его на d_i-p;
Избегаем повторения последовательности d_i, если она периодична, и заменяем повторение степенью.

Поскольку начальная вершина пути несущественна, числа в представлении можно циклически сдвигать. Если граф содержит различные гамильтоновы циклы, можно выбрать один из них для LCF-нотации. Один и тот же граф может иметь различные LCF-нотации, в зависимости от того, каким образом были выстроены вершины.

Часто антипалидромическое представление

d_{p-1-i}=-d_{i}\quad ({\bmod {\,}}p),\quad i=0,1,\ldots p/2-1

предпочтительно (если таковое существует), и в этом случае вторая часть заменяется на «;-». LCF-нотация [5,-9,7,-7,9,-5]⁴, например, может быть сокращена до [5,-9,7;-]⁴.

Таблица

4 вершины

диаметр	обхват	Авт^[2]	связность	LCF	название^[англ.]	рисунок
1	3	24	4	[2] ⁴	$K_{4}$	4 вершины, 6 рёбер. Граф Ютсиса ^[3] с 6-j символом

6 вершин

диаметр	обхват	Авт^[2]	связность	LCF	название^[англ.]	рисунок
2	3	12	3	[2,3,-2]²	$W_{n,2}$ , граф призмы $Y_{3}$	6 вершин и 9 рёбер
2	4	72	4	[3]⁶	$K_{3,3}$	6 вершин и 9 рёбер. Граф Ютсиса с 9-j символом^[англ.]

8 вершин

диаметр	обхват	Авт^[2]	связность	LCF	название^[англ.]	рисунок
3	3	16	2	[2,2,-2,-2]²		8 вершин и 12 рёбер
3	3	4	3	[4,-2,4,2]² или [2,3,-2,3;-]		8 вершин и 12 рёбер
2	3	12	3	[2,4,-2,3,3,4,-3,-3]		8 вершин и 12 рёбер
3	4	48	4	[-3,-1,-1,-1,1,1,1,3]	граф куба	8 вершин и 12 рёбер. Граф Ютсиса с 12j-символом второго рода
2	4	16	4	[4] ⁸ или [4,-3,3,4]²	Граф Вагнера	8 вершин и 12 рёбер. Граф Ютсиса с 12j- символом второго рода

10 вершин

диаметр	обхват	Авт^[2]	связность	LCF	название^[англ.]	рисунок
5	3	32	1		Список рёбер list 0-1,0-6,0-9,1-2,1-5,2-3,2-4,3-4, 3-5,4-5,6-7,6-8,7-8,7-9,8-9	10 вершин и 15 рёбер
4	3	4	2	[4,2,3,-2,-4,-3,2,2,-2,-2]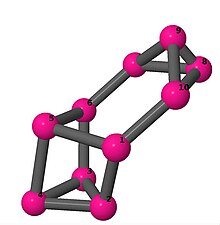
3	3	8	2	[2,-3,-2,2,2;-]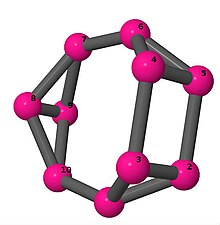
3	3	16	2	[-2,-2,3,3,3;-]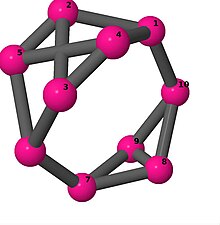
4	3	16	2	[2,2,-2,-2,5] ²
3	3	2	3	[2,3,-2,5,-3] ² [3,-2,4,-3,4,2,-4,-2,-4,2]
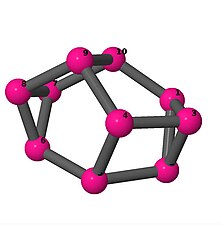3	3	12	3	[2,-4,-2,5,2,4,-2,4,5,-4]		10 вершин и 15 рёбер
3	3	2	3	[5,3,5,-4,-3,5,2,5,-2,4] [-4,2,5,-2,4,4,4,5,-4,-4] [-3,2,4,-2,4,4,-4,3,-4,-4]		10 вершин и 15 рёбер
3	3	4	3	[-4,3,3,5,-3,-3,4,2,5,-2] [3,-4,-3,-3,2,3,-2,4,-3,3]
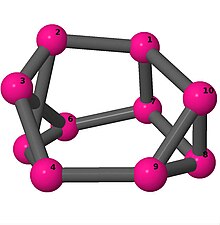3	3	6	3	[3,-3,5,-3,2,4,-2,5,3,-4]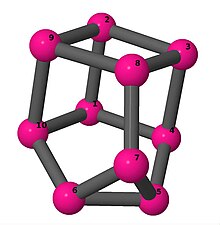
3	3	4	3	[2,3,-2,3,-3;-] [-4,4,2,5,-2]²
3	3	6	3	[5,-2,2,4,-2,5,2,-4,-2,2]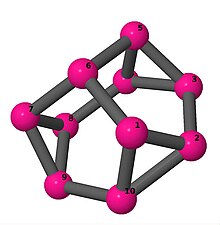
3	3	8	3	[2,5,-2,5,5]² [2,4,-2,3,4;-]		10 вершин и 15 рёбер
3	4	48	3	[5,-3,-3,3,3]²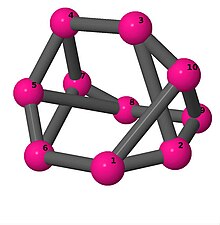
3	4	8	4	[5,-4,4,-4,4]² [5,-4,-3,3,4,5,-3,4,-4,3]		Граф Ютсиса с 15j-символом третьего рода
3	4	4	4	[5,-4,4,5,5]² [-3,4,-3,3,4;-] [4,-3,4,4,-4;-] [-4,3,5,5,-3,4,4,5,5,-4]		Граф Ютсиса с 15j-символом третьего рода
3	4	20	4	[5]¹⁰ [-3,3]⁵ [5,5,-3,5,3]²		Граф Ютсиса с 15j-символом первого рода
3	4	20	4	[-4,4,-3,5,3]²	$G_{5,2}$	Граф Ютсиса с 15j-sсимволом второго рода
2	5	120	4		Граф Петерсена	Граф Ютсиса с 15j-символом пятого рода

12 вершин

диаметр	обхват	Авт^[2]	связность	LCF	название^[англ.]	рисунок
6	3	16	1		Список рёбер 0-1,0-2,0-11,1-2,1-6, 2-3,3-4,3-5,4-5,4-6, 5-6,7-8,7-9,7-11,8-9, 8-10,9-10,10-11
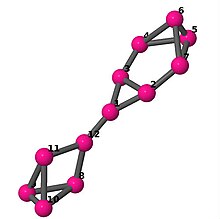5	3	16	1		Список рёбер 0-1,0-6,0-11,1-2,1-3, 2-3,2-5,3-4,4-5,4-6, 5-6,7-8,7-9,7-11, 8-9,8-10,9-10,10-11
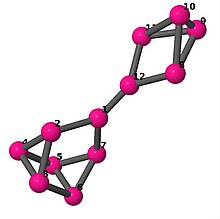6	3	8	1		Список рёбер 0-1,0-3,0-11,1-2,1-6, 2-3,2-5,3-4,4-5,4-6, 5-6,7-8,7-9,7-11,8-9, 8-10,9-10,10-11
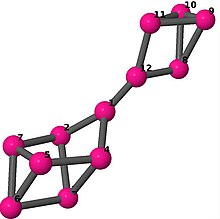5	3	32	1		Список рёбер 0-1,0-6,0-11,1-2,1-4, 2-3,2-5,3-4,3-6,4-5, 5-6,7-8,7-9,7-11,8-9, 8-10,9-10,10-11
5	3	4	2	[3,-2,-4,-3,4,2]² [4,2,3,-2,-4,-3;-]
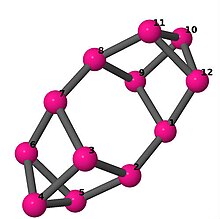4	3	8	2	[3,-2,-4,-3,3,3,3,-3,-3,-3,4,2]
4	3	4	2	[4,2,3,-2,-4,-3,2,3,-2,2,-3,-2]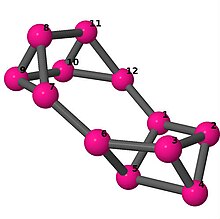
4	4	64	2	[3,3,3,-3,-3,-3]²
4	3	16	2	[2,-3,-2,3,3,3;-]
4	3	16	2	[2,3,-2,2,-3,-2]²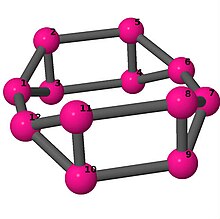
4	3	2	2	[-2,3,6,3,-3,2,-3,-2,6,2,2,-2] [4,2,-4,-2,-4,6,2,2,-2,-2,4,6]
4	3	8	2	[6,3,3,4,-3,-3,6,-4,2,2,-2,-2]
5	3	4	2	[4,2,3,-2,-4,-3,5,2,2,-2,-2,-5]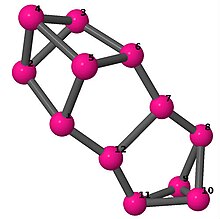
4	3	16	2	[-3,-3,-3,5,2,2;-]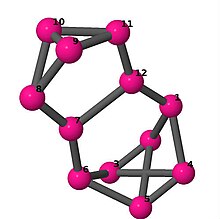
4	3	8	2	[2,-3,-2,5,2,2;-]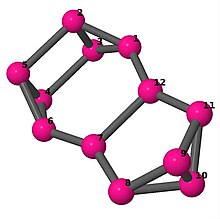
4	3	4	2	[2,4,-2,3,-5,-4,-3,2,2,-2,-2,5] [5,2,-4,-2,-5,-5,2,2,-2,-2,4,5]
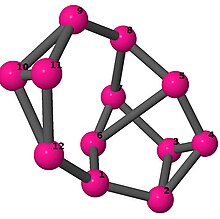4	3	4	2	[-2,-2,4,4,4,4;-] [3,-4,-4,-3,2,2;-] [5,3,4,4,-3,-5,-4,-4,2,2,-2,-2]
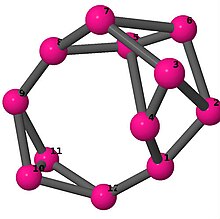4	3	2	2	[4,-2,4,2,-4,-2,-4,2,2,-2,-2,2] [5,-2,2,3,-2,-5,-3,2,2,-2,-2,2]
5	3	16	2	[2,2,-2,-2,-5,5]²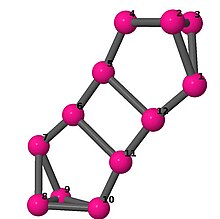
4	3	8	2	[-2,-2,4,5,3,4;-]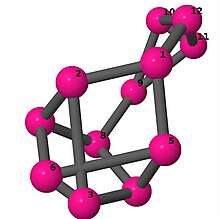
4	3	4	2	[5,2,-3,-2,6,-5,2,2,-2,-2,6,3]
4	3	8	2	[4,-2,3,3,-4,-3,-3,2,2,-2,-2,2]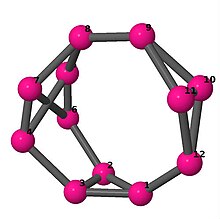
4	3	8	2	[-2,-2,5,3,5,3;-] [-2,-2,3,5,3,-3;-]
5	3	32	2	[2,2,-2,-2,6,6]²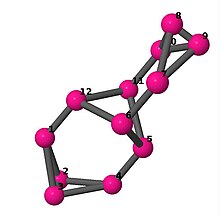
4	3	8	2	[-3,2,-3,-2,2,2;-]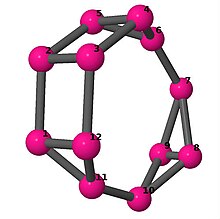
4	3	8	2	[-2,-2,5,2,5,-2;-]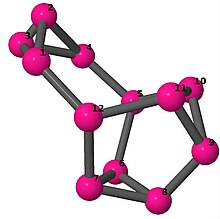
4	3	8	2	[6,-2,2,2,-2,-2,6,2,2,-2,-2,2]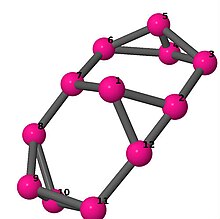
4	3	48	2	[-2,-2,2,2]³
4	3	4	3	[2,3,-2,3,-3,3;-] [-4,6,4,2,6,-2]²
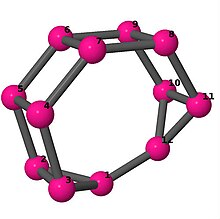4	3	4	3	[-4,6,3,3,6,-3,-3,6,4,2,6,-2] [-2,3,-3,4,-3,3,3,-4,-3,-3,2,3]
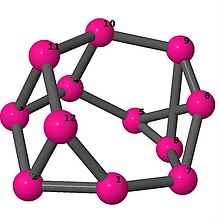4	3	1	3	[-5,2,-3,-2,6,4,2,5,-2,-4,6,3] [-2,3,-3,4,-3,4,2,-4,-2,-4,2,3] [3,-2,3,-3,5,-3,2,3,-2,-5,-3,2]
3	3	4	3	[-5,-5,4,2,6,-2,-4,5,5,2,6,-2] [4,-2,3,4,-4,-3,3,-4,2,-3,-2,2]
3	3	8	3	[-5,-5,3,3,6,-3,-3,5,5,2,6,-2] [2,4,-2,3,5,-4,-3,3,3,-5,-3,-3]
4	3	2	3	[2,4,-2,3,6,-4,-3,2,3,-2,6,-3] [2,4,-2,3,5,-4,-3,4,2,-5,-2,-4] [-5,2,-3,-2,5,5,2,5,-2,-5,-5,3]
4	3	2	3	[-5,2,-3,-2,6,3,3,5,-3,-3,6,3] [4,-2,-4,4,-4,3,3,-4,-3,-3,4,2] [-3,3,3,4,-3,-3,5,-4,2,3,-2,-5]
4	3	2	3	[2,3,-2,4,-3,6,3,-4,2,-3,-2,6] [-4,5,-4,2,3,-2,-5,-3,4,2,4,-2]
4	3	1	3	[6,3,-4,-4,-3,3,6,2,-3,-2,4,4] [-5,-4,4,2,6,-2,-4,5,3,4,6,-3] [3,4,4,-3,4,-4,-4,3,-4,2,-3,-2] [4,5,-4,-4,-4,3,-5,2,-3,-2,4,4] [4,5,-3,-5,-4,3,-5,2,-3,-2,5,3]
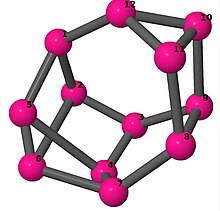3	4	4	3	[4,6,-4,-4,-4,3,3,6,-3,-3,4,4] [-5,-4,3,3,6,-3,-3,5,3,4,6,-3] [4,-3,5,-4,-4,3,3,-5,-3,-3,3,4]
3	4	16	3	[3,3,4,-3,-3,4;-] [3,6,-3,-3,6,3]²
4	3	1	3	[4,-2,5,2,-4,-2,3,-5,2,-3,-2,2] [5,-2,2,4,-2,-5,3,-4,2,-3,-2,2] [2,-5,-2,-4,2,5,-2,2,5,-2,-5,4]	Граф Фрухта
4	3	4	3	[-2,6,2,-4,-2,3,3,6,-3,-3,2,4] [-2,2,5,-2,-5,3,3,-5,-3,-3,2,5]
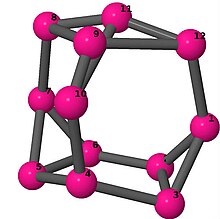4	3	2	3	[2,4,-2,6,2,-4,-2,4,2,6,-2,-4] [2,5,-2,2,6,-2,-5,2,3,-2,6,-3]
4	3	2	3	[6,3,-3,-5,-3,3,6,2,-3,-2,5,3] [3,5,3,-3,4,-3,-5,3,-4,2,-3,-2] [-5,-3,4,2,5,-2,-4,5,3,-5,3,-3]
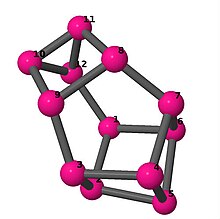4	4	12	3	[3,-3,5,-3,-5,3,3,-5,-3,-3,3,5]
4	3	2	3	[4,2,4,-2,-4,4;-] [3,5,2,-3,-2,5;-] [6,2,-3,-2,6,3]²
4	3	2	3	[3,6,4,-3,6,3,-4,6,-3,2,6,-2] [4,-4,5,3,-4,6,-3,-5,2,4,-2,6] [-5,5,3,-5,4,-3,-5,5,-4,2,5,-2]
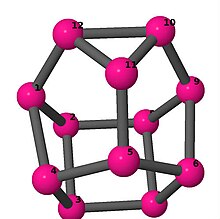3	3	1	3	[6,-5,2,6,-2,6,6,3,5,6,-3,6] [6,2,-5,-2,4,6,6,3,-4,5,-3,6] [5,5,6,4,6,-5,-5,-4,6,2,6,-2] [-4,4,-3,3,6,-4,-3,2,4,-2,6,3] [6,2,-4,-2,4,4,6,4,-4,-4,4,-4] [-3,2,5,-2,-5,3,4,-5,-3,3,-4,5] [-5,2,-4,-2,4,4,5,5,-4,-4,4,-5]
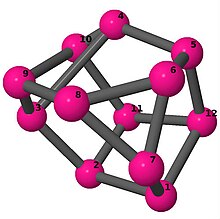3	3	2	3	[2,6,-2,5,6,4,5,6,-5,-4,6,-5] [5,6,-4,-4,5,-5,2,6,-2,-5,4,4] [2,4,-2,-5,4,-4,3,4,-4,-3,5,-4] [2,-5,-2,4,-5,4,4,-4,5,-4,-4,5]
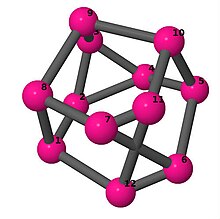4	3	4	3	[2,4,-2,-5,5]² [-5,2,4,-2,6,3,-4,5,-3,2,6,-2]
4	3	2	3	[-4,-4,4,2,6,-2,-4,4,4,4,6,-4] [-4,-3,4,2,5,-2,-4,4,4,-5,3,-4] [-3,5,3,4,-5,-3,-5,-4,2,3,-2,5]
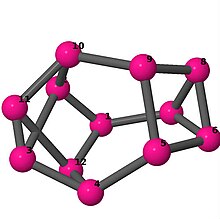3	3	2	3	[2,5,-2,4,4,5;-] [2,4,-2,4,4,-4;-] [-5,5,6,2,6,-2] ² [5,-2,4,6,3,-5,-4,-3,2,6,-2,2]
3	3	2	3	[3,6,-4,-3,5,6,2,6,-2,-5,4,6] [2,-5,-2,4,5,6,4,-4,5,-5,-4,6] [5,-4,4,-4,3,-5,-4,-3,2,4,-2,4]
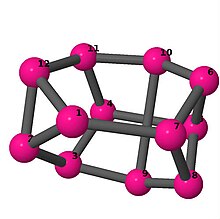4	3	2	3	[6,-5,2,4,-2,5,6,-4,5,2,-5,-2] [-2,4,5,6,-5,-4,2,-5,-2,6,2,5] [5,-2,4,-5,4,-5,-4,2,-4,-2,5,2]
4	3	1	3	[2,-5,-2,6,3,6,4,-3,5,6,-4,6] [6,3,-3,4,-3,4,6,-4,2,-4,-2,3] [5,-4,6,-4,2,-5,-2,3,6,4,-3,4] [5,-3,5,6,2,-5,-2,-5,3,6,3,-3] [-5,2,-5,-2,6,3,5,5,-3,5,6,-5] [-3,4,5,-5,-5,-4,2,-5,-2,3,5,5] [5,5,5,-5,4,-5,-5,-5,-4,2,5,-2]
3	3	2	3	[5,-3,6,3,-5,-5,-3,2,6,-2,3,5] [2,6,-2,-5,5,3,5,6,-3,-5,5,-5] [5,5,5,6,-5,-5,-5,-5,2,6,-2,5] [4,-3,5,2,-4,-2,3,-5,3,-3,3,-3] [5,5,-3,-5,4,-5,-5,2,-4,-2,5,3]
4	3	4	3	[2,4,-2,5,3,-4;-] [5,-3,2,5,-2,-5;-] [3,6,3,-3,6,-3,2,6,-2,2,6,-2]
4	3	2	3	[6,2,-4,-2,-5,3,6,2,-3,-2,4,5] [2,3,-2,4,-3,4,5,-4,2,-4,-2,-5] [-5,2,-4,-2,-5,4,2,5,-2,-4,4,5]
3	3	2	3	[5,2,5,-2,5,-5;-] [6,2,-4,-2,4,6]² [2,-5,-2,6,2,6,-2,3,5,6,-3,6] [-5,-2,6,6,2,5,-2,5,6,6,-5,2]
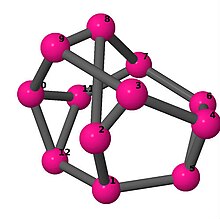3	3	12	3	[-5,3,3,5,-3,-3,4,5,-5,2,-4,-2]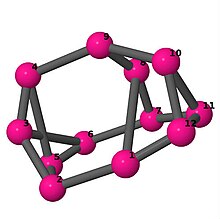
3	3	2	3	[6,-4,3,4,-5,-3,6,-4,2,4,-2,5] [-4,6,-4,2,5,-2,5,6,4,-5,4,-5] [5,-5,4,-5,3,-5,-4,-3,5,2,5,-2]
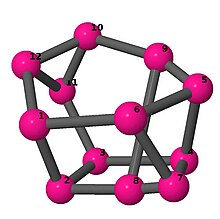4	3	12	3	[-4,5,2,-4,-2,5;-]	Граф Дюрера
3	3	4	3	[2,5,-2,5,3,5;-] [6,-2,6,6,6,2]² [5,-2,6,6,2,-5,-2,3,6,6,-3,2]
3	3	4	3	[6,-2,6,4,6,4,6,-4,6,-4,6,2] [5,6,-3,3,5,-5,-3,6,2,-5,-2,3]
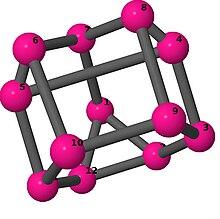3	3	4	3	[4,-2,4,6,-4,2,-4,-2,2,6,-2,2] [5,-2,5,6,2,-5,-2,-5,2,6,-2,2]
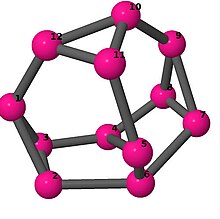3	3	24	3	[6,-2,2]⁴	Усечённый тетраэдр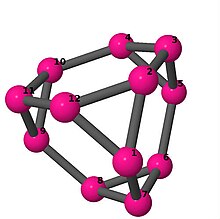
3	3	12	3		Граф Титце
3	3	36	3	[2,6,-2,6] ³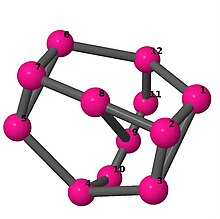
4	4	24	4	[-3,3]⁶ [3,-5,5,-3,-5,5] ²	$G_{6,2}$ , $Y_{6}$	Граф Ютсиса, 18j-символ, метка: B
3	4	4	4	[6,-3,6,6,3,6]² [6,6,-5,5,6,6]² [3,-3,4,-3,3,4;-] [5,-3,6,6,3,-5]² [5,-3,-5,4,4,-5;-] [6,6,-3,-5,4,4,6,6,-4,-4,5,3]		Граф Ютсиса, 18j-символ, метка: L
3	4	8	4	[-4,4,4,6,6,-4]² [6,-5,5,-5,5,6]² [4,-3,3,5,-4,-3;-] [-4,-4,4,4,-5,5]²		Граф Ютсиса, 18j-символ, метка: K
3	4	2	4	[-4,6,3,6,6,-3,5,6,4,6,6,-5] [-5,4,6,6,6,-4,5,5,6,6,6,-5] [5,-3,4,6,3,-5,-4,-3,3,6,3,-3] [4,-4,6,4,-4,5,5,-4,6,4,-5,-5] [4,-5,-3,4,-4,5,3,-4,5,-3,-5,3]		Граф Ютсиса, 18j-символ, метка: T
3	4	2	4	[3,4,5,-3,5,-4;-] [3,6,-4,-3,4,6]² [-4,5,5,-4,5,5;-] [3,6,-4,-3,4,4,5,6,-4,-4,4,-5] [4,-5,5,6,-4,5,5,-5,5,6,-5,-5] [4,-4,5,-4,-4,3,4,-5,-3,4,-4,4]		Граф Ютсиса, 18j-символ, метка: R
3	4	8	4	[4,-4,6]⁴ [3,6,3,-3,6,-3]² [-3,6,4,-4,6,3,-4,6,-3,3,6,4]	Бидиакис-куб	Граф Ютсиса, 18j-символ, метка: D
3	4	16	4	[6,-5,5]⁴ [3,4,-4,-3,4,-4] ²		Граф Ютсиса, 18j-символ, метка: G
3	4	2	4	[-3,5,-3,4,4,5;-] [4,-5,5,6,-4,6]² [-3,4,-3,4,4,-4;-] [5,6,-3,-5,4,-5,3,6,-4,-3,5,3] [5,6,4,-5,5,-5,-4,6,3,-5,5,-3]		Граф Ютсиса, 18j-символ, метка: S
3	4	4	4	[4,-3,4,5,-4,4;-] [4,5,-5,5,-4,5;-] [-5,-3,4,5,-5,4;-]		Граф Ютсиса, 18j-символ, метка: N
3	4	2	4	[6,-4,6,-4,3,5,6,-3,6,4,-5,4] [6,-4,3,-4,4,-3,6,3,-4,4,-3,4] [5,6,-4,3,5,-5,-3,6,3,-5,4,-3] [5,-5,4,6,-5,-5,-4,3,5,6,-3,5] [5,5,-4,4,5,-5,-5,-4,3,-5,4,-3]		Граф Ютсиса, 18j-символ, метка: V
3	4	4	4	[6,-3,5,6,-5,3,6,-5,-3,6,3,5] [3,-4,5,-3,4,6,4,-5,-4,4,-4,6]		Граф Ютсиса, 18j-символ, метка: P
3	4	8	4	[5,6,6,-4,5,-5,4,6,6,-5,-4,4]		Граф Ютсиса, 18j-символ, метка: I
3	5	16	4	[4,-5,4,-5,-4,4;-]		Граф Ютсиса, 18j-символ, метка: F
3	4	4	4	[6,4,6,6,6,-4]² [-3,4,-3,5,3,-4;-] [-5,3,6,6,-3,5,5,5,6,6,-5,-5] [-3,3,6,4,-3,5,5,-4,6,3,-5,-5]		Граф Ютсиса, 18j-символ, метка: M
4	4	8	4	[3,5,5,-3,5,5;-] [-3,5,-3,5,3,5;-] [5,-3,5,5,5,-5;-]		Граф Ютсиса, 18j-символ, метка: E
3	4	48	4	[5,-5,-3,3]³ [-5,5]⁶	Граф Франклина	Граф Ютсиса, 18j-символ, метка: C
3	4	24	4	[6]¹² [6,6,-3,-5,5,3]²		Граф Ютсиса, 18j-символ, метка: A
3	5	18	4	[6,-5,-4,4,-5,4,6,-4,5,-4,4,5]		Граф Ютсиса, 18j-символ, метка: H

Колонка LCF пуста, если у графа нет гамильтонова цикла, что наблюдается довольно редко (гипотеза Тэйта). В этом случае список рёбер между парами вершин с индексами от 0 до n-1 в третьем столбце используется как идентификатор.

Вектор коэффициентов взаимодействия

Каждый 4-связный (в выше определённом смысле) простой кубический граф с 2n вершинами определяет класс квантовой механики 3n-j символов. Грубо говоря, каждая вершина представляет 3jm-символ, граф превращается в орграф путём назначения знаков моментам инерции квантовых чисел j, вершины помечаются согласно направленности в дереве j (дерево вершин) 3-jm символов, а граф представляет сумму произведений всех этих чисел, присвоенных вершинам.

Имеется 1 (6j), 1 (9j^[англ.]), 2 (12j), 5 (15j), 18 (18j), 84 (21j), 607 (24j), 6100 (27j), 78824 (30j), 1195280 (33j), 20297600 (36j), 376940415 (39j) и т. д. таких символов^[4].

Если они эквивалентны некоторому порождённому вершинами бинарному дереву (вырезается одно ребро и находится сечение, которое разрезает граф на два дерева), они представляют коэффициенты вторичного взаимодействия, и тоже известны как графы Ютсиса^[5].

Примечания

↑ последовательность A002851 в OEIS
↑ ¹ ² ³ ⁴ ⁵ Автоморфизмов
↑ Графы Ютсиса (Yutsis graphs) — это связные простые графы, которые можно разложить на два порождённых вершинами дерева. Назван по имени Адальфа Ютсиса (Adolfas Jucys). (Van Dyck, Brinkmann, Fack, McKay 2005) (Aldred, Van Dyck, Brinkmann, Fack, McKay 2009)
↑ последовательность A175847 в OEIS
↑ последовательность A111916 в OEIS

Ссылки

A. P. Yutsis, I. B. Levinson, V. V. Vanagas, A. Sen. Mathematical Apparatus of the theory of angular momentum. — Israel program for scientific translations, 1962.
J.-N. Massot, E. El-Baz, J. Lafoucriere. A general graphical method for angular momentum // Reviews of Modern Physics. — 1967. — Т. 39, вып. 2. — С. 288–305. — doi:10.1103/RevModPhys.39.288.
F. C. Bussemaker, S. Cobeljic, D. M. Cvetkovic. Computer investigations of cubic graphs. — 1976.
F. C. Bussemaker, S. Cobeljic, D. M. Cvetkovic, J. J. Seidel. Cubic graphs on <=14 vertices // J. Combin. Theory B. — 1977. — Т. 23. — С. 234–235. — doi:10.1016/0095-8956(77)90034-X.
R. Frucht. A canonical representation of trivalent Hamiltonian graphs // Journal of Graph Theory. — 1977. — Т. 1, вып. 1. — С. 45–60. — doi:10.1002/jgt.3190010111.
L. Clark, R. Entringer. Smallest maximally non-Hamiltonian graphs // Per. Mathem. Hungar.. — 1983. — Т. 14, вып. 1. — С. 57–68. — doi:10.1007/BF02023582.
N. C. Wormald. Enumeration of cyclically 4-connected cubic graphs // Journal of Graph Theory. — 1985. — Т. 9. — С. 563–573. — doi:10.1002/jgt.3190090418.
A. Bar-Shalom, M. Klapisch. NJGRAF - an efficient program for calculation of general recoupling coefficients by graphical analysis, compatible with NJSYM // Comp. Phys. Comm.. — 1988. — Т. 50, вып. 3. — С. 375–393. — doi:10.1016/0010-4655(88)90192-0.
G. Brinkmann. Fast generation of cubic graphs // Journal of Graph Theory. — 1996. — Т. 23, вып. 2. — С. 139–149. — doi:10.1002/(SICI)1097-0118(199610)23:2<139::AID-JGT5>3.0.CO;2-U.
V. Fack, S. N. Pitre, J. Van der Jeugt. Calculation of general recoupling coefficients using graphical methods // Comp. Phys. Comm.. — 1997. — Т. 101, вып. 1–2. — С. 155–170. — doi:10.1016/S0010-4655(96)00170-1.
M. Danos, U. Fano. Graphical analysis of angular momentum for collision products // Physics Reports. — 1998. — Т. 304, вып. 4. — С. 155–227. — doi:10.1016/S0370-1573(98)00020-9.
M. Meringer. Fast generation of regular graphs and construction of cages // Journal of Graph Theory. — 1999. — Т. 30, вып. 2. — С. 137–146. — doi:10.1002/(SICI)1097-0118(199902)30:2<137::AID-JGT7>3.0.CO;2-G.
D. Van Dyck, G. Brinkmann, V. Fack, B. D. McKay. To be or not to be Yutsis: Algorithms for the decision problem // Comp. Phys. Comm.. — 2005. — Т. 173, вып. 1–2. — С. 61–70. — doi:10.1016/j.cpc.2005.07.008.
D. Van Dyck, V. Fack. On the reduction of Yutsis graphs // Disc. Math.. — 2007. — Т. 307, вып. 11–12. — С. 1506–1515. — doi:10.1016/j.disc.2005.11.088.
R. E. L. Aldred, D. Van Dyck, G. Brinkmann, V. Fack, B. D. McKay. Graph structural properties of non- Yutsis graphs allowing fast recognition // Disc. Math.. — 2009. — Т. 157, вып. 2. — С. 377–386. — doi:10.1016/j.dam.2008.03.020.

[1] последовательность A002851 в OEIS

[aut-2] ¹ ² ³ ⁴ ⁵ Автоморфизмов

[3] Графы Ютсиса (Yutsis graphs) — это связные простые графы, которые можно разложить на два порождённых вершинами дерева. Назван по имени Адальфа Ютсиса (Adolfas Jucys). (Van Dyck, Brinkmann, Fack, McKay 2005) (Aldred, Van Dyck, Brinkmann, Fack, McKay 2009)

[4] последовательность A175847 в OEIS

[5] последовательность A111916 в OEIS

[1]

[2]

[3]

[4]

[5]