Эта статья входит в число добротных статей

Предсказание вторичной структуры РНК (Hjy;vtg[guny fmkjncukw vmjrtmrjd JUT)

Перейти к навигации Перейти к поиску

Предсказа́ние втори́чной структу́ры РНК — метод определения вторичной структуры нуклеиновой кислоты по последовательности её нуклеотидов. Вторичную структуру можно предсказывать для единичной последовательности или анализировать множественное выравнивание семейства родственных РНК.

Вторичная структура нуклеиновой кислоты зависит, главным образом, от спаривания оснований друг с другом и стэкинг-взаимодействий. Однако во многих случаях вторичная структура РНК сохраняется в ходе эволюции в большей степени, чем её первичная последовательность[1]. Многие способы предсказания вторичной структуры основаны на методе динамического программирования и не в состоянии эффективно выявлять псевдоузлы.

Несмотря на схожесть, существуют некоторые различия в методах предсказания структур ДНК и РНК. В естественных условиях ДНК чаще всего представляет собой полностью комплементарный дуплекс, в то время как РНК образует сложные вторичные и третичные структуры, как, например, у тРНК, рибосомальных РНК или сплайсосом. Происходит это отчасти потому, что дополнительный атом кислорода в составе рибозы увеличивает склонность к образованию водородной связи основной цепью нуклеиновой кислоты. Отличаются и энергетические параметры двух этих нуклеиновых кислот.

Предсказание структуры единичной молекулы РНК

[править | править код]

Вторичная структура небольших молекул РНК в значительной степени определяется сильными локальными взаимодействиями, такими как водородные связи и стэкинг-взаимодействия пар оснований. Сумма свободных энергий таких взаимодействий должна обеспечивать стабильность данной структуры. Для предсказания свободной энергии укладки вторичной структуры используется модель ближайшего соседа (англ. nearest-neighbor model). В этой модели изменение свободной энергии для каждого мотива зависит от последовательности самого мотива и ближайших к нему пар оснований[2]. Модель и параметры минимальной энергии для классических Уотсон-Криковских пар, пары гуанин-урацил и петли были получены эмпирическими калориметрическими экспериментами, самые современные параметры были опубликованы в 2004 году[3], хотя большинство программных пакетов до сих пор использует предыдущий набор, собранный в 1999 году[4].

Самый простой способ найти структуру с минимальной свободной энергией — это генерировать все возможные структуры и вычислить для них свободную энергию, но число возможных структур последовательности экспоненциально возрастает с увеличением длины РНК (Количество вторичных структур = (1,8) N, где N — число нуклеотидов)[5]. Так, для РНК длиной всего в 200 пар нуклеотидов существует более 1050 возможных структур со спаренными основаниями[1].

Алгоритмы на основе динамического программирования

[править | править код]

Одним из подходов к предсказанию вторичной структуры РНК является алгоритм Нуссинов, основанный на динамическом программировании и заключающийся в нахождении структуры с наибольшим количеством пар оснований[6]. Однако этот алгоритм слишком прост и не учитывает важные структурные свойства, такие как предпочтения определенных длин петель или предпочтения определенных ближайших соседей по структуре, возникающие вследствие стэкинг-взаимодействий между соседними парами оснований в шпильках РНК[1]. Кроме того, решение часто бывает не единственное. В 1980 году Нуссинов с коллегами опубликовали адаптацию их подхода, используя простую энергетическую модель ближайших соседей[7].

Сворачивание РНК обусловлено физическими причинами, а не подсчётом и максимизацией числа спаренных оснований. Метод, предложенный в 1981 году Майклом Цукером и Патриком Стейглером, предполагает, что правильная структура в равновесии обладает наименьшей свободной энергией (ΔG)[8]. ΔG вторичной структуры РНК оценивается как сумма свободных энергий петель, пар оснований и других элементов вторичной структуры. Важное отличие от более простого алгоритма Нуссинов заключается в том, что при вычислении энергии шпилек энергия стэкинга соответствует взаимодействию соседних пар оснований, а не самим парам[1].

Динамическое программирование позволяет проверить все возможные варианты вторичных структур РНК без непосредственного их создания. Алгоритм работает рекурсивно. Наилучшая структура с минимальной возможной энергией рассчитывается сперва для всевозможных маленьких подпоследовательностей, а затем — для всё больших и больших подпоследовательностей. Точное строение молекулы РНК определяется вычислением минимальной свободной энергии полной последовательности[2].

Алгоритмы динамического программирования обычно используются, чтобы обнаружить «хорошо вложенные» паттерны пар оснований, то есть те, которые образуют водородные связи, не перекрывающиеся с другими участками последовательности. К таким структурам относятся двойные спирали, стеблевые петли и варианты «клеверного листа», встречающиеся, например, в транспортной РНК. Эти методы основаны на заданных расчетных параметрах, оценивающих свободную энергию спаривания определенных типов пар оснований, включая Уотсона-Криковские и Хугстиновские пары. В зависимости от сложности метода, одиночные пары оснований могут рассматриваться так же, как и короткие сегменты из двух-трех пар оснований для учёта эффекта стекинг-взаимодействий. Без существенных алгоритмических модификаций, требующих чрезвычайно больших вычислительных затрат, эти методы не могут определить псевдоузлы[9].

Субоптимальные структуры

[править | править код]

Точность предсказания вторичной структуры единичной молекулы РНК путём минимизации свободной энергии ограничивается несколькими факторами:

  1. В модели ближайшего соседа величина свободной энергии не может принимать некоторые допустимые значения.
  2. Не все известные РНК укладки соответствуют термодинамическому минимуму.
  3. Некоторые последовательности РНК имеют более одной биологически активной конформации (так называемые, рибопереключатели)

По этой причине способ предсказания вторичных структур с похожим низким значением свободной энергии может дать существенную информацию. Такие структуры называются субоптимальными. MFOLD — одна из программ, генерирующих субоптимальные структуры[10].

Предсказание псевдоузлов

[править | править код]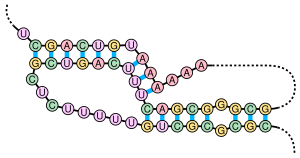
Псевдоузел из РНК-компонента теломеразы[англ.]

Одной из проблем предсказания вторичной структуры РНК является то, что стандартные методы минимизации свободной энергии и статистические методы не могут выявить псевдоузлы[4]. Этот недостаток объясняется тем, что обычные алгоритмы динамического программирования рассматривают только взаимодействия между ближайшими нуклеотидами, в то время как псевдоузлы образуются в результате взаимодействия между удаленными нуклеотидами. Ривас и Эдди опубликовали алгоритм динамического программирования для прогнозирования псевдоузлов[9]. Однако этот алгоритм динамического программирования осуществляется очень медленно. Время работы стандартного алгоритма динамического программирования для минимизации свободной энергии составляет O (N3) (N — число нуклеотидов в последовательности), а алгоритм Риваса и Эдди требует O (N6) по времени. Это побудило исследователей к реализации версии алгоритма, которая ограничивает классы псевдоузлов, позволяя сэкономить время. Например, pknotsRG, включающий в себя только класс простых рекурсивных псевдоузлов, требует O (N4) операций[11].

Другие подходы к предсказанию вторичной структуры РНК

[править | править код]

Другим подходом для предсказания вторичной структуры РНК является определение укладки с помощью ансамбля Больцмана[12][13], например, в программе SFOLD. Данная программа генерирует статистическую выборку всех возможных вторичных структур РНК. Алгоритм отбирает вторичные структуры в соответствии с распределением Больцмана. Подобный метод отбора предлагает хорошее решение проблемы неопределенности в укладке[13].

Предсказание вторичной структуры семейств родственных РНК

[править | править код]

Ковариантные модели основаны на существовании семейств родственных РНК, имеющих не только общую вторичную структуру, но и некоторые общие мотивы в последовательностях. Эти методы анализируют ковариацию отдельных сайтов оснований в ходе эволюции; сохранение двух довольно удаленных друг от друга нуклеотидов указывает на наличие структурно необходимой водородной связи между ними. Было показано, что проблема предсказания псевдоузлов является NP-полной задачей[14]

Проблема выравнивания и предсказания консенсусной структуры тесно связаны. Можно выделить три различных подхода к предсказанию консенсусных структур[15]:

  1. Укладка выравнивания;
  2. Одновременное выравнивание последовательностей и укладка;
  3. Выравнивание предсказанных структур.

Выравнивание с последующей укладкой

[править | править код]

Данный подход заключается в построении множественного выравнивания последовательностей РНК, нахождении консенсусной последовательности, а затем её укладке. Качество выравнивания определяет точность консенсусной структурной модели. Консенсусная последовательность укладывается с использованием различных подходов, таких же, как и для предсказания вторичной структуры единичных молекул РНК. Подход, использующий термодинамическую укладку использует, например, программа RNAalifold[16]. Различные подходы используют программы Pfold и ILM. Программа Pfold реализует стохастические контекстно-свободные грамматики (СКСГ)[17]. ILM (iterated loop matching), в отличие от других алгоритмов укладки выравнивания, может восстанавливать псевдоузлы. Он использует сочетание термодинамики и оценки соответствующего информационного содержания[18].

Синхронное выравнивание и укладка

[править | править код]

Эволюция часто сохраняет функциональную структуру РНК лучше, чем её последовательность[16]. Таким образом, задача заключается в создании общей структуры для двух или более высоко дивергентных, но гомологичных последовательностей РНК. На практике выравнивания последовательностей становятся непригодными и не помогают повысить точность предсказания структуры, когда сходство двух последовательностей составляет менее 50 %[19].

Программы на основе структурных выравниваний повышают производительность этих методов, большинство из которых являются вариантами алгоритма Sankoff[20]. В принципе, алгоритм Sankoff представляет собой объединение алгоритмов выравнивания последовательностей и Nussinov[6], который ищет максимальный участок спаривания с помощью динамического программирования[21]. Алгоритм Sankoff сам по себе является теоретическим, поскольку требует очень больших вычислительных ресурсов (время работы O(n3m) и O(n2m) памяти, где N — длина последовательности, m — число последовательностей). Однако существуют некоторые попытки реализации ограниченных версий алгоритма Sankoff. К ним относятся, например, Foldalign[22][23], Dynalign[24][25], PMmulti/PMcomp[21], Stemloc[26] и Murlet[27]. В этих реализациях ограничены максимальная длина выравнивания или количество возможных вариантов консенсусной структуры. Так, Foldalign строит локальные выравнивания и ограничивает возможную длину выравнивания последовательностей.

Укладка с последующим выравниванием

[править | править код]

Выравнивание предсказанных структур применяется менее широко. Данный подход использует структуры, предсказанные для одиночных молекул РНК. Он выравнивает их с использованием деревьев[28]. Основная слабость такого подхода заключается в том, что предсказания одной последовательности часто неточны, таким образом, нарушается точность всего дальнейшего анализа.

См. также

[править | править код]

Примечания

[править | править код]
  1. ↑ 1 2 3 4 Р. Дурбин, Ш. Эдди, А. Крог, Г. Митчисон. Анализ биологических последовательностей.. — М.-Ижевск.: НИЦ "Регулярная и хаотическая динамика", Институт компьютерных исследований, 2006. — С. 347-402. — 480 с. — ISBN 5-93972-559-7.
  2. ↑ 1 2 Mathews D. H. Revolutions in RNA secondary structure prediction. (англ.) // Journal of molecular biology. — 2006. — Vol. 359, no. 3. — P. 526—532. — doi:10.1016/j.jmb.2006.01.067. — PMID 16500677. [исправить]
  3. ↑ Mathews D. H., Disney M. D., Childs J. L., Schroeder S. J., Zuker M., Turner D. H. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. (англ.) // Proceedings of the National Academy of Sciences of the United States of America. — 2004. — Vol. 101, no. 19. — P. 7287—7292. — doi:10.1073/pnas.0401799101. — PMID 15123812. [исправить]
  4. ↑ 1 2 Mathews D. H., Sabina J., Zuker M., Turner D. H. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. (англ.) // Journal of molecular biology. — 1999. — Vol. 288, no. 5. — P. 911—940. — doi:10.1006/jmbi.1999.2700. — PMID 10329189. [исправить]
  5. ↑ Zuker M., Sankoff D. RNA secondary structures and their prediction (неопр.) // Bull. Math. Biol.. — 1984. — Т. 46. — С. 591—621.
  6. ↑ 1 2 Nussinov R, Piecznik G, Grigg JR and Kleitman DJ. Algorithms for loop matchings // SIAM Journal on Applied Mathematics. — 1978. — Vol. 35, № 1. — P. 68—82. Архивировано 30 марта 2021 года.
  7. ↑ Nussinov R., Jacobson A. B. Fast algorithm for predicting the secondary structure of single-stranded RNA. (англ.) // Proceedings of the National Academy of Sciences of the United States of America. — 1980. — Vol. 77, no. 11. — P. 6309—6313. — PMID 6161375. [исправить]
  8. ↑ Zuker M., Stiegler P. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. (англ.) // Nucleic acids research. — 1981. — Vol. 9, no. 1. — P. 133—148. — PMID 6163133. [исправить]
  9. ↑ 1 2 Rivas E., Eddy S. R. A dynamic programming algorithm for RNA structure prediction including pseudoknots. (англ.) // Journal of molecular biology. — 1999. — Vol. 285, no. 5. — P. 2053—2068. — doi:10.1006/jmbi.1998.2436. — PMID 9925784. [исправить]
  10. ↑ Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. (англ.) // Nucleic acids research. — 2003. — Vol. 31, no. 13. — P. 3406—3415. — PMID 12824337. [исправить]
  11. ↑ Reeder J., Giegerich R. Design, implementation and evaluation of a practical pseudoknot folding algorithm based on thermodynamics. (англ.) // BMC bioinformatics. — 2004. — Vol. 5. — P. 104. — doi:10.1186/1471-2105-5-104. — PMID 15294028. [исправить]
  12. ↑ McCaskill J. S. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. (англ.) // Biopolymers. — 1990. — Vol. 29, no. 6-7. — P. 1105—1119. — doi:10.1002/bip.360290621. — PMID 1695107. [исправить]
  13. ↑ 1 2 Ding Y., Lawrence C. E. A statistical sampling algorithm for RNA secondary structure prediction. (англ.) // Nucleic acids research. — 2003. — Vol. 31, no. 24. — P. 7280—7301. — PMID 14654704. [исправить]
  14. ↑ Lyngsø R. B., Pedersen C. N. RNA pseudoknot prediction in energy-based models. (англ.) // Journal of computational biology : a journal of computational molecular cell biology. — 2000. — Vol. 7, no. 3-4. — P. 409—427. — doi:10.1089/106652700750050862. — PMID 11108471. [исправить]
  15. ↑ Gardner P. P., Giegerich R. A comprehensive comparison of comparative RNA structure prediction approaches. (англ.) // BMC bioinformatics. — 2004. — Vol. 5. — P. 140. — doi:10.1186/1471-2105-5-140. — PMID 15458580. [исправить]
  16. ↑ 1 2 Hofacker I. L., Fekete M., Stadler P. F. Secondary structure prediction for aligned RNA sequences. (англ.) // Journal of molecular biology. — 2002. — Vol. 319, no. 5. — P. 1059—1066. — doi:10.1016/S0022-2836(02)00308-X. — PMID 12079347. [исправить]
  17. ↑ Knudsen B., Hein J. Pfold: RNA secondary structure prediction using stochastic context-free grammars. (англ.) // Nucleic acids research. — 2003. — Vol. 31, no. 13. — P. 3423—3428. — PMID 12824339. [исправить]
  18. ↑ Ruan J., Stormo G. D., Zhang W. ILM: a web server for predicting RNA secondary structures with pseudoknots. (англ.) // Nucleic acids research. — 2004. — Vol. 32. — P. 146—149. — doi:10.1093/nar/gkh444. — PMID 15215368. [исправить]
  19. ↑ Bernhart S. H., Hofacker I. L. From consensus structure prediction to RNA gene finding. (англ.) // Briefings in functional genomics & proteomics. — 2009. — Vol. 8, no. 6. — P. 461—471. — doi:10.1093/bfgp/elp043. — PMID 19833701. [исправить]
  20. ↑ Sankoff D. Simultaneous solution of the RNA folding, alignment and protosequence problems // SIAM Journal on Applied Mathematics. — 1985. — Vol. 45, № 5. — P. 810—825. Архивировано 13 июня 2007 года.
  21. ↑ 1 2 Hofacker I. L., Bernhart S. H., Stadler P. F. Alignment of RNA base pairing probability matrices. (англ.) // Bioinformatics. — 2004. — Vol. 20, no. 14. — P. 2222—2227. — doi:10.1093/bioinformatics/bth229. — PMID 15073017. [исправить]
  22. ↑ Havgaard J. H., Lyngsø R. B., Stormo G. D., Gorodkin J. Pairwise local structural alignment of RNA sequences with sequence similarity less than 40%. (англ.) // Bioinformatics. — 2005. — Vol. 21, no. 9. — P. 1815—1824. — doi:10.1093/bioinformatics/bti279. — PMID 15657094. [исправить]
  23. ↑ Torarinsson E., Havgaard J. H., Gorodkin J. Multiple structural alignment and clustering of RNA sequences. (англ.) // Bioinformatics. — 2007. — Vol. 23, no. 8. — P. 926—932. — doi:10.1093/bioinformatics/btm049. — PMID 17324941. [исправить]
  24. ↑ Mathews D. H., Turner D. H. Dynalign: an algorithm for finding the secondary structure common to two RNA sequences. (англ.) // Journal of molecular biology. — 2002. — Vol. 317, no. 2. — P. 191—203. — doi:10.1006/jmbi.2001.5351. — PMID 11902836. [исправить]
  25. ↑ Harmanci A. O., Sharma G., Mathews D. H. Efficient pairwise RNA structure prediction using probabilistic alignment constraints in Dynalign. (англ.) // BMC bioinformatics. — 2007. — Vol. 8. — P. 130. — doi:10.1186/1471-2105-8-130. — PMID 17445273. [исправить]
  26. ↑ Holmes I. Accelerated probabilistic inference of RNA structure evolution. (англ.) // BMC bioinformatics. — 2005. — Vol. 6. — P. 73. — doi:10.1186/1471-2105-6-73. — PMID 15790387. [исправить]
  27. ↑ Kiryu H., Tabei Y., Kin T., Asai K. Murlet: a practical multiple alignment tool for structural RNA sequences. (англ.) // Bioinformatics. — 2007. — Vol. 23, no. 13. — P. 1588—1598. — doi:10.1093/bioinformatics/btm146. — PMID 17459961. [исправить]
  28. ↑ Shapiro B. A., Zhang K. Z. Comparing multiple RNA secondary structures using tree comparisons. (англ.) // Computer applications in the biosciences : CABIOS. — 1990. — Vol. 6, no. 4. — P. 309—318. — PMID 1701685. [исправить]

Литература

[править | править код]
  • Р. Дурбин, Ш. Эдди, А. Крог, Г. Митчисон. Анализ биологических последовательностей.. — М.-Ижевск.: НИЦ "Регулярная и хаотическая динамика", Институт компьютерных исследований, 2006. — 480 с. — ISBN 5-93972-559-7.


Источник — https://ru.wikipedia.org/w/index.php?title=Предсказание_вторичной_структуры_РНК&oldid=133811961