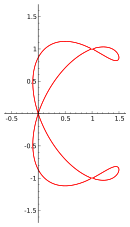
Плоская кривая четвёртой степени (Hlkvtgx tjnfgx cymf~jmkw vmyhyun)

Плоская кривая четвёртой степени или плоская квартика — плоская алгебраическая кривая четвёртой степени. Она может быть определена уравнением четвёртой степени от двух переменных:

$Ax^{4}+By^{4}+Cx^{3}y+Dx^{2}y^{2}+Exy^{3}+Fx^{3}+Gy^{3}+Hx^{2}y+Ixy^{2}+Jx^{2}+Ky^{2}+Lxy+Mx+Ny+P=0,$

Амперсанд

Боб

Двукаспидная кривая

Бант

Крестообразная кривая с параметрами (b,a) = (1,1) - красная; (2,2) - зелёная; (3,3) - синяя.

Крестообразная кривая с параметрами (b,a) = (1,1) - красная; (2,1) - зелёная; (3,1) - синяя.

Семейство спирических сечений

Трёхлистный клевер в декартовых координатах

Трёхлистный клевер в полярных координатах

где по меньшей мере одно из чисел A, B, C, D, E не равно нулю. Это уравнение имеет 15 констант. Однако уравнение можно умножить на любую ненулевую константу без изменения кривой. Таким образом, путём подходящего выбора константы умножения, любой коэффициент можно сделать равным 1, оставляя лишь 14 констант. Таким образом, пространство квартик можно отождествить с вещественным проективным пространством $\mathbb {R} \mathrm {P} ^{14}$. Отсюда также следует по теореме Крамера о алгебраических кривых, что существует в точности одна квартика, проходящая через 14 различных точек общего положения, поскольку квартика имеет 14 степеней свободы.

Квартика может иметь максимум

• четыре связные компоненты
• двадцать четыре бикасательные
• три обыкновенные двойные точки.

Можно рассматривать кривые четвёртой степени над другими полями (или даже кольцами), например, над комплексными числами. В последнем случае получают римановы поверхности, которые являются одномерными объектами над C, но двумерными над R. Примером является квартика Клейна. Кроме того, можно рассматривать кривые в проективной плоскости, задаваемые однородными многочленами.

Примеры

Различные комбинации коэффициентов в уравнении выше дают различные важные семейства кривых, перечисленные ниже.

• Двурогая кривая
• Пулевидная кривая
• Овал Декарта
• Овал Кассини
• Дельтоида
• Лемниската Бута
• Кривая Евдокса
• Квартика Кляйна

• Лемниската
  • Лемниската Бернулли
  • Лемниската Жероно
• Улитка Паскаля
• Квартика Люрота
• Кривая Персея
• Квадружность
  • Специальная квартика Ламэ
• Торическое сечение
• Кривая Тротта

Амперсанд (кривая)

Кривая-амперсанд — это плоская кривая четвёртой степени с уравнением

$\ (y^{2}-x^{2})(x-1)(2x-3)=4(x^{2}+y^{2}-2x)^{2}.$

Кривая имеет род нуль с тремя обыкновенными двойными точками на вещественной плоскости.

Боб (кривая)

Кривая-боб — это плоская кривая четвёртой степени с уравнением

$x^{4}+x^{2}y^{2}+y^{4}=x(x^{2}+y^{2}).\,$

Боб имеет род нуль. Кривая имеет одну особенность в начале координат, обыкновенную тройную точку.

Двукаспидная кривая

Двукаспидная кривая — это плоская кривая четвёртой степени с уравнением

$(x^{2}-a^{2})(x-a)^{2}+(y^{2}-a^{2})^{2}=0\,$,

где a определяет размер кривой. Двукаспидная кривая имеет только две узловые точки в качестве сингулярностей, а потому является кривой рода один.

Бант (кривая)

Бант — это плоская кривая четвёртой степени с уравнением

$x^{4}=x^{2}y-y^{3}.\,$

Бант имеет одну тройную точку в x=0, y=0, а потому является рациональной кривой рода нуль .

Крестообразная кривая

Крестообразная кривая или кривая-крест — это плоская кривая четвёртой степени, задаваемая уравнением

$x^{2}y^{2}-b^{2}x^{2}-a^{2}y^{2}=0\,$,

где a и b — два параметра, определяющие форму кривой. Крестообразная кривая связана стандартным квадратичным преобразованием x ↦ 1/x, y ↦ 1/y с эллипсом $a^{2}x^{2}+b^{2}y^{2}=1$, а потому является рациональной плоской алгебраической кривой рода нуль. Крестообразная кривая имеет три двойные точки на вещественной проективной плоскости в точках x=0 и y=0, x=0 и z=0, y=0 и z=0.

Поскольку кривая является рациональной, она может быть параметризована рациональными функциями. Например, если a=1 и b=2, то уравнения

$x=-{\frac {t^{2}-2t+5}{t^{2}-2t-3}},\quad y={\frac {t^{2}-2t+5}{2t-2}}$

задают параметризацию точек на кривой, кроме исключительных случаев, когда знаменатель обращается в нуль.

Спирическое сечение

Основная статья: Кривая Персея

Спирическое сечение можно определить как бициркулярную кривую четвёртой степени, симметричную относительно осей x и y. Спирические сечения входят в семейство торических сечений и содержат семейство лемнискат Бута и семейство овалов Кассини. Название происходит от греческого слова σπειρα, означающего тор.

В декартовых координатах уравнение можно записать

$(x^{2}+y^{2})^{2}=dx^{2}+ey^{2}+f,$

а в полярных координатах как

$r^{4}=dr^{2}\cos ^{2}\theta +er^{2}\sin ^{2}\theta +f.\,$

Трёхлистный клевер

Трёхлистный клевер — это плоская кривая четвёртой степени

$x^{4}+2x^{2}y^{2}+y^{4}-x^{3}+3xy^{2}=0.\,$

Разрешив уравнение относительно y, получим следующую функцию

$y=\pm {\sqrt {\frac {-2x^{2}-3x\pm {\sqrt {16x^{3}+9x^{2}}}}{2}}},$

где два знака $\pm$ не зависят друг от друга, что даёт до четырёх различных значений y для каждого x.

Параметрическим уравнением трёхлистного клевера будет

$x=\cos(3t)\cos t,\quad y=\cos(3t)\sin t.\,$.

В полярных координатах ($x=r\cos(\varphi ),y=r\sin(\varphi )$) уравнение принимает вид

$r=\cos(3\varphi ).\,$

Кривая является частным случаем розы с k = 3. Эта кривая имеет тройную точку в начале координат (0, 0) и имеет три двойные касательные.