Бикасательная (>ntgvgmyl,ugx)
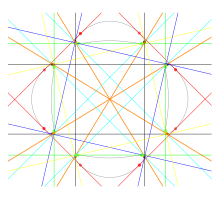
Бикасательная — касательная к заданной кривой, соприкасающаяся с ней ровно в двух точках.
В общем случае у алгебраической кривой через каждую точку проходит касательная, но только конечное число из них могут быть бикасательными. По теореме Безу любая имеющая бикасательную алгебраическая кривая имеет степень 4 или выше. Доказательство теоремы о 28 бикасательных плоской кривой четвёртой степени стало важным звеном в развитии геометрии XIX века благодаря тому, что он оказался тесно связан с результатом о 27 прямых на кубике.
Четыре прямых, каждая из которых касается пары выпуклых многоугольников, можно легко найти с помощью двоичного поиска. Именно, в этом алгоритме нужно поддерживать пару указателей в списки рёбер, а затем переводить один и указателей влево или вправо, в зависимости от того, как проходит ребро, среднее между указателями. Подобный поиск бикасательных часто применяется в структурах данных, используемых для эффективного хранения и изменения выпуклых оболочек[англ.][1]. В 1990-е годы описан основанный на псевдотриангуляции[англ.] алгоритм, эффективно перечисляющий все отрезки, бикасательные к семейству выпуклых кривых и не пересекающие ни одной кривой[2].
Также поиск бикасательных может применяться для ускорения основанного на графах видимости подхода к нахождению кратчайшего пути в евклидовой метрике: кратчайший путь среди выпуклых препятствий должен огибать их, проходя по бикастаельным всюду, кроме границ. Это позволяет найти кратчайший путь с помощью алгоритма Дейкстры к подграфу графа видимости, образованному лежащими на бикасательных рёбрами[3].
Связанные понятия
[править | править код]Секущая, в отличие от бикасательной, может пересекать кривую в тех точках, через которые она проходит. Также можно рассматривать бикасательные кривые; например, срединная ось кривой ― множество центров окружностей, касающихся кривой в более чем одной точке.
Касательные прямые к двум окружностям используются в описанном Якобом Штейнером в 1826 году построении окружностей Мальфатти, при вычислении длины верёвки, соединяющей два блока[англ.], в теореме Кейси о четырёх окружностях, касающихся пятой, а также в теореме Монжа о коллинеарности точек пересечения бикасательных.
Примечания
[править | править код]Литература
[править | править код]- M. H. Overmars, J. van Leeuwen. Maintenance of configurations in the plane // Journal of Computer and System Sciences. — 1981. — Т. 23, вып. 2. — С. 166–204. — doi:10.1016/0022-0000(81)90012-X.
- M. Pocchiola, G. Vegter. The visibility complex // International Journal of Computational Geometry and Applications. — 1996. — Т. 6, вып. 3. — С. 297–308. — doi:10.1142/S0218195996000204.
- M. Pocchiola, G. Vegter. Topologically sweeping visibility complexes via pseudotriangulations // Discrete and Computational Geometry. — 1996. — Т. 16, вып. 4. — С. 419–453. — doi:10.1007/BF02712876.
- H. Rohnert. Shortest paths in the plane with convex polygonal obstacles // Information Processing Letters. — 1986. — Т. 23, вып. 2. — С. 71–76. — doi:10.1016/0020-0190(86)90045-1.