Период колебаний (Hyjnk; tklyQgunw)

Период
Период
Размерность	T
Единицы измерения
СИ	с

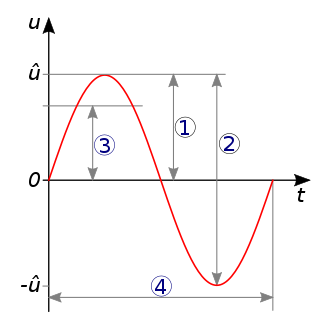
Пери́од колеба́ний — наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние^[1], в котором она находилась в первоначальный момент, выбранный произвольно).

В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическим колебаниям (а приближённо — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идёт о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Обозначения: обычное стандартное обозначение периода колебаний: $T$ (хотя могут применяться и другие, наиболее часто это $\tau$ , иногда $\Theta$ и т. д.).

Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.

Период колебаний связан соотношением взаимной обратности с частотой:

T={\frac {1}{\nu }},\ \ \ \nu ={\frac {1}{T}}.

Для волновых процессов период связан кроме того очевидным образом с длиной волны $\lambda$

v=\lambda \nu ,\ \ \ T={\frac {\lambda }{v}},

где $v$ — скорость распространения волны (точнее^[2] — фазовая скорость).

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота^[3] колебаний его волновой функции).

Теоретическое вычисление периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближённо — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощрённые методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идёт о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Периоды колебаний в природе

Представление о периодах колебаний различных физических процессов даёт статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).

Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот электромагнитных колебаний (см. Электромагнитный спектр) .

Периоды колебаний слышимого человеком звука находятся в диапазоне

от 5·10⁻⁵с до 0,2с

(чёткие границы его несколько условны).

Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне

от 1,1·10⁻¹⁵с до 2,3·10⁻¹⁵с.

Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать чёткую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжёлой из известных сейчас частиц.

В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено^[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху — время существования Вселенной — более десяти миллиардов лет.

Периоды колебаний простейших физических систем

Пружинный маятник

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

$T=2\pi {\sqrt {\frac {m}{k}}}$ ,

где $m$ — масса груза, $k$ — жёсткость пружины.

Математический маятник

Период малых колебаний математического маятника:

$T=2\pi {\sqrt {\frac {l}{g}}}$

где $l$ — длина подвеса (к примеру, нити), $g$ — ускорение свободного падения. Отсюда видно, что период колебаний маятника зависит только от длины подвеса и ничего более.

Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью^[5] равен 2 секундам.

Физический маятник

Период малых колебаний физического маятника:

$T=2\pi {\sqrt {\frac {J}{mgl}}}$

где $J$ — момент инерции маятника относительно оси вращения, $m$ — масса маятника, $l$ — расстояние от оси вращения до центра масс.

Крутильный маятник

Период колебаний крутильного маятника:

$T=2\pi {\sqrt {\frac {I}{K}}}$

где $I$ — момент инерции маятника относительно оси кручения, а $K$ — вращательный коэффициент жёсткости маятника.

Электрический колебательный (LC) контур

Период колебаний электрического колебательного контура (формула Томсона):

$T=2\pi {\sqrt {LC}}$ ,

где $L$ — индуктивность катушки, $C$ — ёмкость конденсатора.

Эту формулу вывел в 1853 году английский физик Уильям Томсон.

Примечания

↑ Состояние механической системы характеризуется положениями и скоростями всех её материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству её степеней свободы).
↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение также верно.
↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания её волновой функции (а значит обратна периоду этого колебания).
↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
↑ Лучше, чем 0,5 %, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53 % для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.

Ссылки

[bse.sci-lib.com/article088257.html Период колебаний] — статья из Большой советской энциклопедии

[1] Состояние механической системы характеризуется положениями и скоростями всех её материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству её степеней свободы).

[2] Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение также верно.

[3] С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания её волновой функции (а значит обратна периоду этого колебания).

[4] Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.

[5] Лучше, чем 0,5 %, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53 % для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.

[1]

[2]

[3]

[4]

[5]