Шифр Цезаря (Onsj Ey[gjx)

Шифр Цезаря со сдвигом на 3:
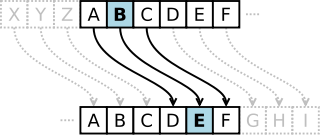
A заменяется на D
B заменяется на E
и так далее
Z заменяется на C

Шифр Цезаря (лат. Notae Caesarianae), также известный как шифр сдвига или код Цезаря — разновидность шифра подстановки, в котором каждый символ в открытом тексте заменяется символом, находящимся на некотором постоянном числе позиций левее или правее него в алфавите (так, в шифре со сдвигом вправо на 3, А была бы заменена на Г, Б станет Д, и так далее. Шифр был назван в честь римского полководца Гая Юлия Цезаря, использовавшего его для секретной переписки со своими военачальниками. Шаг шифрования, выполняемый шифром Цезаря, часто включается как часть более сложных схем, таких как шифр Виженера, и всё ещё имеет современное приложение в системе ROT13. Как и все моноалфавитные шифры, шифр Цезаря легко взламывается и не имеет почти никакого применения на практике. Тем не менее, он считается одним из самых простых и наиболее широко известных методов шифрования.

Математическая модель

Если сопоставить каждому символу алфавита его порядковый номер (нумеруя с 0), то шифрование и дешифрование можно выразить формулами модульной арифметики:

$y=(x+k)\ \mod \ n$

$x=(y-k)\ \mod \ n,$

где $x$ — символ открытого текста, $y$ — символ шифрованного текста, $n$ — мощность алфавита, а $k$ — ключ.

С точки зрения математики шифр Цезаря является частным случаем аффинного шифра.

Пример

Шифрование с использованием ключа $k=3$. Буква «Е» «сдвигается» на три буквы вперёд и становится буквой «З». Твёрдый знак, перемещённый на три буквы вперёд, становится буквой «Э», буква «Я», перемещённая на три буквы вперёд, становится буквой «В», и так далее:

Исходный алфавит: А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я
Шифрованный:      Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я А Б В 

Оригинальный текст:

Съешь же ещё этих мягких французских булок да выпей чаю.

Шифрованный текст получается путём замены каждой буквы оригинального текста соответствующей буквой шифрованного алфавита:

Фэзыя йз зьи ахлш пвёнлш чугрщцкфнлш дцосн жг еютзм ъгб.

Пример для языков программирования

Python

Код написан и выполняется для 2 языков: русского и английского.

 # Текст, который пользователь хочет ввести
text = input("Введите текст, который хотите зашифровать: ")
# Пользователь вводит ключ
k = int(input("Укажите ключ: "))
# Пользователь вводит язык текста, который будет зашифрован
language = input("На каком языке текст, который вы ввели (русский, английский): ")

# Функция шифрования с тремя параметрами: текст, ключ, язык
def ceaser_cipher(user, key, lang):
    # Переменная результата шифрования; переменная, определяющая верхний и нижний регистр
    res, n = [], ""

    # Проверка пользователем выбранного языка

    # Проверка выбран ли русский язык (регистр букв, вводимых пользователем, не важен)
    if lang.lower() in ["русский", "russian"]:
        # Двум переменным присваиваются русская азбука нижнего и верхнего регистра соответственно
        dictionary, dictionary_upper = "абвгдеёжзийклмнопрстуфхцчшщъыьэюя", "АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ"
    # Проверка выбран ли английский язык (регистр букв, вводимых пользователем, не важен)
    elif lang.lower() in ["английский", "english"]:
        # Двум переменным присваиваются английской азбука нижнего и верхнего регистра соответственно
        dictionary, dictionary_upper = "abcdefghijklmnopqrstuvwxyz", "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
    else:
        return "Такого языка нет в опции"

    # Цикл проверки, где каждую итерацию будет обрабатываться один символ из текста последовательно
    for i in range(len(user)):
        # Проверка символа на верхний или нижний регистр

        # Принадлежит ли символ нижнему регистру
        if user[i] in dictionary:
            n = dictionary
        # Принадлежит ли символ верхнему регистру
        elif user[i] in dictionary_upper:
            n = dictionary_upper
        # Символ не принадлежит ни нижнему ни верхнему регистру (символ не является буквой)
        else:
            res.append(user[i])

        # Если символ есть в списке n (является буквой), то будет происходить его зашифровка
        if user[i] in n:
            # Цикл перебора азбуки
            for j in range(len(n)):
                # Если порядковый номер буквы + ключ находятся в диапазоне от 0 до конца азбуки
                # и если буква из текста совпадает с буквой из азбуки, то:
                if 0 <= j + key < len(n) and user[i] == n[j]:
                    # В результат добавляется буква со сдвигом key (зашифрованная буква)
                    res.append(n[j + key])
                # Если порядковый номер буквы + ключ выходит из диапазона азбуки, превышая его
                # и если буква из текста совпадает с буквой из азбуки, то:
                elif j + key >= len(n) and user[i] == n[j]:
                    # В результат добавляется буква со сдвигом key,
                    # при этом переводя порядковый номер буквы к диапазону азбуки (зашифрованная буква)
                    res.append(n[(1 - j - key) % (len(n) - 1)])
                # Если порядковый номер буквы + ключ выходит из диапазона азбуки, недотягивает до него
                # и если буква из текста совпадает с буквой из азбуки, то:
                elif j + key < 0 and user[i] == n[j]:
                    # В результат добавляется буква со сдвигом key,
                    # при этом приводя порядковый номер буквы к диапазону азбуки (зашифрованная буква)
                    res.append(n[(j + key) % len(n)])

    # Функция возвращает зашифрованный текст
    return ''.join(res)

# Вывод зашифрованного текста
print(ceaser_cipher(text, k, language))

История и применение

Шифр Цезаря назван в честь Гая Юлия Цезаря, который использовал его с левым сдвигом на 3

Шифр Цезаря называют в честь Юлия Цезаря, который, согласно «Жизни двенадцати цезарей» Светония, использовал его со сдвигом 3, чтобы защищать военные сообщения. Хотя Цезарь был первым зафиксированным человеком, использовавшим эту схему, другие шифры подстановки, как известно, использовались и ранее.

Если у него было что-либо конфиденциальное для передачи, то он записывал это шифром, то есть так изменял порядок букв алфавита, что нельзя было разобрать ни одно слово. Если кто-либо хотел дешифровать его и понять его значение, то он должен был подставлять четвертую букву алфавита, а именно, D, для A, и так далее, с другими буквами.
Гай Светоний Транквилл Жизнь двенадцати цезарей, Книга первая, гл. 56

Его племянник, Август, также использовал этот шифр, но со сдвигом вправо на один, и он не повторялся к началу алфавита:

Всякий раз, когда он записывал шифром, он записал B для A, C для B, и остальной части букв на том же самом принципе, используя AA для X.
Гай Светоний Транквилл Жизнь двенадцати цезарей, Книга вторая, гл. 88

Есть доказательства, что Юлий Цезарь использовал также и более сложные схемы.

Неизвестно, насколько эффективным шифр Цезаря был в то время, но, вероятно, он был разумно безопасен, не в последнюю очередь благодаря тому, что большинство врагов Цезаря было неграмотным, и многие предполагали, что сообщения были написаны на неизвестном иностранном языке. Нет никаких свидетельств того времени касательно методов взлома простых шифров подстановки. Самые ранние сохранившиеся записи о частотном анализе — это работы Ал-Кинди 9-го века об открытии частотного анализа.

Шифр Цезаря со сдвигом на один используется на обратной стороне мезузы, чтобы зашифровать имена Бога. Это может быть пережитком с раннего времени, когда еврейскому народу не разрешили иметь мезузы.

В XIX веке личная секция рекламных объявлений в газетах иногда использовалась, чтобы обмениваться сообщениями, зашифрованными с использованием простых шифров. Кан (1967) описывает случаи, когда любители участвовали в секретных коммуникациях, зашифрованных с использованием шифра Цезаря в «Таймс». Даже позднее, в 1915, шифр Цезаря находил применение: российская армия использовала его как замену для более сложных шифров, которые оказались слишком сложными для войск; у немецких и австрийских криптоаналитиков были лишь небольшие трудности в расшифровке этих сообщений.

Шифр Цезаря со сдвигом тринадцать также используется в алгоритме ROT13, простом методе запутывания текста, широко используемом в Usenet'е, и используется скорее как способ сокрытия спойлеров, чем как метод шифрования. Шифр Виженера использует шифр Цезаря с различными сдвигами в каждой позиции в тексте; значение сдвига определяется с помощью повторяющегося ключевого слова. Если ключевое слово такое же длинное, как и сообщение, сгенерировано случайным образом, содержится в тайне и используется лишь однократно — такая схема называется схема одноразовых блокнотов — и это единственная система шифрования, для которой доказана абсолютная криптографическая стойкость.

Ключевые слова короче, чем сообщение (например, «Complete Victory», использовавшееся Конфедерацией во время гражданской войны в США), вводят циклический образец, который мог бы быть обнаружен с помощью улучшенной версии частотного анализа.

В апреле 2006 беглый босс сицилийской мафии Бернардо Провенцано был пойман в Сицилии частично из-за криптоанализа его сообщений, написанных с использованием вариации шифра Цезаря. В шифре Провенцано буквы сначала заменялись на числа — порядковые номера букв в алфавите, а уже к полученной последовательности чисел применялся шифр Цезаря — так, чтобы при сдвиге на 3 «A» была написана как «4», «B» — как «5», и так далее.

Часто для удобства использования шифра Цезаря используют два насаженных на общую ось диска разного диаметра с нарисованными по краям дисков алфавитами. Изначально диски поворачиваются так, чтобы напротив каждой буквы алфавита внешнего диска находилась та же буква алфавита малого диска. Если теперь повернуть внутренний диск на несколько символов, то мы получим соответствие между символами внешнего диска и внутреннего — шифр Цезаря. Получившийся диск можно использовать как для шифрования, так и для расшифровки.

Например, если внутреннее колесо повернуть так, чтобы символу A внешнего диска соответствовал символ D внутреннего диска, то мы получим шифр со сдвигом 3 влево.

Взлом шифра

Сдвиг де- шифровки	Открытый текст
0	exxegoexsrgi
1	dwwdfndwrqfh
2	cvvcemcvqpeg
3	buubdlbupodf
4	attackatonce
5	zsszbjzsnmbd
6	yrryaiyrmlac
…
23	haahjrhavujl
24	gzzgiqgzutik
25	fyyfhpfytshj

Шифр Цезаря может быть легко взломан даже в случае, когда взломщик знает только зашифрованный текст. Можно рассмотреть две ситуации:

1. Взломщик знает (или предполагает), что использовался простой шифр подстановки, но не знает, что это — схема Цезаря.
2. Взломщик знает, что использовался шифр Цезаря, но не знает значение сдвига.

В первом случае шифр может быть взломан, используя те же самые методы что и для простого шифра подстановки, такие как частотный анализ и т. д. Используя эти методы, взломщик, вероятно, быстро заметит регулярность в решении и поймёт, что используемый шифр — это шифр Цезаря.

Распределение букв в типичном образце текста на английском языке имеет характерный и предсказуемый вид. Шифр Цезаря «поворачивает» это распределение, и возможно определить сдвиг, проверяя график частотностей для каждого из возможных сдвигов

Во втором случае взлом шифра является даже более простым. Существует не так много вариантов значений сдвига (26 для английского языка), все они могут быть проверены методом грубой силы. Один из способов сделать это — выписать отрывок зашифрованного текста в столбец всех возможных сдвигов — техника, иногда называемая как «завершение простого компонента». Рассмотрим пример для зашифрованного текста «EXXEGOEXSRGI»; открытый текст немедленно опознается глазом в четвертой строке.

Другой способ применения этого метода — это написать алфавит под каждой буквой зашифрованного текста, начиная с этой буквы. Метод может быть ускорен, если использовать заранее подготовленные полоски с алфавитом. Для этого нужно сложить полоски так, чтобы в одной строке образовался зашифрованный текст, тогда в некоторой другой строке мы увидим открытый текст.

Другой подход к применению метода грубой силы для взлома — проверить частотности букв. Изобразив диаграммой частотности букв в зашифрованном тексте, и зная ожидаемое распределение букв для обычного текста на рассматриваемом языке, можно легко определить сдвиг, взглянув на смещение некоторых характерных черт на диаграмме. Этот метод известен как частотный анализ. Например, в тексте на английском языке частотность букв E, T, (обычно наиболее частых), и Q, Z (обычно более редких) особенно различаются. Этот процесс можно автоматизировать, сделав, чтобы компьютерная программа оценивала, насколько хорошо фактическое распределение частотностей соответствует ожидаемому распределению. Например, может использоваться критерий хи-квадрат.

Для обычного текста на естественном языке, скорее всего, будет только один вариант декодирования. Но, если использовать очень короткие сообщения, то возможны случаи, когда возможны несколько вариантов расшифровки с различными сдвигами. Например зашифрованный текст «MPQY» может быть расшифрован как «aden» так и как «know» (предполагая, что открытый текст написан на английском языке). Точно также «ALIIP» можно расшифровать как «dolls» или как «wheel»; «AFCCP» как «jolly» или как «cheer» (см. также расстояние единственности).

Многократное шифрование никак не улучшает стойкость, так как применение шифров со сдвигом a и b эквивалентно применению шифра со сдвигом a + b. В математических терминах шифрование с различными ключами образует группу.

Литература

• Гай Светоний Транквилл. Жизнь двенадцати цезарей = De vita XII caesarvm. — М.: Издательство «Наука», 1964. — 374 с. — (Литературные памятники).
• Kahn D. The Codebreakers (англ.): The Story of Secret Writing — Macmillan, 1967. — 1164 p. — ISBN 978-0-684-83130-5
• Singh S. The Code Book, Histoire des codes secrets (англ.): The Science of Secrecy from Ancient Egypt to Quantum Cryptography, De l'Égypte des pharaons à l'ordinateur quantique — New York City: Doubleday, Knopf Doubleday Publishing Group, 1999. — 416 p.
• Фомичёв В. М. Дискретная математика и криптология: Курс лекций / под ред. Н. Д. Подуфалов — М.: Диалог-МИФИ, 2013. — 397 с. — ISBN 978-5-86404-185-7
• Wobst R. Cryptology Unlocked (англ.) / A. Shafir — Chichester: John Wiley & Sons Ltd, 2007. — 554 p. — ISBN 978-0-470-06064-3

Ссылки

• Caesar cipher — реализация шифра Цезаря на разных языках на Rosetta Code.
• Шифр Цезаря - шифрование и дешифровка