Теорема о пяти окружностях (Mykjybg k hxmn ktjr'ukvmx])

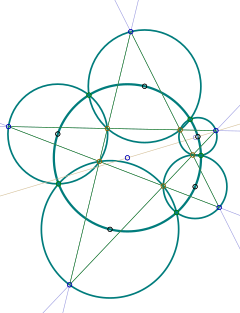
Теорема о пяти окружностях утверждает: пусть дана цепочка из пяти окружностей, и каждые две соседние из них пересекаются; также дана шестая окружность, которой принадлежат центры пяти окружностей и одна из точек пересечения каждой пары соседних окружностей (та точка, которая дальше от центра шестой окружности); тогда прямые, соединяющие точки пересечения, ближайшие к центру этой шестой окружности, образуют пентаграмму, вершины которой лежат на этих пяти окружностях.

См. также

• Теоремы Клиффорда
• Теорема Микеля
• Теорема Микеля о шести окружностях
• Теорема о шести окружностях
• Теорема о семи окружностях
• Теорема о пяти кругах

Литература

• Wells D. The Penguin Dictionary of Curious and Interesting Geometry. — New York: Penguin Books, 1991. — С. 79. — ISBN 0-14-011813-6.

Ссылки

• Weisstein, Eric W. Miquel Five Circles Theorem (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Miquel Pentagram Theorem (англ.) на сайте Wolfram MathWorld.