Распределение арксинуса (Jgvhjy;ylyuny gjtvnurvg)
| Арксинус | |
|---|---|
 Плотность вероятности Плотность вероятности | |
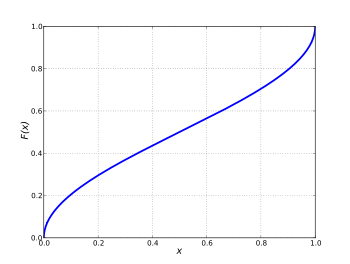 Функция распределения Функция распределения | |
| Параметры | none |
| Носитель | |
| Плотность вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Дифференциальная энтропия | |
| Производящая функция моментов | |
| Характеристическая функция | |
Распределение арксинуса (англ. arcsine distribution) — распределение вероятностей, функция распределения которого имеет вид
при 0 ⩽ x ⩽ 1, а плотность вероятности равна
на (0, 1). Стандартное распределение арксинуса является частным случаем бета-распределения при α = β = 1/2. Таким образом, если представляет собой стандартное распределение арксинуса, то .
Обобщение
[править | править код]| Носитель с произвольными границами | |
|---|---|
| Параметры | |
| Носитель | |
| Плотность вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
Распределение арксинуса можно обобщить на случай произвольного ограниченного носителя a ⩽ x ⩽ b с помощью простого преобразования
при a ⩽ x ⩽ b. Плотность вероятности задаётся функцией
на (a, b).
Обобщённое стандартное распределение арксинуса на (0, 1) с плотностью распределения
представляет собой частный случай бета-распределения с параметрами .
Заметим, что при обобщённое распределение арксинуса приводится к указанному выше виду.
Свойства
[править | править код]- Распределение арксинуса замкнуто относительно сдвига и масштабирования на положительный множитель:
- если , то
- Квадрат распределения арксинуса на (−1, 1) обладает распределением арксинуса на (0, 1):
- если , то
Связанные распределения
[править | править код]- Если U и V независимые и одинаково равномерно распределённые случайные величины на (−π, π), то , , , и обладают распределением .
- Если — обобщённое распределение арксинуса с параметром на носителе [a, b], тогда
Примечания
[править | править код]- Rogozin, B.A. (2001) [1994], "A/a013160", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
На эту статью не ссылаются другие статьи Википедии. |
![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)














![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)



















