Потенциал Сазерленда (Hkmyuengl Vg[yjlyu;g)
Потенциал Сазерленда[ссылка 1][ссылка 2] (Sutherland potential) — простая модель парного взаимодействия неполярных молекул, описывающая зависимость энергии взаимодействия двух частиц от расстояния между ними. Впервые этот вид потенциала был предложен Уильямом Сазерлендом[англ.] в 1893 году. Потенциал сочетает в себе твердую сердцевину (бесконечно сильное отталкивание на близких расстояниях) с притягивающим хвостом, описываемым степенным законом. Эта модель относительно реалистично передаёт свойства реального взаимодействия сферических неполярных молекул и поэтому широко используется в расчётах и при компьютерном моделировании.
Вид потенциала взаимодействия
[править | править код]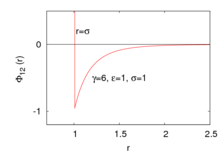
Обобщённая форма потенциала Сазерленда описывается следующим образом:
где — потенциал парного взаимодействия[англ.][комментарий 1], — расстояние между частицами 1 и 2, положение которых описывается радиусом-вектором . — глубина потенциальной ямы, — радиус соответствующей твёрдой сферы, — параметр, контроллирующий скорость убывания потенциала до нуля.
На больших расстояниях данный потенциал является притягивательным
Отталкивание частиц происходит лишь на расстояниях, с бесконечной силой.
Общая форма взаимодействия между атомами или молекулами включает в себя отталкивающую часть на малых расстояниях и притягивающую часть на больших расстояниях. В качестве аналитического представления взаимодействия часто используется потенциал потенциала Леннарда-Джонса 6-12. Притягательный хвост, являющийся следствием флуктуаций электрических дипольных моментов, хорошо описывается законом . Однако описание отталкивающего центра является простым приближением степенного закона к реальному взаимодействию на близких расстояниях. Популярность потенциала 6-12 заключается, главным образом, в его математической элегантности. Потенциал Сазерленда рассматривает отталкивание на коротких расстояниях по-другому; он аппроксимирует взаимодействие в виде жесткого ядра. Притягивающий хвост описывается обычным дипольным законом .
| Газ | Из измеренной вязкости | Из измеренной самодиффузии | ||
|---|---|---|---|---|
| 2.33 | 192 | 2.20 | 196 | |
| 3.07 | 416 | 3.17 | 202 | |
| 3.43 | 638 | — | — | |
Вириальные коэффициенты
[править | править код]
| Коэффициент | Значение коэффициента |
|---|---|
| 0.625 | |
| -0.6448603 | |
| 0.2861417 | |
| 0.0709195 | |
| 0.0027382 | |
| -0.0062834 | |
| -0.0035694 | |
| -0.0013018 | |
| -0.0003808 | |
| -0.0000961 | |
| -0.0000217 |
Второй вириальный коэффициент
[править | править код]Второй вириальный коэффициент данного потенциала можно выразить в следующем виде[ссылка 5]
где — приведённая температура, а — обобщённая неполная гамма-функция:
Как известно, в общем виде второй вириальный коэффициент можно записать как
Подставим выражение потенциала Сазерленда
Сделаем подстановку и
Разложим экспоненту в ряд по степеням и почленно проинтегрируем
В результате получим, что второй вириальный коэффициент данного потенциала можно выразить в следующем виде
В высокотемпературном пределе второй вириальный коэффициент потенциала Сазерленда стремится к значению для потенциала твёрдых сфер[англ.]:
при этом основное его изменение линейно, в отличие от, например, потенциала Леннарда-Джонса, который не имеет столь простого поведения при , что является следствием «размягчения» твёрдого ядра. Отметим, что при .
Связь параметров уравнения Ван-дер-Ваальса с параметрами потенциала
Параметры уравнения Ван-дер-Ваальса можно связать с параметрами потенциала Сазерленда следующим образом[ссылка 6]:
В выражении для второго вириального коэффициента разложим экспоненту в ряд, ограничившись только первыми двумя слагаемыми
Обратим внимание, что получившийся интеграл сходится только при
Учитывая, что для уравнения Ван-дер-Ваальса
Получим выражения для параметров уравнения:
Случай
При второй вириальный коэффициент возможно выразить как
где — комплексная функция ошибок[англ.].
Температура Бойля и температура инверсии могу быть найдены из своих определений:
Третий вириальный коэффициент
[править | править код]Третий вириальный коэффициент данного потенциала может быть получен в виде разложения[ссылка 7] по степеням :
где — коэффициенты, первые 11 из которых приведены в таблице.
Закон Сазерленда
[править | править код]| 2 | 0.2662 | 0.2336 |
| 3 | 0.2276 | 0.2118 |
| 4 | 0.2010 | 0.1956 |
| 6 | 0.1667 | 0.1736 |
| 8 | 0.1444 | 0.1556 |
| Газ | , мкпз | , 1 атм. |
|---|---|---|
| 137 | 254 | |
| 166 | 101 | |
| 93 | 503 | |
| 116 | 306 | |
| 116 | 331 | |
| 171 | 375 | |
| 133 | 360 | |
| 173 | 390 | |
| 179 | 128 | |
| 107 | 290 | |
| 188 | 83 | |
| 298 | 61 | |
| 210 | 142 | |
| 233 | 210 | |
| 211 | 290 | |
| 123 | 351 | |
| 146 | 533 | |
| 85 | 73 | |
| 137 | 260 | |
| 165 | 104 | |
| 192 | 125 |
Используя метод Чепмена—Энскога можно получить следующее выражение для динамической вязкости газа и коэффициента самодиффузии :
где — осреднённое сечение потери энергии, — усреднённое диффузионное сечение потери импульса.
Точный расчет углов отклонения и эффективных сечений столкновения требует трудоемкой вычислительной работы. Однако если предположить, что притяжение относительно слабо, то высшими степенями , которые появляются при точном подходе к проблеме, можно пренебречь. В результате получим формулы Сюзерленда для вязкости и диффузии, широко используемые для получения кривых, соответствующих экспериментальным данным
где — динамическая вязкость и коэффициент диффузии модели твёрдых сфер.
а — постоянная Сазерленда, пропорциональная энергии взаимодействия двух молекул при их соприкосновении:
Данные соотношения лежат в основе полу-эмпирической формулы, носящей название закона Сазерленда, позволяющей рассчитать вязкость при температуре по известной вязкости при опорной температуре :
За опорную температуру обычно принимают 273.15K. Так, данные для воздуха , дают хорошую аппроксимацию в диапазоне температур . При этом подразумевается, что постоянная Сазерленда практически не зависит от температуры: для воздуха , .
При отсутствии данных по можно использовать следующую аппроксимацию:
где — температура кипения.
Сазерленд пришёл к этой зависимости при анализе экспериментально измеренной вязкости газа от температуры, впервые обратив внимание на зависимость газокинетического диаметра молекулы от температуры:
где — диаметр Стюарта, соответствующий размеру молекул при
Примечания
[править | править код]Комментарии
- ↑ Intermolecular pair potential Архивная копия от 23 декабря 2023 на Wayback Machine on SklogWiki Архивная копия от 8 января 2020 на Wayback Machine.
- ↑ Бекман И. Н. Курс лекций Мембраны в медицине. — М., 2010.
Источники
- ↑ William Sutherland. The viscosity of gases and molecular force // Philosophical Magazine. — 1893. — Т. 36. — С. 507—531. Архивировано 23 декабря 2023 года.
- ↑ H. W. Graben and R. D. Present. Third Virial Coefficient for the Sutherland (∞, ν) Potential // Reviews of Modern Physics. — 1964. — Т. 36. — С. 1025—1033. Архивировано 23 декабря 2023 года.
- ↑ Дж. Гиршфельдер, Ч. Кертисс и Р. Берд. Молекулярная теория газов и жидкостей / перевод с английского под редакцией Е.В. Ступоченко. — М.: Издательство иностранной литературы, 1961. — 931 с.
- ↑ H. W. Graben and R. D. Present. Third Virial Coefficient for the Sutherland (∞, ν) Potential // Reviews of Modern Physics. — 1964. — Т. 36. — С. 1025—1033. Архивировано 23 декабря 2023 года.
- ↑ D. Levi and M. de Llano. Closed form of second virial coefficient for Sutherland potential // J. Chem. Phys. — 1975. — Т. 63. — С. 4561—4562.
- ↑ J. Tian and Y. Gui. Modification to the Van der Waals Equation of State // J. phase equilib. — 2003. — Т. 24. — С. 533—541.
- ↑ H. W. Graben and R. D. Present. Third Virial Coefficient for the Sutherland (∞, ν) Potential // Reviews of Modern Physics. — 1964. — Т. 36. — С. 1025—1033. Архивировано 23 декабря 2023 года.
- ↑ Дж. Гиршфельдер, Ч. Кертисс и Р. Берд. Молекулярная теория газов и жидкостей / перевод с английского под редакцией Е.В. Ступоченко. — М.: Издательство иностранной литературы, 1961. — 931 с.
Литература
[править | править код]- William Sutherland. The viscosity of gases and molecular force // Philosophical Magazine Series 5. — 1893. — Декабрь (т. 36, № 223). — С. 507—531.
- Дж. Гиршфельдер, Ч. Кертисс и Р. Берд. Молекулярная теория газов и жидкостей / перевод с английского под редакцией Е.В. Ступоченко. — М.: Издательство иностранной литературы, 1961. — 931 с.
- Каплан И. Г. Введение в теорию межмолекулярных взаимодействий.. — М.: Наука. Главная редакция физико-математической литературы, 1982. — С. 312.
- M. P. Allen, D. J. Tildesley. Computer Simulation of Liquids. — Oxford University Press, 1990. — ISBN 0198556454. — ISBN 9780198556459.
- Цянь Сюэ-Сень. Физическая механика. — М.: Мир, 1965. — 544 с.
- D. Levi and M. de Llano. Closed form of second virial coefficient for Sutherland potential // Journal of Chemical Physics. — 1975. — Т. 63. — С. 4561—4562.
- Jianxiang Tian and Yuanxing Gui. Liquid-gas phase transition to first order of an argon-like fluid modeled by the hard-core similar Sutherland potential // International Journal of Modern Physics B. — 2004. — Т. 18. — С. 2057—2069.
- A. Díez, J. Largo and J. R. Solana. Structure and thermodynamic properties of Sutherland fluids from computer simulation and the Tang–Lu integral equation theory // Fluid Phase Equilibria. — 2007. — № 253. — С. 67—73.
- Jianguo Mi, Yiping Tang, and Chongli Zhong. Theoretical study of Sutherland fluids with long-range, short-range, and highly short-range potential parameters // Journal of Chemical Physics. — 2008. — Т. 128. — С. 054503.
- Roman Melnyk, Pedro Orea, Ivo Nezbeda, and Andrij Trokhymchuk. Liquid/vapor coexistence and surface tension of the Sutherland fluid with a variable range of interaction: Computer simulation and perturbation theory studies // Journal of Chemical Physics. — 2010. — № 132. — С. 134504.
- F. Paragand, F. Feyzi and B. Behzadi. Application of the SAFT-VR equation of state to vapor–liquid equilibrium calculations for pure components and binary mixtures using the Sutherland potential // Fluid Phase Equilibria. — 2010. — Т. 290. — С. 181—194.
- J. Tian and Y. Gui. Modification to the Van der Waals Equation of State // J. phase equilib. — 2003. — Т. 24. — С. 533—541.

































![{\displaystyle B_{2}(T)=-2\pi \int _{0}^{\infty }r^{2}\left(\exp \left[-{\frac {\Phi _{ij}(r)}{kT}}\right]-1\right)dr}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca020a2ae976534f3cf0dcedd4d744185eda2223)
![{\displaystyle B_{2}(T)=-2\pi \int _{0}^{\infty }r^{2}\left(\exp \left[-{\frac {\Phi _{ij}(r)}{kT}}\right]-1\right)dr=2\pi \int _{0}^{\sigma }r^{2}dr-2\pi \int _{\sigma }^{\infty }r^{2}\left(\exp \left[{\frac {\varepsilon }{kT}}\left({\frac {\sigma }{r}}\right)^{\gamma }\right]-1\right)dr={\frac {2}{3}}\pi \sigma ^{3}-2\pi \int _{\sigma }^{\infty }r^{2}\left(\exp \left[{\frac {\varepsilon }{kT}}\left({\frac {\sigma }{r}}\right)^{\gamma }\right]-1\right)dr}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a27f1f088af9b93a0472148cba0f0ed3df9a6064)

![{\displaystyle B_{2}(\tau )/{\frac {2}{3}}\pi \sigma ^{3}=1-3\int _{1}^{\infty }x^{2}\left(\exp \left[{\frac {1}{\tau x^{\gamma }}}\right]-1\right)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e47ab79218ed36764443d4392c0335fb3871ea47)








![{\displaystyle \exp \left[{\frac {1}{\tau x^{\gamma }}}\right]=1+{\frac {1}{\tau x^{\gamma }}}+...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0cc594e8746b34966607da6407ce44cf028ef83)




















































