Окружности Джонсона (Ktjr'ukvmn :'kuvkug)

Теорема Джонсона утверждает, что если три синие окружности на рисунке имеют один и тот же радиус и все три проходят через точку H, то получающаяся красная окружность имеет тот же радиус, что и синие окружности. Зелёный треугольник ΔJ_AJ_BJ_C является тогда треугольником Джонсона чёрного треугольника ΔABC и имеет описанную окружность (оранжевая) радиуса r.

Набор окружностей Джонсона состоит из трёх окружностей одинакового радиуса r, имеющих одну общую точку пересечения H. В такой конфигурации окружности обычно имеют четыре точки пересечения (точки, через которые проходят по меньшей мере две окружности) — это общая точка пересечения H, через которую проходят все три окружности, и по дополнительной точке для каждой пары окружностей (будем о них говорить как о попарных пересечениях). Если любые две окружности не пересекаются (а только лишь касаются) они имеют лишь одну общую точку — H, и в этом случае считается, что H является и их попарной точкой пересечения также. Если же окружности совпадают, принимается за попарную точку пересечения точка, диаметрально противоположная точке H. Три точки попарных пересечений окружностей Джонсона образуют опорный треугольник Δ ABC фигуры. Конфигурация названа именем Роджера Артура Джонсона.

Замечание

Если исходный опорный треугольник ABC остроугольный и заранее задан, то в силу теоремы Гамильтона три его окружности Джонсона одинаковых радиусов являются просто тремя описанными окружностями трех треугольников Гамильтона, имеющими в качестве двух вершин две вершины данного опорного треугольника ABC, а в качестве третьей вершины ортоцентр H опорного треугольника.

Свойства

Антикомплементарная окружность (красная, радиус 2R) треугольника ΔABC касается трёх окружностей Джонсона, и центры окружностей лежат на отрезках (оранжевые), соединяющих общую точку пересечения H и точки касания. Точки касания образуют антикомплементарный треугольник, ΔP_AP_BP_C (зелёный).

1. Центры окружностей Джонсона лежат на окружности того же радиуса R, что и окружности Джонсона, и эта окружность имеет центром точку H. Сами же центры окружностей формируют треугольник Джонсона ΔJ_AJ_BJ_C.
2. Окружность радиуса 2R с центром в точке H, известная как антикомплементарная окружность, касается всех трёх окружностей Джонсона (R - радиус описанной окружности треугольника ABC ). Три точки касания являются отражениями точки H относительно вершин треугольника Джонсона.
3. Точки касания окружностей Джонсона и антикомплементарной окружности образуют треугольник, носящий название «антикомплементарный треугольник» или «антидополнительный треугольник» опорного (исходного) треугольника ABC. Этот треугольник подобен треугольнику Джонсона и гомотетичен ему с множителем 2 и центром подобия H.
4. Теорема Джонсона: Точки попарных пересечений окружностей Джонсона (вершины треугольника ABC) лежат на окружности того же радиуса R, что и окружности Джонсона. Это свойство хорошо известно в Румынии как задача пяти монет Георге Цицейки.
5. Опорный треугольник равен треугольнику Джонсона и гомотетичен ему с множителем −1. То есть треугольник Джонсона переходит в опорный треугольник поворотом одного из них на угол 180 градусов относительно их центра подобия.
6. Точка H является ортоцентром опорного треугольника и центром описанной окружности треугольника Джонсона.
7. Центр подобия треугольника Джонсона и опорного треугольника является их общим центром девяти точек. То есть треугольник Джонсона и опорный треугольник имеют общую окружность девяти точек.
8. Замечание. Вершины треугольника Джонсона обозначены через J_A, J_B и J_C, то есть также, как и центры вневписанных окружностей опорного треугольника. Они таковыми не являются. В силу теоремы о трезубце для центра $J_{B}$ вневписанной окружности, касающейся стороны $AC$, имеем $|DI|=|DA|=|DC|=|DJ_{B}|$, где $I$ центр вписанной окружности опорного треугольника, $D$ — точка пересечения биссектрисы угла $A$ с описанной окружностью треугольника $ABC$. У нас выполняется аналогичное соотношение $|J_{A}H|=|J_{A}C|=|J_{A}B|=|J_{A}P_{A}|$. Однако точка $J_{A}$ не лежит на описанной окружности треугольника $ABC$ (то есть не является аналогом точки $D$), а ортоцентр $H$ не является центром $I$ вписанной окружности опорного треугольника.

Замечание

H — ортоцентр треугольника ABC (тогда в силу теоремы Гамильтона радиусы окружностей Джонсона равны). O — центр описанной окружности треугольника ABC. Как и теорема Гамильтона, теорема Джонсона имеет смысл только для остроугольных треугольников. Точки J_A, J_B и J_C обозначены по первой букве фамилии Johnson, и не являются центрами вневписанных окружностей треугольника ABC, которые обозначаются аналогичными буквами.

Доказательства

Свойство 1 очевидно из определения.

Свойство 2 также понятно — для любой окружности радиуса r и любой точки P на ней окружность с радиусом 2r и центром в P касается окружности в точке, противоположной точке P. В частности, это верно и для P=H, где окружность радиуса 2r— антикомплементарная окружность C.

Свойство 3 немедленно следует из определения подобия.

Для свойств 4 и 5 сначала заметим, что любые две окружности Джонсона из трёх симметричны относительно прямой, проходящей через точку H и точку попарных пересечений этих окружностей (или относительно общей касательной в H, если эти точки совпадают) и эта симметрия обменивает местами две вершины антикомплементарного треугольника, лежащих на этих окружностях. Таким образом, попарные точки пересечения являются серединами антикомплементарного треугольника, и H лежит на перпендикуляре к середине этой стороны. Средние точки сторон любого треугольника являются образами вершин треугольника при гомотетии с множителем  −½ и центром, совпадающим с центром тяжести треугольника. Применяя это свойство к антикомплементарному треугольнику, который сам получается из треугольника Джонсона гомотетией с множителем  2, из композиции гомотетий получим, что опорный треугольник подобен треугольнику Джонсона с множителем −1. Поскольку такая гомотетия является конгруэнтностью, это даёт свойство 5, а также доказывает теорему Джонсона, поскольку равные треугольники имеют равные радиусы описанных окружностей.

Свойство 6. Уже установлено, что перпендикуляры к серединам сторон антикомплементарного треугольника проходят через точку H. Вследствие того, что эти стороны параллельны сторонам опорного треугольника, эти перпендикуляры являются также высотами опорного треугольника.

Свойство 7 немедленно следует из свойства 6, поскольку центр подобия с множителем -1 должен лежать посередине между центром описанной окружности O опорного треугольника и точкой H. Точка H является ортоцентром опорного треугольника и его центр девяти точек, как известно, является этой серединой. Ввиду центральной симметрии, отображающей ортоцентр опорного треугольника в ортоцентр треугольника Джонсона, центр подобия является также центром девяти точек треугольника Джонсона.

Имеется также алгебраическое доказательство теоремы окружностей Джонсона, использующее простые векторные формулы. Имеются вектора ${\vec {u}}$, ${\vec {v}}$ и ${\vec {w}}$, все длины r, и окружности Джонсона имеют центры в точках $H+{\vec {u}}$, $H+{\vec {v}}$ и $H+{\vec {w}}$ соответственно. Тогда попарными пересечениями будут $H+{\vec {u}}+{\vec {v}}$, $H+{\vec {u}}+{\vec {w}}$ и $H+{\vec {v}}+{\vec {w}}$ соответственно, и ясно, что точка $H+{\vec {u}}+{\vec {v}}+{\vec {w}}$ имеет расстояние r до любой попарной точки пересечения.

Дальнейшие свойства

Три окружности Джонсона можно рассматривать как отражения описанной вокруг опорного треугольника окружности относительно его трёх сторон. Более того, при отражении ортоцентр H переходит в три точки на описанной вокруг опорного треугольника окружности, формируя вершины ортокругового треугольника, центр описанной окружности O отображается в вершины треугольника Джонсона, а его прямая Эйлера (прямая, проходящая через O, N и H) образует три прямых, пересекающихся в точке X(110).

Описанный эллипс Джонсона

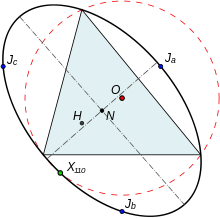
Треугольник Джонсона и его опорный треугольник имеют совпадающие центры девяти точек, ту же самую прямую Эйлера и те же самые окружности девяти точек. Шесть точек — вершины опорного треугольника и вершины его треугольника Джонсона — лежат на эллипсе Джонсона, имеющем центр в центре девяти точек и точка X(216) опорного треугольника является его точкой перспективы. Описанный эллипс и описанная окружность имеют четыре общие точки — три вершины опорного треугольника и точку X(110).

И, наконец, существуют две интересные и описанные в литературе кубические кривые, проходящие через вершины опорного треугольника и его треугольника Джонсона, а также через центр описанной окружности, ортоцентр и центр девяти окружностей. Первая кривая известна как кривая Муссельмана — K026. Эта кривая проходит также через вершины срединного треугольника и срединного треугольника треугольника Джонсона. Вторая кривая известна как кривая центров Эйлера — K044. Эта кривая также проходит через шесть точек — основания высот и основания высот треугольника Джонсона.

Обозначение точки X(i) принадлежит классификации Кларка Кимберлинга (Clark Kimberling) в энциклопедии точек треугольника.

Литература

• Roger Arthur Johnson. Modern Geometry:An Elementary Treatise on the Geometry of the Triangle and the Circle. — Houghton: Mifflin Company, 1929.
• Roger Arthur Johnson. A Circle Theorem // American Mathematical Monthly. — 1916. — Вып. 23.

Ссылки

• Weisstein, Eric W. Johnson Theorem (англ.) на сайте Wolfram MathWorld.
• F. M. Jackson and Weisstein, Eric W. Johnson Circles (англ.) на сайте Wolfram MathWorld.
• F. M. Jackson and Weisstein, Eric W. Johnson Triangle (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Johnson Circumconic (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Anticomplementary Triangle (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Circum-Orthic Triangle (англ.) на сайте Wolfram MathWorld.
• Bernard Gibert Circumcubic K026 Архивная копия от 19 марта 2007 на Wayback Machine
• Bernard Gibert Circumcubic K044
• Clark Kimberling, "Encyclopedia of triangle centers Архивная копия от 19 апреля 2012 на Wayback Machine". (Lists some 3000 interesting points associated with any triangle.)