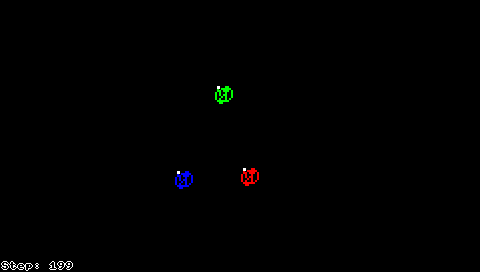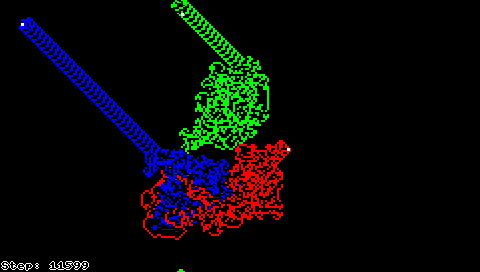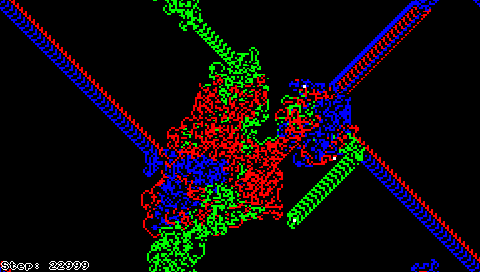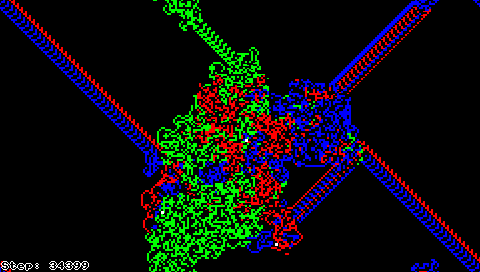
Муравей Лэнгтона (Brjgfyw Lzuimkug)

Муравей Лэнгтона — это двумерный клеточный автомат с очень простыми правилами, изобретенный Крисом Лэнгтоном. Муравья можно также считать двумерной машиной Тьюринга с 2 символами и 4 состояниями.

После 11000 шагов (красный пиксель — местонахождение муравья)

Правила

Первые 200 шагов

Муравей выбирается из квадрата

Рассмотрим бесконечную плоскость, разбитую на клетки, покрашенные некоторым образом в чёрный и белый цвет. Пусть в одной из клеток находится «муравей», который на каждом шаге может двигаться в одном из четырёх направлений в клетку, соседнюю по стороне. Муравей движется согласно следующим правилам:

• На чёрном квадрате — повернуть на 90° влево, изменить цвет квадрата на белый, сделать шаг вперед на следующую клетку.
• На белом квадрате — повернуть на 90° вправо, изменить цвет квадрата на чёрный, сделать шаг вперед на следующую клетку.

Эти простые правила вызывают довольно сложное поведение: после некоторого периода довольно случайного движения муравей, видимо, начинает непременно строить дорогу из 104 шагов, повторяющуюся бесконечно, независимо от изначальной раскраски поля. Это наводит на мысль, что «магистральное» поведение является стабильным аттрактором муравья Лэнгтона. Является ли «магистраль» единственным аттрактором при перемещении муравья?

Муравей Лэнгтона также может быть описан как клеточный автомат, в котором почти всё поле покрашено в чёрно-белый цвет, а клетка с «муравьём» имеет один из восьми различных цветов, кодирующих соответственно все возможные комбинации чёрного/белого цвета клетки и направления движения муравья.

Расширение муравья Лэнгтона

Существует простое расширение муравья Лэнгтона, в котором используется более двух цветов клеток. Цвета изменяются циклически. Для таких муравьев существует также простая форма названия: для каждого следующего цвета используется буква L или R (Л и П), в зависимости от того, поворачивает ли муравей направо или налево. Таким образом, муравей Лэнгтона — это муравей RL.

Некоторые из этих обобщенных муравьев Лэнгтона рисуют узоры, которые становятся все более симметричными. Один из простых примеров — муравей RLLR. Одно достаточное условие этого заключается в том, что имя муравья, рассматриваемое как циклический список, состоит из последовательных пар повторяющихся букв LL или RR (цикличность списка означает, что последняя буква может спариваться с первой).

Также добавлена буква N, которая означает, что муравей не будет поворачиваться и просто пройдёт вперёд.

• Примеры:
• 
  RLR: Хаотичный рост
• 
  LLRR: Симметричный рост
• 
  LRRRRRLLR: Заполняет пространство в квадрате вокруг себя
• 
  LLRRRLRLRLLR: Создаёт извилистую магистраль
• 
  RRLLLRLLLRRR
• 
  L2NNL1L2L1: Гексагональное поле, рост по кольцу
• 
  L1L2NUL2L1R2: Гексагональное поле, спиральный рост
• 
  R1R2NUR2R1L2: Анимация
• 
  LN: Горизонтальный рост

На гексагональном поле существует 6 различных поворотов, которые обозначены здесь как N (без изменений), R1 (60° по часовой стрелке), R2 (120° по часовой стрелке), U (180°), L2 (120° против часовой стрелки), L1 (60° против часовой стрелки).

Тьюрмиты

• Примеры:
• 
  Спиральный рост
• 
  Полухаотичный рост
• 
• 
• 
• 

См. также

• Тьюрмиты

Литература

• David Darling. The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes. — John Wiley & Sons, 2004. — P. 180–181. — ISBN 978-0-471-27047-8.
• Иэн Стюарт. Величайшие математические задачи. — М.: Альпина нон-фикшн, 2016. — 460 с. — ISBN 978-5-91671-507-1.

Ссылки

• Further Travels with my Ant, D. Gale, J. Propp, S. Sutherland, и S. Troubetzkoy: статья в форматах PostScript или TeX, содержащая доказательство указанного выше достаточного условия симметричности узора.
• https://web.archive.org/web/20070601034903/http://www.theory.org/software/ant/
• http://www.math.sunysb.edu/~scott/ants/
• http://yoda.neostrada.pl/ ASM32 приложение с возможностями увеличения, добавления препятствий, сохранения/загрузки, обращения цветов, пошаговым режимом
• https://web.archive.org/web/20020223080004/http://www.fortunecity.com/emachines/e11/86/langton.html Колонка Математических Развлечений в Scientific American, использующая муравья Лэнгтона как метафору для Теории Великого Объединения