Моделирование твёрдого тела (Bk;ylnjkfguny mf~j;kik mylg)

Геометрия объёмного моделирования полностью описывает трёхмерный объект. Объекты можно рассматривать под любым углом.

Моделирование твёрдого тела — это непротиворечивый набор принципов математического и компьютерного моделирования трёхмерных объектов. Моделирование твёрдого тела отличается от близких областей, геометрического моделирования и компьютерной графики, упором на физическую точность. Принципы геометрического моделирования и моделирования твёрдого тела вместе образуют основу систем автоматизированного проектирования трёхмерных тел и, как правило, поддерживают создание, визуализацию, анимацию, вычисление и аннотацию численных свойств модели физических объектов. На протяжении статьи будем употреблять термины «твёрдое тело», «сплошное тело» и «трёхмерное тело» как синонимы.

Обзор

Использование техник объёмного моделирования позволяет автоматизацию некоторых сложных инженерных вычислений, выполняемых как часть процесса разработки. Моделирование, планирование и проверка процессов, таких как обработка резанием и конвейерная сборка, были главными катализаторами развития моделирования объёмного тела. Недавно был расширен ряд производственных приложений такими процессами, как производство изделий из листового металла, литьё пластмасс под давлением, сварка, прокладка труб и так далее. Кроме традиционного производства, техники объёмного моделирования обеспечивают фундамент для быстрого прототипирования, архивации цифровых данных и обратной разработки путём построения тел из отобранных точек на физических объектах, механический анализ с использованием метода конечных элементов, планирования движения и проверка пути NC (араг. Numerical Control, Числовое управление), кинематический и динамический анализ механизмов, и так далее. Центральной задачей всех этих приложений является возможность эффективно представлять трёхмерные геометрические объекты и работать с ними согласно физическому поведению реальных объектов.

Математические основы

Понятие объёмного моделирования в современном понимании опирается на конкретные нужды для информационной полноты в системах механического геометрического моделирования, в том смысле, что любая компьютерная модель должна поддерживать все геометрические запросы, которые могут быть сформулированы для соответствующего физического объекта. Требование наявности отражает возможность нескольких компьютерных представлений одного и того же физического объекта пока эти два представления совместимы. Невозможно вычислительно проверить информационную полноту представления, пока понятие физического объекта не определено в терминах математически вычисляемых свойств, независимых от конкретного представления. Эти причины привели к разработке парадигм моделирования, которые очерчивают поле объёмного моделирования в том виде, какое мы сейчас имеем.

Все создаваемые компоненты имеют конечный размер и хорошо определённые границы, так что первоначально фокус был направлен на математическое моделирование твёрдых частей, сделанных из однородного изотропного материала, который может быть добавлен или удалён. Эти постулируемые свойства можно транслировать в свойства подмножеств трёхмерного евклидова пространства. Два общих подхода для определения твёрдости опирается на общую топологию и алгебраическую топологию соответственно. Обе модели определяют, как твёрдое тело может быть построено из простых кусков или ячеек.

Регуляризация двумерного множества путём замыкания внутренности

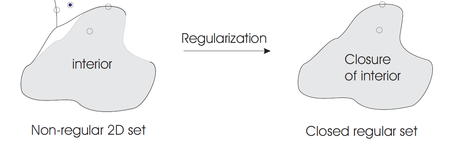
Согласно неразрывной модели точечных множеств все точки любого множества $X\subset \mathbb {R} ^{3}$ можно классифицировать по их окрестности по отношению к X как внутренность, внешность и граница. При предположении, что пространство $\mathbb {R} ^{3}$ снабжено типичной евклидовой метрикой, окрестность точки $p\in X$ принимает форму открытого шара. Чтобы признать X сплошным, необходимо, чтобы любая окрестность любой точки $p\in X$ была трёхмерной. Точки с окрестностями меньшей величины означают потерю цельности объекта. Однородность по размерности окрестностей гарантирована для класса замкнутых регулярных множеств, определённых как множества, равные замыканию их внутренности. Любое множество $X\subset \mathbb {R} ^{3}$ может быть преобразовано в замкнутое регулярное множество (регуляризовано) путём замыкания его внутренности, а потому пространство моделирования цельных объектов математически определяется как пространство замкнутых регулярных подмножеств $\mathbb {R} ^{3}$ (по теореме Гейне — Бореля из этого следует, что все сплошные тела являются компактными множествами). Кроме того требуется, чтобы сплошные тела были замкнуты относительно операций над множествами: объединение, пересечение и разность (чтобы гарантировать свойство твёрдости после добавления или удаления материала). Применение стандартных булевых операций к регулярным множествам может не дать замкнутое регулярное множество, но эта проблема может быть решена путём регуляризации результата стандартных булевых операций . Регуляризованные операции над множествами обозначаются как $\cup ^{\ast },\cap ^{\ast }$ и $-^{\ast }$.

Комбинаторное описание множества $\mathbb {R} ^{3}$ как сплошного использует представление X в виде ориентированного клеточного комплекса, так что ячейки обеспечивают конечные пространственные адреса для точек в несчётном континууме. Класс полуаналитических ограниченных подмножеств евклидова пространства замкнут относительно булевых операций (стандартных и регуляризованных) и обладает дополнительным свойством — любое полуаналитическое множество может быть стратифифировано на набор непересекающихся ячеек размерностей 0,1,2,3. Триангуляция полуаналитического множества в набор точек, отрезков, треугольных граней и тетраэдральных элементов является часто применяемым примером стратификации. Комбинаторная модель твёрдости затем завершается указанием, что вдобавок к требованию, чтобы подмножества были полуаналитичными и ограниченными, требуется, чтобы тела были трёхмерными топологическими иногогранниками, в частности, трёхмерными ориентируемыми многообразиями с краем. В частности, из этого следует, что эйлерова характеристика комбинаторной границы многогранника равна 2. Комбинаторная многообразная модель сплошного тела гарантирует также, что граница тела разбивает пространство в точности на две компоненты как следствие теоремы Жордана — Брауэра, тем самым исключая множества с немногообразными окрестностями, которые считаются невозможными для изготовления.

Точечная и комбинаторные модели твёрдых тел полностью совместимы друг с другом, могут использоваться взаимозаменяемо, опираясь на свойства непрерывности или на комбинаторные свойства по необходимости, и могут быть распространены на любую размерность n. Основное свойство, обеспечивающее эту совместимость, заключается в том, что класс замкнутых регулярных подмножеств $\mathbb {R} ^{n}$ в точности совпадает с однородно n-мерными топологическими многогранниками. Поэтому любое n-мерное тело может быть однозначно представлено его границей, а граница имеет комбинаторную структуру n−1-мерного многогранника, имеющего однородных n−1-мерных соседей.

Схемы представлений

Любая схема представления трёхмерных тел, основанная на принятых математических свойствах, является методом фиксации информации о классе полуаналитических подмножеств евклидового пространства. Это означает, что все представления являются различными способами организации одних и тех же геометрических и топологических данных в форме структуры данных. Все схемы представлений организованы в терминах конечного числа операций над множеством примитивов. Таким образом, пространство моделирования любого конкретного представления конечно, а любая отдельная схема представления может оказаться недостаточной для представления всех типов объектов. Например, трёхмерные тела, определённые комбинациями регуляризованных булевых операций, не могут быть всегда представлены как выметание примитивом, движущемся по траектории в пространстве, за исключением очень простых случаев. Это вынуждает современные системы геометрического моделирования поддерживать несколько схем представлений объёмных тел и позволять эффективное преобразование из одной схемы в другую.

Ниже приведён список общих техник, используемых для создания или представления моделей твёрдых тел. Современное программное обеспечение моделирования может использовать комбинацию этих схем для представления трёхмерного тела.

Клонирование примитивов

Эта схема основывается на понятии семейств объектов, в которых каждый член семейства отличается от другого члена лишь несколькими параметрами. Каждое семейство объектов называется основным примитивом, а индивидуальные объекты семейства называются представителями примитивов. Например, семейство болтов является основным примитивом, а конкретный болт, удовлетворяющий определённому набору параметров, является представителем примитива. Различающиеся характеристики простых схем параметрической конкретизации мешают комбинировать частные варианты примитивов для представления новых более сложных объектов. Другим главным недостатком этой схемы является сложность написания алгоритмов вычисления свойств представляемого схемой тел. Приличное количество специфичной для семейства информации должно быть встроено в алгоритмы, а потому каждый общий примитив должен обрабатываться специальным образом, не позволяющим единообразного подхода.

Нумерация пространственного заполнения

Схема нумерации пространственного заполнения (англ. Spatial occupancy enumeration), по существу, является списком пространственных ячеек, занятых телом. Ячейки, которые называются также вокселами, представляют собой кубики фиксированного размера, которые расположены в фиксированной пространственной решётке (возможны и другие многогранные решётки, но решётка кубов самая простая). Каждая ячейка может быть представлена координатами одной точки, например, центром куба. Обычно предполагается определённый порядок просмотра и соответствующее упорядоченное множество координат называется пространственным массивом (англ. spatial array). Пространственные массивы являются ясными и однозначными представлениями трёхмерных тел, но они слишком велики для использования в качестве «главного» или определяющего представления. Они могут, однако, представлять грубую аппроксимацию частей и могут быть использованы для улучшения производительности геометрических алгоритмов, особенно в случае, когда они используются вместе с другими представлениями, такими как конструктивная сплошная геометрия.

Сотовая декомпозиция

Эта схема проистекает из комбинаторных (алгебраических и топологических) описаний сплошных тел, разобранных выше. Тело может быть представлено его разбиением на ячейки. Схемы нумерации пространственного заполнения являются частным случаем сотовых декомпозиций, в которых все ячейки являются кубиками, лежащими в регулярной решётке. Сотовые декомпозиции обеспечивают удобный способ вычисления некоторых топологических свойств сплошных объектов, таких как связность (число кусков) и род (число дыр). Сотовые декомпозиции в виде триангуляризаций являются представлениями, используемыми в трёхмерном методе конечных элементов для числового решения дифференциальных уравнений в частных производных. Другие сотовые декомпозиции, такие как регулярная стратификация Уитни или декомпозиции Морса, могут быть использованы для приложений в планировании движения робота.

Граничное представление

Основная статья: Граничное представление

В этой схеме трёхмерное тело представлено путём разложения на ячейки его границы. Поскольку границы твёрдого тела имеют свойство разбивать пространство, согласно теореме Жордана — Брауэра, обсуждаемой выше, на внутренность тела и дополняющее её внешнее пространство, любая точка в пространстве может быть проверена однозначно путём тестирования её относительно границы тела. Вспомним, что возможность проверить любую точку тела гарантирует, что тело будет сплошным. С помощью процедуры «ray casting» можно подсчитать число пересечений луча границ тела. Чётное число пересечений соответствует внешним точкам, а нечётное число пересечений соответствует внутренним точкам. Допущение, что границы являются сотовыми комплексами многообразий, вынуждает любое граничное представление удовлетворять условию отсутствия пересечения различных примитивов, то есть, нет самопересечений, которые образуют точки, не принадлежащие многообразиям. В частности, из условия многообразности вытекает, что все пары вершин разъединены (не совпадают), пары рёбер либо не пересекаются, либо имеют общую вершину, а пары граней либо не пересекаются, либо имеют общее ребро. Было разработано несколько структур данных, являющихся комбинаторными картами, для хранения граничных представлений твёрдых тел. Кроме плоских граней современные системы обеспечивают возможность сохранить поверхности второго порядка и поверхности NURBS как части границ представления. Граничные представления используются в качестве схем представления сплошных тел в большинстве коммерческих геометрических систем моделирования ввиду их гибкости в представлении тел, имеющих высокую сложность.

Моделирование сетки поверхности

Схема подобна граничному представлению представляется поверхность тела. Однако, вместо сложных структур данных и NURBS используется простая сетка вершин и рёбер. Поверхностные сетки могут быть структурированными (как треугольные сетки в STL-файлах или четырёхугольные сетки с горизонтальными и вертикальными кольцами четырёхугольников) или не структурированными со случайными группами треугольников и других многоугольников.

Конструктивная блочная геометрия

Основная статья: Конструктивная сплошная геометрия

Конструктивная сплошная геометрия (КСГ, англ. Constructive solid geometry, CSG) — это семейство схем для представления твёрдых тел как булевых конструкций или комбинаций примитивов с помощью регуляризованных операций над множествами, которые обсуждались выше. КСГ и граничные представления в настоящее время являются наиболее важными схемами для представления сплошных тел. КСГ-представления принимают вид упорядоченных двоичных деревьев, в которых нетерминальный узел представляет либо жёсткие преобразования (сохраняющие ориентацию изометрии), либо регуляризованные операции над множествами. Конечные узлы являются примитивными листьями, которые представляют замкнутые регулярные множества. Семантика представления КСГ ясна. Каждое поддерево представляет множество, полученное от применения указанных операций преобразования и регуляризованных операций над множествами, представленными примитивными листьями поддерева. КСГ-представления особенно полезны для захвата определяющих параметров в виде свойств, соответствующих добавлению или удалению материала (выступы, дыры, карманы и т.д.). К привлекательным свойствам КСГ относятся лаконичность, гарантированная правильность тел, вычислительно удобные булевы алгебраические свойства и естественный контроль формы тела в терминах параметров высокого уровня, определяя примитивы тела, их положение и ориентацию. Относительно простая структура данных и элегантные рекурсивные алгоритмы дают дополнительную популярность КСГ.

Выметание

Основное понятие, воплощённое в схемах выметания очень просто. Множество движется в пространстве, оставляя след или выметая объём (тело), которое может быть представлено движущимся множеством и траекторией. Такое представление важно в контексте приложений, таких как определение материала, удаляемого резаком, когда он движется по определённой траектории, вычисления динамического столкновения двух движущихся тел, планирование движения и даже в компьютерных графических приложения, таких как отслеживание движения кисти по холсту. Большинство коммерческих систем CAD обеспечивают (ограниченную) функциональность по построению тел выметания главным образом в виде a двумерного сечения, движущегося по пространственной траектории перпендикулярно сечению. Однако текущие исследования показывают некоторые аппроксимации трёхмерных фигур, движущихся согласно одному параметру и даже нескольким параметрам.

Неявное представление

Основная статья: Представление формы функцией

Очень общим методом определения множества X является задание предиката, который может быть применён в любой точке пространства. Другими словами, X определяется неявно состоящим из всех точек, которые удовлетворяют условиям, указанным в предикате. Простейшей формой предиката является условие на знак вещественной функции в знакомом представлении множеств через равенства и неравенства. Например, если $f=ax+by+cz+d$, условия $f(p)=0$, $f(p)>0$ и $f(p)<0$ представляют, соответственно, плоскость и два линейных полупространства. Более сложные функциональные примитивы могут быть определены посредством булевых комбинаций более простых предикатов. Более того, теория R-функций позволяет преобразование таких представлений в одно функциональное неравенство для любого замкнутого полуаналитического множества. Такое представление может быть преобразовано к граничному представлению с помощью алгоритмов полигонизации, например, используя алгоритм «marching cubes».

Параметрическое и основанное на свойствах моделирование

Функциональные элементы определяются как параметрические формы, ассоциированные с атрибутами, такими как неотъемлемые геометрические параметры (длина, ширина, глубина и т.д.), положение и ориентация, геометрические допуски, свойства материалов и ссылки на другие свойства. Функциональные элементы также обеспечивают доступ к связанным производственным процессам и моделям ресурсов. Таким образом, Функциональные элементы семантически имеют более высокий уровень, чем простые замкнутые регулярные множества. Предполагается, что функциональные элементы образуют базис для связи CAD с нижележащими производственными приложениями и для организации баз данных для повторного использования результатов разработки. Моделирование на основе параметрических функциональных элементов часто комбинируется с конструктивной сплошной геометрией для полного описания сложных систем объектов при проектировании.

История моделирования объёмных объектов

Историческое развитие объёмного моделирования следует рассматривать в контексте полной истории CAD, ключевыми вехами которой была разработка системы BUILD с последующим отпочкованием коммерческой системы Romulus, которая в дальнейшем оказала влияние на развитие систем Parasolid, ACIS и систем компании Solid Modeling Solutions. Одна из первых разработчиков CAD в Содружестве Независимых Государств (СНГ), компания ASCON начала внутреннюю разработку своей собственной системы моделирования трёхмерных объектов в 1990-х годах. В ноябре 2012 математическое подразделение ASCON стало самостоятельной компанией и получило название C3D Labs. Этой компании была поставлена задача создания геометрического ядра САПР как самостоятельного продукта, это единственное коммерческое ядро трёхмерного моделирования в России. Другой вклад был получен от Мантюля с его GWB и от проекта GPM, который в начале 1980-х предложил, кроме других вещей, технику гибридного моделирования. Возможно, это подтолкнуло к разработке языка программирования для моделирования трёхмерных тел (англ. Programming Language of Solid Modeling, PLaSM) в римском университете Сапиенца.

Система автоматизированного проектирования

Основная статья: Система автоматизированного проектирования

Моделирование твёрдых тел является минимальным требованием для систем CAD. Разработчики моделей твёрдых тел становятся обыденным явлением в отделах инженерной разработки в последние десять лет вследствие появления более быстрых компьютеров и доступных цен на программное обеспечение. Программное обеспечение моделирования твёрдых тел создаёт виртуальные трёхмерные представления частей для проектирования машин и их анализа. Типичный графический интерфейс пользователя включает макроопределения, клавишные сочетания и динамическое манипулирование моделью. Придаётся особое значение возможности динамически переориентировать модель в пространстве с подрисовыванием теней в реальном времени, что помогает разработчику представить в уме трёхмерный образ.

Модель сборных твёрдых тел состоит из группы деталей, добавляемых по одной, пока модель не будет полной. Производственные модели сплошных тел строятся большей частью на основе эскизных деталей — двухмерные эскизы выставляются вдоль пути, образуя трёхмерный объект. Это могут быть отсечения или вытягивания, например. Проектирование по компонентам обычно осуществляется в контексте всего тела с помощью методов моделирования сборки. Модель сборки включает ссылки на отдельные модели частей, составляющих продукт .

Другой техникой моделирования является «облицовка» (Freeform surface modeling = Моделирование поверхности произвольной формы), техника моделирования в CAD и CAID). В этом случае определяются поверхности, которые обрезаются и склеиваются с целью образования сплошного тела. Поверхности обычно определяются базовыми кривыми в пространстве и набором сложных команд. Облицовка более сложна, но более пригодна для некоторых производственных техник, таких как литьё под давлением. Объёмные модели частей для литья под давлением имеют свойства «облицовки» и моделей на основе эскизов.

Параметрическое моделирование

Основная статья: Параметрическое моделирование

Параметрическое моделирование использует параметры для определения модели (размеры, например). Примерами параметров являются: размеры, используемые для создания деталей модели, плотность материала, формулы для описания пространственного заполнения, импортированные данные (которые описывают поверхность, например). Параметр может быть изменён позже и модель отразит внесённые изменения. Обычно имеется взаимосвязь между частями, узлами и чертежами. Часть состоит из многих деталей, а узел состоит из множества частей. Чертежи могут быть созданы как для частей, так и для узлов.

Пример: Стержень может быть создан путём выдавливания сквозь круглое отверстие на длину 100мм. Головка присоединяется к концу стержня. Позднее длина стержня меняется на 200мм (кликаем на стержень, выбираем длину, заменяем на 200). После обновления модели стержень будет иметь длину 200мм, головка переместится на конец стержня, куда она и прикреплена, инженерная графика и свойства тела будут изменены автоматически.

Основанной на параметрах, но слегка другой является система ограничений. Ограничения — это связь между элементами, образующими конкретную форму. Для окна стороны могут быть определены параллельными и имеющими те же размеры. Параметрическое моделирование очевидно и интуитивно. Однако для первых трёх десятилетий CAD это не было фактом. Модификации означают перерисовку или отрезание или добавление. Размеры в инженерной графике создавались, а не показывались. Параметрическое моделирование является мощным средством, но требует больше навыков для создания моделей. Сложные модели для литья под давлением могут иметь тысячи деталей и исправление ранее добавленной детали может привести к нарушению детали, добавленной позднее. Грамотно созданные параметрические модели легко модифицировать и с ними легко работать. Параметрическое моделирование также поддаётся повторному использованию. Всё семейство болтов может быть заключено в одну модель, например.

Медицинское объёмное моделирование

Современные сканеры компьютерной аксиальной томографии и магнитно-резонансной томографии могут быть использованы для создания моделей объектов внутри тела человека, так называемый объёмный рендеринг. Оптические трёхмерные сканеры могут быть использованы для создания облаков точек или моделей полигональной сетки внешних свойств тела.

Использование медицинского объёмного моделирования;

• Визуализация
• Визуализация отдельных тканей тела (только кровеносных сосудов и опухолей, например)
• Разработка протезов, биопротезов и других медицинских и зубных устройств (это иногда называется массовым производством по индивидуальным заказам)
• Создание моделей полигональной сетки для быстрого прототипирования (для подготовки хирургов к сложным операциям, например)
• Комбинирование моделей полигональной сетки с моделированием твёрдого тела в CAD (разработка запасных частей, например)
• Компьютерный анализ сложных биологических процессов, таких как потоки воздуха и крови
• Компьютерное моделирование новых медицинских устройств и имплантов

Если использование моделирования предназначена для визуализации отсканированных данных, полученных в виде сегментированных изображений или сетки, необходимо генерировать аккуратное и реалистичное геометрическое описание отсканированных данных.

Инженерное моделирование

Окно свойств массы модели в системе Cobalt

Поскольку программы CAD, работающие на компьютерах, «понимают» истинную геометрию составляющих сложных частей, многие атрибуты трёхмерных тел, такие как центр тяжести, объём и масса, могут быть быстро вычислены. Например, для куба со скруглёнными рёбрами, показанный на рисунке вверху статьи, с размером между гранями в 8,4мм, не смотря на много радиусов и мелких пирамид, свойства вычисляются быстро, что показано на приведённом экране (справа).

См. также

• Вычислительная геометрия
• Компьютерная графика
• Инженерная графика
• Эйлерово граничное представление
• PLaSM – Язык программирования для моделирования твёрдых тел (англ. Programming Language of Solid Modeling).
• Чертёж

Ссылки

• sgCore C++/C# library
• The Solid Modeling Association