L-распределение (L-jgvhjy;ylyuny)

L-распределение
Плотность вероятности
Функция распределения
Обозначение	$L(\eta ,\gamma )$
Параметры	$\eta ,\gamma \in (0,\infty )$ — параметры формы
Носитель	$0\leqslant x\leqslant 1$
Плотность вероятности	${\begin{cases}\eta \gamma \left(1-\left(1-x\right)^{\eta }\right)^{\gamma -1}\left(1-x\right)^{\eta -1}&0\leqslant x\leqslant 1\\\\0&\ x<0\ ,\ x>1\end{cases}}$
Функция распределения	${\begin{cases}0&x<0\\\left(1-\left(1-x\right)^{\eta }\right)^{\gamma }&~~~~~0\leqslant x<1\\1&x\geqslant 1\end{cases}}$
Математическое ожидание	$1-{\frac {1}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {1}{\eta }}\right)$
Медиана	$1-\left(1-0.5^{\frac {1}{\gamma }}\right)^{\frac {1}{\eta }}$
Мода	${\begin{cases}1-exp\left({\frac {ln\left({\frac {\eta -1}{\eta \gamma -1}}\right)}{\eta }}\right),\eta ,\gamma >1\\{\text{иначе мода отсутствует}}\end{cases}}$
Дисперсия	${\frac {2}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {2}{\eta }}\right)-{\frac {1}{\eta ^{2}}}\mathrm {B} ^{2}\left(\gamma +1,{\frac {1}{\eta }}\right)$

L-распределе́ние Сосновского — распределение случайной вещественной величины, принимающей значения из отрезка [0,1], характеризующееся указанной ниже функцией распределения. Данное распределение было предложено более 25 лет назад для анализа накопления усталостных повреждений при нерегулярном нагружении. За это время выяснилось, что (см., например), оно не является частным случаем никакого другого известного распределения и имеет важное значение в механике повреждений.

Определение

L-распределение определяется двухпараметрической интегральной функцией распределения:

$F(x)={\begin{cases}0,&x<0\\\left(1-\left(1-x\right)^{\eta }\right)^{\gamma },&0\leq x\leq 1\\1,&x>1\end{cases}}$

где η, γ – параметры формы (η > 0, γ > 0). Функция L-распределения вполне адекватно описывает процесс накопления повреждений в объекте и обладает всеми свойствами функций распределения непрерывных случайных величин.

Моменты случайной величины

Выражения моментов случайной величины ξ, подчиняющейся L-распределе­нию, могут быть представлены в явном виде лишь при определенных соотношениях значений параметров, не имеющих практической значимости. Однако они всегда могут быть выражены через Бета-функцию. Представим выражения для начальных моментов четырех младших порядков:

$\nu _{1}=M[\xi ]=1-{\frac {1}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {1}{\eta }}\right);$ $\nu _{2}=M[\xi ^{2}]=1-{\frac {2}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {1}{\eta }}\right)+{\frac {2}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {2}{\eta }}\right);$ $\nu _{3}=M[\xi ^{3}]=1-{\frac {3}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {1}{\eta }}\right)+{\frac {6}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {2}{\eta }}\right)-{\frac {3}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {3}{\eta }}\right);$

$\nu _{4}=M[\xi ^{4}]=1-{\frac {4}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {1}{\eta }}\right)+{\frac {12}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {2}{\eta }}\right)-{\frac {12}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {3}{\eta }}\right)+{\frac {4}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {4}{\eta }}\right).$

Центральные моменты L-распределе­нной случайной величины удобно определять через начальные моменты с помощью известных в теории вероятностей выражений:

$\mu _{1}=0;\mu _{2}=D[\xi ]=\nu _{2}-\nu _{1}^{2}={\frac {2}{\eta }}\mathrm {B} \left(\gamma +1,{\frac {2}{\eta }}\right)-{\frac {1}{\eta ^{2}}}\mathrm {B} ^{2}\left(\gamma +1,{\frac {1}{\eta }}\right).$

Характеристическая функция

Характеристическая функция L-распре­деления g(t), как и моменты, не выражается аналитически явно. Графики данной функции (для следующих значений параметров a) γ = 3; b) η = 1) представлены на рисунке.

Функция интенсивности отказов

Рассматривая L-распределенную случайную величину, как наработку объекта до отказа, функция интенсивности отказов объекта λ(x) имеет вид ($x\in [0,1]$, см. рисунок ниже)

$\lambda (x)={\frac {f(x)}{1-F(x)}}={\frac {\eta \gamma \left(1-\left(1-x\right)^{\eta }\right)^{\gamma -1}\left(1-x\right)^{\eta -1}}{1-\left(1-\left(1-x\right)^{\eta }\right)^{\gamma }}}$.

Функция интенсивности отказов для наработки, являющейся случайной величиной, подчиняющейся L-распределению

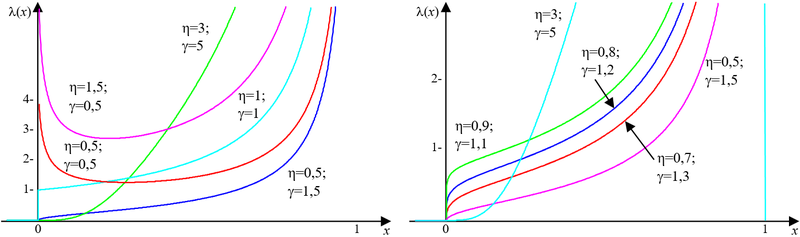
Функция интенсивности отказов монотонно возрастает при γ>1, поэтому L-распре­деление может использоваться в качестве адекватной модели постепенных (износовых) отказов объектов. При γ < 1 функция интенсивности отказов имеет U-образную форму, что позволяет использовать L-распре­деление для описания наработки объектов до отказа на всех этапах жизненного цикла объекта: в периоде приработки, нормальной эксплуатации и старения.

Оценивание параметров

Статистические оценки ${\hat {\eta }},{\hat {\gamma }}$  параметров L-распределения ${\eta },{\gamma }$ на практике предлагается определять как решение (численное) системы уравнений:

${\begin{cases}{\hat {M}}[\xi ]=1-{\frac {1}{\hat {\eta }}}\mathrm {B} \left({\hat {\gamma }}+1,{\frac {1}{\hat {\eta }}}\right)\\{\hat {D}}[\xi ]={\frac {2}{\hat {\eta }}}\mathrm {B} \left({\hat {\gamma }}+1,{\frac {2}{\hat {\eta }}}\right)-{\frac {1}{{\hat {\eta }}^{2}}}\mathrm {B} ^{2}\left({\hat {\gamma }}+1,{\frac {1}{\hat {\eta }}}\right)\end{cases}}$

где ${\hat {M}}[\xi ],{\hat {D}}[\xi ]$ – несмещенные и состоятельные оценки математического ожидания и дисперсии случайной величины ξ. Вопрос о существовании (возможно, единственности) решения системы уравнений, а также определение свойств полученных оценок (несмещенность, состоятельность, эффективность) представляет пока нерешенную, задачу.

Генерирование случайной величины

Генерирование случайной величины ξ, подчиняющейся L-распределению, целесообразно методом обратной функции с использованием реализаций R базовой случайной величины, равномерно распределенной на отрезке [0,1]:

$x=1-\left(1-R^{\frac {1}{\gamma }}\right)^{\frac {1}{\eta }}$.