Штрих Шеффера (Omjn] Oyssyjg)

Штрих Шеффера
И-НЕ, NAND
Диаграмма Венна
Определение	${\overline {x\cdot y}}$
Таблица истинности	$(1110)$
Логический вентиль
Нормальные формы
Дизъюнктивная	${\overline {x}}+{\overline {y}}$
Конъюнктивная	${\overline {x}}+{\overline {y}}$
Полином Жегалкина	$1\oplus xy$
Принадлежность предполным классам
Сохраняет 0	Нет
Сохраняет 1	Нет
Монотонна	Нет
Линейна	Нет
Самодвойственна	Нет

Штрих Ше́ффера (NAND, отрицание конъюнкции) — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Генри Шеффером в 1913 году.

Штрих Шеффера, обычно обозначаемый | или ↑, эквивалентен операции И-НЕ и задаётся в виде двумерной (двухаргументной, двухкоординатной) диаграммы (двумерного массива) из четырёх ячеек:

x↑y = x NAND y = NOT(x AND y) = !(x&&y)
y
1  0  
1  1 x

на которой сразу видно, что функция симметрична относительно главной диагонали, или таблицей истинности из трёх колонок (двенадцать ячеек):

X	Y	X | Y
0	0	1
0	1	1
1	0	1
1	1	0

Таким образом, высказывание X | Y означает, что X и Y несовместны, то есть не являются истинными одновременно. От перемены мест операндов результат операции не изменяется.

Инверсией штриха Шеффера является конъюнкция.

Штрих Шеффера, как и стрелка Пирса, образует базис для пространства булевых функций от двух переменных. То есть, используя только штрих Шеффера, можно построить все остальные операции. Например,

$X\,|\,X\equiv \neg X$ — отрицание;

$\left({X\,|\,X}\right)\,|\,\left({Y\,|\,Y}\right)\equiv X\vee Y$ — дизъюнкция;

$\left({X\,|\,Y}\right)\,|\,\left({X\,|\,Y}\right)\equiv X\wedge Y$ — конъюнкция;

$X\,|\,\left({Y\,|\,Y}\right)\equiv X\rightarrow Y$ — импликация.

Цифровая ТТЛ-микросхема SN7400N, содержащая в корпусе четыре элемента 2И-НЕ, реализующих функцию штрих Шеффера

В электронике это означает, что для реализации всего многообразия схем преобразования сигналов, представляющих логические значения, достаточно одного типового элемента. С другой стороны, такой подход увеличивает сложность реализующих логические выражения схем и тем самым снижает их надёжность. Примером может являться промышленная серия 74 (USA) (155 (СССР)).

Элемент 2И-НЕ (2-in NAND), реализующий штрих Шеффера, обозначается следующим образом (по стандартам ANSI):

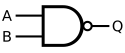
В европейских стандартах принято другое обозначение:

См. также

• Идентичность
• Отрицание
• Конъюнкция
• Дизъюнкция
• Эквиваленция
• Исключающее или
• Обратная импликация
• Таблица истинности

Литература

• Математический энциклопедический словарь. — М.: «Советская энциклопедия», 1988. — С. 639—639.
• Белоусов, Аркадий Алгебра логики и цифровые компьютеры