Универсальное свойство (Runfyjvgl,uky vfkwvmfk)

Во многих областях математики полезную конструкцию часто можно рассматривать как «наиболее эффективное решение» определенной проблемы. Определение универсального свойства использует язык теории категорий, чтобы сделать это определение точным и изучать его теоретическими методами.

В этой статье даётся общее описание универсального свойства. Чтобы лучше понять эту концепцию, будет полезно сначала изучить несколько примеров, которых существует довольно много: прямое произведение и копроизведение, свободная группа, группа Гротендика, компактификация Стоуна — Чеха, тензорное произведение, прямой предел и обратный предел, ядро и коядро, декартов квадрат и кодекартов квадрат, уравнитель и коуравнитель.

Мотивация

Прежде чем давать формальное определение, предложим некоторую мотивировку для изучения подобных конструкций.

Конкретное описание некоторой конструкции может быть длинным и беспорядочным, но если конструкция удовлетворяет универсальному свойству, можно смело забыть о деталях её описания; всё, что нужно для вывода её свойств, уже содержится в универсальном свойстве. Доказательства часто становятся более короткими и элегантными, если в них используется универсальное свойство, а не конкретные детали. Например, тензорную алгебру векторного пространства приходится строить в несколько шагов, тогда как с её универсальным свойством обращаться гораздо проще.
Универсального свойства достаточно, чтобы определить объект с точностью до изоморфизма. Таким образом, появляется ещё один способ доказать, что два объекта изоморфны, а именно доказать, что они обладают одинаковым универсальным свойством.
Универсальные свойства появляются всюду в математике. Изучив их абстрактные свойства, можно получить информацию обо всех подобных конструкциях и избежать повторения одного и того же анализа в каждом конкретном случае.

Формальное определение

Пусть U: D → C — функтор из категории D в категорию C, а X — объект категории C. Рассмотрим следующие двойственные определения:

Начальная (отталкивающая) стрелка из X в U — это начальный объект в категории морфизмов из X в U. Другими словами, это пара (A, φ), где A — это объект категории D и φ: X → U(A) — это морфизм в категории C, такой что выполняется следующее начальное свойство:

Для любого Y — объекта категории D и f: X → U(Y) — морфизма в категории C, существует единственный морфизм g: A → Y такой, что следующая диаграмма коммутативна:

Терминальная (притягивающая) стрелка из U в X — это терминальный объект в категории морфизмов из U в X. Другими словами, это пара (A, φ), где A — объект категории D и φ: U(A) → X — морфизм в категории C, такой что выполняется следующее терминальное свойство:

Для любого Y — объекта категории D и f: U(Y) → X — морфизма категории C, существует единственный морфизм g: Y → A, такой что следующая диаграмма коммутативна:

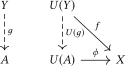
Термин универсальная стрелка означает «начальная либо терминальная стрелка», термин универсальное свойство означает «начальное либо терминальное свойство».

Примеры

Здесь будет приведено несколько примеров, иллюстрирующих общую идею. Читатель сможет сконструировать множество других примеров, прочитав статьи, цитировавшиеся во введении.

Тензорные алгебры

Пусть C — категория векторных пространств над полем K и D — категория ассоциативных алгебр над K. Рассмотрим забывающий функтор

U : K-Alg → K-Vect

сопоставляющий каждой алгебре подлежащее векторное пространство.

По произвольному объекту X из K-Vect — векторному пространству V — можно получить его тензорную алгебру T(V). А именно, она характеризуется следующим универсальным свойством:

«Любое линейное отображение из V в K-алгебру A может быть единственным образом продолжено до гомоморфизма алгебр T(V) → A.»

Это утверждение описывает начальное свойство тензорной алгебры, то есть тот факт, что пара (T(V), i), где i : V → T(V) — стандартное вложение, является начальной стрелкой из векторного пространства V в функтор U. Мы получили функтор T из K-Vect в K-Alg Это значит, что T является левым сопряженным функтором забывающего функтора U (см. раздел «связь с сопряжёнными функторами»).

Произведения

Произведение в теории категорий можно охарактеризовать его универсальным свойством. А именно: пусть X и Y — объекты категории D, а C — произведение категорий D × D. Определим диагональный функтор

Δ : D → D × D

как Δ(X) = (X, X) и Δ(f : X → Y) = (f, f). Тогда если (A, φ) — терминальная стрелка из Δ в (X, Y) — объект категории D × D, то A — объект категории D, называющийся прямым произведением X × Y, а φ — пара проекций

π₁ : X × Y → X

π₂ : X × Y → Y.

Свойства

Существование и единственность

Определение некоего свойства не гарантирует существование объекта, ему удовлетворяющего. Если однако, такой (A, φ) существует, то он единственен. Точнее говоря, он единственен с точностью до единственного изоморфизма. Проверим это для случая начальной стрелки: если (A′, φ′) — другая такая пара, то существует единственный изоморфизм k: A → A′ такой что φ′ = U(k)φ. Это легко увидеть, заменив (Y, f) из определения начального свойства на (A′, φ′).

Эквивалентные формулировки

Определение универсальной стрелки может быть перефразировано множеством способов. Пусть U — функтор из D в C, X — объект категории С. Тогда следующие формулировки эквивалентны:

(A, φ) — начальная стрелка из X в U
(A, φ) — начальный объект категории запятой (X ↓ U)
(A, φ) представляет функтор Hom_C(X, U—),

равно как и двойственные им формулировки.

Связь с сопряженными функторами

Пусть (A₁, φ₁) — начальная стрелка из X₁ в U и (A₂, φ₂) — начальная стрелка из X₂ в U. По начальному свойству любому морфизму h: X₁ → X₂ соответствует единственный морфизм g: A₁ → A₂, такой что следующая диаграмма коммутативна:

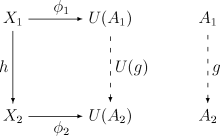
Если каждый объект X_i категории C допускает начальную стрелку в U, то соответствия $X_{i}\mapsto A_{i}$ и $h\mapsto g$ определяют функтор V из C в D. А отображения φ_i тогда определяют естественное преобразование из 1_C (тождественный функтор C) в UV. Функторы (V, U) образуют пару сопряженных функторов. Аналогичные утверждения верны в двойственной ситуации терминальных морфизмов из U, в этом случае (U, V) будут парой сопряженных функторов.

В действительности все пары сопряженных функторов получаются из конструкций такого вида. Пусть F: С → D и G: D → C — пара сопряжённых функторов с единицей η и коединицей ε (см. статью сопряженные функторы). Тогда существуют универсальные морфизмы для каждого объекта категорий C и D:

Для каждого объекта X из C, (F(X), η_X) — начальная стрелка из X в G. То есть для всех f: X → G(Y) существует единственный g: F(X) → Y, для которого следующие диаграммы коммутируют.
Для каждого объекта Y изD, (G(Y), ε_Y) — терминальная стрелка из F в Y. То есть для всех g: F(X) → Y существует единственный f: X → G(Y), для которого следующие диаграммы коммутируют.

Universal properties of a pair of adjoint functors

Универсальные конструкции являются более общими, чем конструкции сопряженных функторов: универсальная конструкция похожа на задачу оптимизации, и пара сопряжённых функторов определена, только если эта задача имеет решение для всех объектов категории.

История

Универсальные свойства многих топологических конструкций были описаны Пьером Самюэлем в 1948 году. Позднее они активно использовались Бурбаки. Тесно связанная с этим концепция сопряженных функторов была независимо предложена Даниэлем Каном в 1958 году.

Примечания

Литература

С. Маклейн Категории для работающего математика, — М.: ФИЗМАТЛИТ, 2004. — 352 с. — ISBN 5-9221-0400-4.
Paul Cohn, Universal Algebra (1981), D.Reidel Publishing, Holland. ISBN 90-277-1213-1.
Borceux, F. Handbook of Categorical Algebra: vol 1 Basic category theory (1994) Cambridge University Press, (Encyclopedia of Mathematics and its Applications) ISBN 0-521-44178-1