Теорема Вивиани (Mykjybg Fnfngun)

Теоре́ма Вивиа́ни — утверждение в геометрии треугольника, согласно которому сумма расстояний от произвольной точки внутри равностороннего треугольника до его сторон постоянна и равна высоте треугольника. Названа по имени итальянского математика Винченцо Вивиани.
В части постоянства суммы расстояний от произвольной внутренней точки до сторон утверждение может быть обобщено на равносторонние многоугольники и многоугольники с равными углами.
Доказательство
[править | править код]
Теорема может быть доказана путём сравнения площадей треугольников. Пусть — равносторонний треугольник, в котором — высота, — длина каждой из сторон. Точка выбирается произвольно внутри треугольника, и тогда , , — расстояния от точки до сторон треугольника. Тогда площадь можно определить следующим образом:
из чего вытекают следующие соотношения для площадей треугольников:
то есть:
Обратное утверждение также верно: если сумма расстояний от внутренней точки треугольника до сторон не зависит от положения этой точки, то треугольник равносторонний[1].
Обобщения
[править | править код]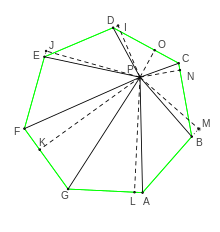
Многоугольники
[править | править код]Сумма длин перпендикуляров опущенных из произвольной внутренней точки на стороны правильного многоугольника, не зависит от положения точки и равна произведению длины апофемы на число сторон :
Это утверждение может быть доказано, аналогично равностороннему треугольнику, разбиением правильного многоугольника на треугольники. Если точка находится внутри -угольника с вершинами то отрезки делят многоугольник на треугольников с основаниями и площадь многоугольника равна сумме площадей всех треугольников. Так как основания малых треугольников одинаковы (это длина стороны -угольника), то сумма площадей равна произведению суммы высот на половину стороны. Площадь многоугольника и длина половины стороны не зависят от положения поэтому сумма высот треугольников также не зависит от положения [1].
Также справедливо утверждение, что сумма перпендикуляров, опущенных из произвольной внутренней точки на стороны параллелепипеда, а также на стороны равностороннего многоугольника или стороны многоугольника с равными углами не зависит от положения точки[2].
Необходимым и достаточным условием для того, чтобы произвольный выпуклый многоугольник имел постоянную сумму расстояний от любой внутренней точки до сторон, является существование трех неколлинеарных внутренних точек с равными суммами расстояний[3].
Многогранники
[править | править код]
Сумма расстояний от внутренней точки выпуклого многогранника до его граней постоянна, если все грани многогранника имеют одинаковую площадь[1]. Например, этим свойством обладают все тетраэдры с гранями одинаковой площади (то есть равногранные тетраэдры), а не только правильный тетраэдр[1].
Приложения
[править | править код]
ВПВ — верхний предел взрываемости;
НПВ — нижний предел взрываемости;
ПК — пороговая концентрация взрываемости.
Теорема Вивиани позволяет получать координаты точек на трёхкомпонентные диаграммы[англ.] путём проведения линий, параллельных сторонам равностороннего треугольника. В частности, таким образом можно строить диаграммы воспламеняемости[англ.].
В более общем случае, они позволяют таким же образом задавать координаты на правильном симплексе.
Примечания
[править | править код]- ↑ 1 2 3 4 Chen, Zhibo; Liang, Tian (2006). "The converse of Viviani's theorem". The College Mathematics Journal. 37 (5): 390—391. doi:10.2307/27646392. JSTOR 27646392.
- ↑ Elias Abboud «On Viviani’s Theorem and its Extensions» Архивная копия от 25 февраля 2018 на Wayback Machine pp. 2, 11
- ↑ Abboud, Elias (2017). "Loci of points inspired by Viviani's theorem". arXiv:1701.07339 [math.HO].
Ссылки
[править | править код]- Weisstein, Eric W. Viviani's Theorem (англ.) на сайте Wolfram MathWorld.
- Li Zhou, Viviani Polytopes and Fermat Points
- Viviani’s Theorem: What is it? at Cut the knot.
- Viviani’s Theorem by Jay Warendorff, the Wolfram Demonstrations Project.
- Viviani's theorem: Visualization + Proof на YouTube
















