Тензор напряжений (Myu[kj ughjx'yunw)

Те́нзор напряже́ний (иногда тензор напряжений Коши, тензор натяжений) — тензор второго ранга, описывающий механические напряжения в произвольной точке нагруженного тела, возникающих в этой точке при его (тела) малых деформациях. В случае объёмного тела, тензор часто записывается в виде матрицы 3×3:

{\boldsymbol {\sigma }}=\left[{\begin{matrix}\mathbf {T} ^{(\mathbf {e} _{1})}\\\mathbf {T} ^{(\mathbf {e} _{2})}\\\mathbf {T} ^{(\mathbf {e} _{3})}\\\end{matrix}}\right]=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\\\end{matrix}}\right]

а в случае двумерного тела (см. пример ниже) матрицей 2×2:

{\boldsymbol {\sigma }}=\left[{\begin{matrix}\mathbf {T} ^{(\mathbf {e} _{1})}\\\mathbf {T} ^{(\mathbf {e} _{2})}\\\end{matrix}}\right]=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}\\\sigma _{21}&\sigma _{22}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}\\\sigma _{yx}&\sigma _{yy}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\right]

где $\mathbf {T} ^{(e_{n})}$ — вектор механического напряжения, действующий на поверхность $e_{n}$ .

В случае матричной записи (в декартовой системе координат) величины $\sigma _{ij}$ (компоненты тензора напряжений), описывают напряжения испытываемые телом в какой-то заданной точке. В данной точке проводятся умозрительные плоскости с нормалями $\color {Red}e_{1}$ , $\color {Red}e_{2}$ , ... Нормальные компоненты сил, действующих на данные плоскости, записываются на главной диагонали $\sigma _{11}$ , $\sigma _{22}$ , ..., а в остальных позициях стоят касательные компоненты $\tau _{yx}$ , $\tau _{xy}$ , ... векторов напряжений на этих плоскостях.

В случае больших деформаций (конечные деформации), приходится использовать такие подходы как тензор напряжений Пиолы — Кирхгофа, тензор Биота или тензор напряжения Кирхгофа.

Физический смысл тензора напряжений на примере в двумерном случае

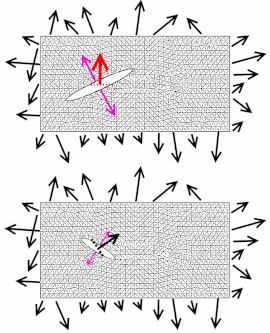
Простейшей иллюстрацией, позволяющей понять физический смысл тензора напряжений, будет, вероятно, не рассмотрение случая напряжения в некотором объёмном теле, а, наоборот, рассмотрение напряжения в плоском двумерном теле. Для этого рассмотрим напряжение отрезка ткани под внешней нагрузкой (см. рис. А).

На рисунке изображен прямоугольный кусок ткани под внешней нагрузкой, которая изображена чёрными стрелками по периметру прямоугольника. В данном случае нагрузкой может служить растяжение её руками в разные стороны, или натягивание ткани на какую-то сложную форму.

Интуитивно понятно, что из-за формы, ориентации молекул, атомных слоёв и разного плетения волокон (на рис.А расположение волокон схематично изображено мелкой серой сеткой) в разных точках ткани напряжение будет разным: где-то будут области, которые подвергаются вертикальному растяжению, а в других областях волокна будут испытывать напряжение сдвига.

Каждой точке на поверхности отрезка ткани соответствует своё уникальное значение $\mathbf {T}$ напряжения. Это значит, что каждой точке $(x_{0},y_{0})$ ткани соответствует свой математический объект — $\mathbf {T}$ — тензор второго ранга.

Чтобы понять, как тензор $\mathbf {T}$ показывает состояние напряжения в какой-нибудь точке ткани, можно сделать маленький разрез в данной точке и понаблюдать, в каком направлении будут расходиться данные разрезы. Так, на рис. А мы сделали два разреза в разных точках ткани: направление одного разреза $\color {red}c$ показано красной пунктирной линией, направление другого $\color {blue}c$ — синей пунктирной линией. Чтобы математически описать направление данных разрезов, используется вектор нормали (вектор, перпендикулярный плоскости разреза). Так, у разреза $\color {red}c$ вектор нормали $\color {red}{\vec {c}}$ красный и направлен перпендикулярно плоскости разреза, у разреза $\color {blue}c$ ситуация похожая. Направление роста разрыва в ткани обозначено фиолетовыми векторами $\color {RedViolet}{\vec {t}}$ .

Для предсказания того, куда будет развиваться разрез, как раз и используется тензор напряжений. Математически данное предсказание выглядело бы так:

Определить «тензорную функцию» $f(x,y)=\mathbf {T_{x,y}} ,$ аргументами которой являются координаты точек внутри тела, а значением является тензор, описывающий состояние напряжения в заданной точке тела.
Выбрать точку в теле, например, $(x_{0},y_{0}),$ и из $f(x,y)$ получить тензор, который описывает состояние напряжения в точке $\mathbf {T_{x_{0},y_{0}}} .$
Определить направление плоскости $\color {red}{\vec {c}}$ , в которой будет проводиться разрез тела.
Умножить направление разреза $\color {red}{\vec {c}}$ в точке $(x_{0},y_{0})$ на тензор напряжения в данной точке $\mathbf {T_{x_{0},y_{0}}}$ , что в математической записи выглядит как ${\mathbf {T_{x_{0},y_{0}}} \color {red}{\vec {c}}}=\color {RedViolet}{\vec {t}}.$
Вектор $\color {RedViolet}{\vec {t}}$ и покажет, куда будет распространяться разрез $\color {red}{\vec {c}}$ в точке $(x_{0},y_{0})$ .

Разрезы $\color {red}{\vec {c}}$ и $\color {blue}{\vec {c}}$ — это вектора, а напряжение в точке $\mathbf {T}$ — это тензор.

Следует понимать, что разнонаправленные разрезы, совершённые в одной и той же точке тела, повлекут за собой различный отклик ткани. Данное явление показано на рис. Б, где разрастание разрыва ткани происходит по разным направлениям $\color {RedViolet}{\vec {t}}$ и с разной интенсивностью $||{\color {RedViolet}{\vec {t}}}||$ , в ответ на различные направления первоначальных разрезов $\color {red}{\vec {c}}$ и ${\vec {c}}$ , совершённых в одной и той же точке.

Как раз для описания такого сложного поведения и используются тензоры, которые в данном случае служат векторными функциями $f_{x_{0},y_{0}}({\vec {c}})=\mathbf {T_{x_{0},y_{0}}} {\vec {c}}={\vec {t}}$ , определёнными в каждой точке $(x_{0},y_{0})$ куска ткани, которые ставят все возможные направления ${\vec {c}}$ разрезов в соответствие со всеми возможными направлениями ${\vec {t}}$ дальнейшего разрыва ткани.

Вывод компонентов тензора

Компоненты тензора напряжений $\sigma _{ij}$ в декартовой системе координат $Ox_{i}$ (то есть $Oxyz$ ) вводят следующим образом. Рассматривают бесконечно малый объём тела (сплошной среды) в виде прямоугольного параллелепипеда, грани которого ортогональны координатным осям и имеют площади $dS_{i}$ . На каждой грани $dS_{i}$ параллелепипеда действуют поверхностные силы $dF_{i}$ . Если обозначить проекции этих сил на оси $Ox_{j}$ как $dF_{ij}$ , то компонентами тензора напряжений называют отношение проекций силы к величине площади грани, на которой действует эта сила:

\sigma _{ij}={\frac {dF_{ij}}{dS_{i}}}

По индексу $i$ здесь суммирования нет. Компоненты $\sigma _{11}$ , $\sigma _{22}$ , $\sigma _{33}$ , обозначаемые также как $\sigma _{xx}$ , $\sigma _{yy}$ , $\sigma _{zz}$ — это нормальные напряжения, они представляют собой отношение проекции силы $dF_{i}$ на нормаль к площади рассматриваемой грани $dS_{i}$ :

\sigma _{11}={\frac {dF_{11}}{dS_{1}}}

и т. д.

Компоненты $\sigma _{12}$ , $\sigma _{23}$ , $\sigma _{31}$ , обозначаемые также как $\tau _{xy}$ , $\tau _{yz}$ , $\tau _{zx}$ — это касательные напряжения, они представляют собой отношение проекции силы $dF_{i}$ на касательные направления к площади рассматриваемой грани $dS_{i}$ :

\sigma _{12}={\frac {dF_{12}}{dS_{1}}}

и т. д.

При отсутствии собственного момента импульса сплошной среды, а также объёмных и поверхностных пар тензор напряжений симметричен (так называемый закон парности касательных напряжений), что является следствием уравнения баланса момента импульса. В частности, тензор напряжений симметричен в классической теории упругости и в гидродинамике идеальной и линейно-вязкой жидкостей.

Тензор напряжений в релятивистской физике

С точки зрения теории относительности, компоненты тензора напряжений являются девятью пространственными компонентами тензора энергии-импульса.

Тензор напряжений в классической электродинамике

В классической электродинамике тензор напряжений электромагнитного поля (максвелловский тензор напряжений^[1], тензор натяжений Максвелла^[2]) в Международной системе единиц (СИ) имеет вид:

T_{ij}=E_{i}D_{j}+B_{i}H_{j}-{\frac {1}{2}}\delta _{ij}(\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} )=E_{i}D_{j}+B_{i}H_{j}-\delta _{ij}W,

где $W$ — плотность энергии электромагнитного поля.

См. также

Примечания

↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 115. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
↑ Степановский Ю. П. Максвелла тензор натяжений // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 32—33. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.

Литература

Седов Л. И. Механика сплошной среды. Том 1. М.: Наука, 1970. 492 c.
Трусделл К. Первоначальный курс рациональной механики сплошных сред. М.: Наука, 1975. 592 с.
Димитриенко Ю. И. Нелинейная механика сплошной среды. М.: Физматлит, 2010.

[1] Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 115. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.

[2] Степановский Ю. П. Максвелла тензор натяжений // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 32—33. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.

[1]

[2]