Список кубик классификации Ньютона (Vhnvkt trQnt tlgvvnsntgenn U,Zmkug)

Основная статья: Классификации кубик Ньютона

Следующие таблицы — списки 78 кубик первой классификации Ньютона.

Класс I. Гиперболическая гипербола

Здесь описан класс I гиперболических гипербол, $a>0.$ (англ. Class I. Redundant Hyperbolas).

Гиперболическая гипербола

$xy^{2}+ey=ax^{3}+bx^{2}+cx+d,\quad$ $a>0,$

имеет три обыкновенные асимптоты

$x=0,\quad$ $y=\pm {\sqrt {a}}\left(x+{\frac {b}{2a}}\right),$

пересекающиеся в вершинах следующего асимптотического треугольника:

$\left(0,\;{\frac {b}{2{\sqrt {a}}}}\right),$ $\left(0,\;-{\frac {b}{2{\sqrt {a}}}}\right),$ $\left(-{\frac {b}{2a}},\;0\right).$

Гиперболическая гипербола пересекает три свои асимптоты на конечном расстоянии в следующих трёх точках (у Смогоржевского и Столовой опечатка: в ординате не хватает множителя $\mp {\sqrt {a}}$), лежащих на одной прямой:

$\left(0,\;{\frac {d}{e}}\right),\;\left({\frac {4ad\pm 2be{\sqrt {a}}}{b^{2}-4ac\mp 4ae{\sqrt {a}}}},\;\mp {\sqrt {a}}{\frac {8a^{2}d+b^{3}-4abc}{2a(b^{2}-4ac\mp 4ae{\sqrt {a}})}}\right).$

Род 1. Адиаметралъная гиперболическая гипербола

Здесь представлена таблица со списком рода 1 адиаметралъных гиперболических гипербол, $e\neq 0$. Будем также полагать, что $b\neq 0$ (англ. Genus 1. Adiametral Redundant Hyperbolas).

Адиаметралъная гиперболическая гипербола (без диаметров) имеет характеристическое уравнение

$ax^{4}+bx^{3}+cx^{2}+dx+{\frac {1}{4}}e^{2}=0,\quad$ $e\neq 0,$

а также $b\neq 0,$ и пусть $x_{1},\;x_{2},\;x_{3},\;x_{4}$ — его корни.

Рассматривая уравнение гиперболической гиперболы как квадратное относительно $y,$ получаем:

$y={\frac {-e\pm 2{\sqrt {ax^{4}+bx^{3}+cx^{2}+dx+{\frac {1}{4}}e^{2}}}}{2x}}=$

$={\frac {-e\pm 2{\sqrt {a(x-x_{1})(x-x_{2})(x-x_{3})(x-x_{4})}}}{2x}},$

где действительное или мнимое значение переменной $y$ определяет знак подкоренного выражения, то есть знак левой части уравнения гиперболической гиперболы.

Отметим следующую гиперболу и её свойства:

$y=-{\frac {e}{2x}}:$

• эта гипербола делит пополам каждую хорду адиаметралъной гиперболической гиперболы, перпендикулярную к оси абсцисс;
• эта гипербола пересекает адиаметралъную гиперболическу гиперболу в следующих точках и только в них:

$(x_{1},\;-{\frac {e}{2x_{1}}}),(x_{2},\;-{\frac {e}{2x_{2}}}),(x_{3},\;-{\frac {e}{2x_{3}}}),(x_{4},\;-{\frac {e}{2x_{3}}}).$

Существует девять разных адиаметралъных гиперболических гипербол, описанных в следующей таблице.

Адиаметралъные гиперболические гиперболы, $e\neq 0$, $b\neq 0$

№	Описание	Изображение, $e>0$
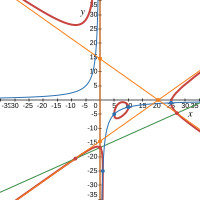
1	1. Все корни характеристического уравнения — различные действительные одного знака, например, $0<x_{1}<x_{2}<x_{3}<x_{4}$ На графике овал находится внутри асимптотического треугольника.
2	2. Все корни характеристического уравнения — действительные и различные, два положительны, два отрицательны, например, $x_{1}<x_{2}<0<x_{3}<x_{4}.$
3	3. Все корни характеристического уравнения — действительные, два равны и больше или меньше остальных разных корней с другим знаком, например, $x_{1}=x_{2}<0<x_{3}<x_{4}.$
4	4. Все корни характеристического уравнения — действительные одного знака, два равны и больше или меньше остальных разных корней, например, $0<x_{1}<x_{2}<x_{3}=x_{4}.$ На графике точка самопересечения лежит внутри асимптотического треугольника.
5	5. Все корни характеристического уравнения — действительные одного знака, два равны и больше одного и меньше другого остальных разных корней, например, $0<x_{1}<x_{2}=x_{3}<x_{4}.$ На графике изолированная точка $\left(x_{2},-{\frac {e}{2x_{2}}}\right)$ лежит внутри асимптотического треугольника.
6	6. Все корни характеристического уравнения — действительные, три равны, например, $x_{1}=x_{2}=x_{3}<x_{4}.$ На графике касп $\left(x_{1},-{\frac {e}{2x_{1}}}\right)$ лежит внутри асимптотического треугольника.
7	7. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}>x_{2},\;x_{3,\;4}=\alpha \pm \beta i.$ Имеем: $y={\frac {-e\pm 2{\sqrt {a(x-x_{1})(x-x_{2})((x-\alpha )^{2}+\beta ^{2})}}}{2x}}.$
8	8. Два корня характеристического уравнения — равные действительные, два комплексно сопряжённых, например, $x_{1}=x_{2},\;x_{3,\;4}=\alpha \pm \beta i.$
9	9. Все корни характеристического уравнения — комплексные попарно сопряжённые, например, $x_{1,\;2}=\alpha _{1}\pm \beta _{1}i,\;x_{3,\;4}=\alpha _{2}\pm \beta _{2}i.$

Род 2. Монодиаметралъная гиперболическая гипербола

Здесь представлена таблица со списком рода 2 монодиаметралъных гиперболических гипербол, $e=0$, $b\neq 0$, $b^{2}\neq 4ac$ (англ. Genus 2. Monodiametral Redundant Hyperbolas).

Монодиаметралъная гиперболическая гипербола имеет один диаметр

$y=0$

и характеристическое уравнение

$ax^{4}+bx^{3}+cx^{2}+dx=0,\quad$ $b\neq 0,\quad$ $b^{2}\neq 4ac$

и пусть $x_{1},\;x_{2},\;x_{3},\;x_{4}$ — его корни.

Ньютон относит к этому роду двенадцать разных монодиаметралъных гиперболических гипербол, описанных в следующей таблице.

Монодиаметралъные гиперболические гиперболы, $b\neq 0,$ $b^{2}\neq 4ac$

№	Описание	Изображение, $b<0$
10	1. Все корни характеристического уравнения — различные действительные одного знака, например, $x_{1}=0<x_{2}<x_{3}<x_{4}.$ На графике овал находится внутри асимптотического треугольника.
11	2. Все корни характеристического уравнения — различные действительные разных знаков и $|x_{1}|>x_{3}+x_{4},$ например, $x_{1}<x_{2}=0<x_{3}<x_{4}.$
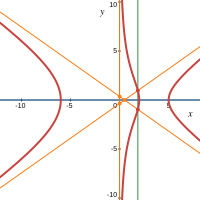
12	3. Все корни характеристического уравнения — различные действительные разных знаков и $|x_{1}|<x_{3}+x_{4},$ например, $x_{1}<x_{2}=0<x_{3}<x_{4}.$
13	4. Два отрицательных корня характеристического уравнения равны, меньше различных неотрицательных и $|x_{1}|>0{,}5x_{4},$ например, $x_{1}=x_{2}<x_{3}=0<x_{4}.$
14	5. Два отрицательных корня характеристического уравнения равны, меньше различных неотрицательных и $|x_{1}|<0{,}5x_{4},$ например, $x_{1}=x_{2}<x_{3}=0<x_{4}.$
15	6. Все корни характеристического уравнения — действительные одного знака, кратный корень больше третьего и меньше четвёртого, например, $x_{1}=0<x_{2}=x_{3}<x_{4}.$ На графике изолированная точка $(x_{2},\;0)$ лежит внутри асимптотического треугольника.
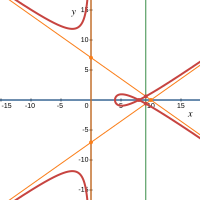
16	7. Все корни характеристического уравнения — действительные одного знака, кратный корень больше разных остальных, например, $x_{1}=0<x_{2}<x_{3}=x_{4}.$ На графике точка самопересечения $(x_{3},\;0)$ лежит внутри асимптотического треугольника.
17	8. Все корни характеристического уравнения — действительные, три равны, например, $x_{1}=0<x_{2}=x_{3}=x_{4}.$ На графике касп $(x_{2},0)$ лежит внутри асимптотического треугольника.
18	9. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}=0>x_{2},\;x_{3,\;4}=\alpha \pm \beta i,$ $x_{2}$ и $\alpha$ одинаковых знаков, причём $|x_{2}|\leqslant 2|\alpha |.$ Имеем: $y={\frac {\pm 2{\sqrt {a(x-x_{1})(x-x_{2})((x-\alpha )^{2}+\beta ^{2})}}}{2x}}.$
19	10. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}=0>x_{2},\;x_{3,\;4}=\alpha \pm \beta i,$ $x_{2}$ и $\alpha$ одинаковых знаков, причём $|x_{2}|>2|\alpha |.$
20	11. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}=0>x_{2},\;x_{3,\;4}=\alpha \pm \beta i,$ $x_{2}$ и $\alpha$ разных знаков, причём $|x_{2}|<2|\alpha |$ и $x_{2}(x_{2}-4\alpha )<4\beta ^{2}.$ При $|x_{2}|=2|\alpha |$ имеем $b=0$, то есть гиперболическая гипербола имеет род 4.
21	12. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}=0>x_{2},\;x_{3,\;4}=\alpha \pm \beta i,$ $x_{2}$ и $\alpha$ разных знаков, причём $|x_{2}|<2|\alpha |$ и $x_{2}(x_{2}-4\alpha )>4\beta ^{2}.$

Род 3. Тридиаметралъная гиперболическая гипербола

Здесь представлена таблица со списком рода 3 тридиаметралъных гиперболических гипербол, $e=0$, $b^{2}=4ac$ (англ. Genus 3. Tridiametral Redundant Hyperbolas).

Тридиаметралъная гиперболическая гипербола при $b=-2{\sqrt {ac}}$ имеет три диаметра

$y=0,\quad$ $y=-3x{\sqrt {a}}+{\sqrt {c}},\quad$ $y=3x{\sqrt {a}}-{\sqrt {c}}$

и характеристическое уравнение

$ax^{4}+bx^{3}+cx^{2}+dx=0,\quad$ $b^{2}=4ac,$

и пусть $x_{1},\;x_{2},\;x_{3},\;x_{4}$ — его корни.

Это характеристическое уравнение имеет комплексные корни. Пусть $x_{1}=r\neq 0,\;$ $x_{2,4}=\alpha \pm \beta i,\;$ $x_{4}=0.$ В этих условиях получаем следующее уравнение гиперболической гиперболы:

$xy^{2}=a(x^{3}-(2\alpha +r)x^{2}+(\alpha ^{2}+\beta ^{2}+2\alpha r)x-(\alpha ^{2}+\beta ^{2})r).$

Перепишем условие $b^{2}=4ac:$

$(2\alpha +r)^{2}=4(\alpha ^{2}+\beta ^{2}+2\alpha r),\quad$$r^{2}-4\alpha r-4\beta ^{2}=0.$

откуда получаем следующее выражение для $r$, решая квадратное уравнение:

$r=2(\alpha \pm {\sqrt {\alpha ^{2}+\beta ^{2}}}).$

Ньютон относит к этому роду два вида разных тридиаметралъных гиперболических гипербол, описанных в следующей таблице. Для первого вида переменные $r$ и $a$ имеют одинаковые знаки, для второго — разные.

Тридиаметралъные гиперболические гиперболы, $b^{2}=4ac$

№	Описание	Изображение, $\alpha >0$
22	1. Например, корни характеристического уравнения — $x_{1}=2(\alpha +{\sqrt {\alpha ^{2}+\beta ^{2}}}),\;$ $x_{2,4}=\alpha \pm \beta i,\;$ $x_{4}=0,$ где $\alpha >0.$
23	2. Например, корни характеристического уравнения — $x_{1}=2(\alpha -{\sqrt {\alpha ^{2}+\beta ^{2}}}),\;$ $x_{2,4}=\alpha \pm \beta i,\;$ $x_{4}=0,$ где $\alpha >0.$

Род 4. Гиперболическая гипербола с асимптотами, пересекающимися в одной точке

Здесь представлена таблица со списком рода 4 гиперболических гипербол с асимптотами, пересекающимися в одной точке, $b=0$ (англ. Genus 1. Redundant Hyperbolas with asymptotes concurrent). Эти кривые получаются стягиванием в точку асимптотического треугольника у адиаметралъных, монодиаметралъных и тридиаметральны гиперболических гипербол, всего девять случаев.

Гиперболические гиперболы с асимптотами, пересекающимися в одной точке, $b=0$

№	Описание	Изображение
Адиаметралъные гиперболические гиперболы, $e\neq 0$
24	1. Получается из типа 7 рода 1. Все корни характеристического уравнения — разные, два действительных, два комплексно сопряжённых, например, $x_{1}>x_{2},\;x_{3,\;4}=\alpha \pm \beta i.$ Имеем: $y={\frac {-e\pm 2{\sqrt {a(x-x_{1})(x-x_{2})((x-\alpha )^{2}+\beta ^{2})}}}{2x}}.$
25	2. Получается из типа 3 (или 8) рода 1. Все корни характеристического уравнения — действительные, два равны и больше или меньше остальных разных корней с другим знаком, например, $x_{1}=x_{2}<0<x_{3}<x_{4}.$
26	3. Получается из типа 2 (или 9) рода 1. Все корни характеристического уравнения — действительные и различные, два положительны, два отрицательны, например, $x_{1}<x_{2}<0<x_{3}<x_{4}.$ График адиаметралъной гиперболической гиперболы не проходит через точку пересечения асимптот.
27	4. Получается из типа 2 (или 9) рода 1. Все корни характеристического уравнения — действительные и различные, два положительны, два отрицательны, например, $x_{1}<x_{2}<0<x_{3}<x_{4}.$ График адиаметралъной гиперболической гиперболы проходит через точку пересечения асимптот.
Монодиаметралъные гиперболические гиперболы, $e=0,$ $c\neq 0$
Тридиаметралъные гиперболические гиперболы, $e=c=0$

Источники

• Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка. М.: Физматлит, 1961. 271 с., ил.
• Ball W. W. Rouse Newton's classification of cubic curves, Proc. London Math. Soc. 1891. Vol. 50, Iss. 2. P. 35–40.