Редко используемые тригонометрические функции (Jy;tk nvhkl,[rybdy mjnikukbymjncyvtny srutenn)

Редко используемые тригонометрические функции — функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом, секансом и косекансом). К ним относятся:

Определение тригонометрических функций через окружность. Отрезки CD и DE описывают соответственно версинус и эксеканс.

Графики функций versin, vercos, haversin, havercos, exsec, excsc

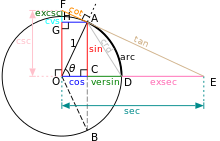
• Синус-верзус (другие написания: версинус, синус версус, называется также «стрелка дуги»). Определяется как $\operatorname {versin} \,\vartheta =1-\cos \vartheta =2\sin ^{2}{\frac {\vartheta }{2}}.$ Представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Иногда используются обозначения $\operatorname {vers} \,\vartheta ,\quad \sin \,\operatorname {vers} \,\vartheta .$
• Косинус-верзус (другие написания: косинус версус или веркосинус). Определяется как $\operatorname {vercos} \,\vartheta =\operatorname {versin} \,\left({\frac {\pi }{2}}-\vartheta \right)=1+\cos \vartheta .$Иногда используются обозначения cos vers.
• Аккорд — одна из редких тригонометрических функций, которая использовалась в ранней тригонометрии. Определяется эта функция как 2sin(x/2).
• Коверсинус (лат. coversinus, сокращение от coversed sine. Другие написания: синус-коверзус, покрытый синус.) Определяется эта функция как $\operatorname {coversin} \,\vartheta =1-\sin \vartheta$. Для этой функции используются также обозначения $\operatorname {covers} \,\vartheta$ или $\operatorname {cvs} \,\vartheta$.
• Коверкосинус (лат. covercosinus, сокращение от covercosed sinе. Другие написания: косинус-коверзус, покрытый косинус.) Определяется функция как $\operatorname {covercos} \,\vartheta =1+\sin \vartheta$. Для данной функции также используeтся обозначениe $\operatorname {cvc} \,\vartheta$.
• Гаковерсинус (лат. hacoversinus, coкращение от half the coversed sine.) Определяется данная функция как $\operatorname {hacoversin} \,\vartheta ={\frac {\operatorname {coversin} \,\vartheta }{2}}$.
• Гаковеркосинус (лат. hacovercosinus, сокращение от half the covercosed sine.) Определяется как $\operatorname {hacovercos} \,\vartheta ={\frac {\operatorname {covercos} \,\vartheta }{2}}$.
• Гаверсинус (лат. haversinus, сокращение от half the versed sine). Определяется как $\operatorname {haversin} \,\vartheta ={\frac {\operatorname {versin} \,\vartheta }{2}}=\sin ^{2}{\frac {\vartheta }{2}}.$ Используется также обозначение $\operatorname {hav} \,\vartheta .$
• Гаверкосинус (лат. havercosinus, сокращение от half the versed cosine). Определяется как $\operatorname {havercos} \,\vartheta ={\frac {\operatorname {vercos} \,\vartheta }{2}}=\cos ^{2}{\frac {\vartheta }{2}}.$ Используется также обозначение $\operatorname {hac} \,\vartheta .$
• Эксеканс (лат. exsecant) или экссеканс. Определяется как $\operatorname {exsec} \,\vartheta =\sec \vartheta -1.$
• Экскосеканс — дополнительная функция к эксекансу: $\operatorname {excsc} \,\vartheta =\operatorname {exsec} \,\left({\frac {\pi }{2}}-\vartheta \right)=\operatorname {cosec} \,\vartheta -1.$

Использование

Версинус, коверсинус и гаверсинус были удобны для ручных расчётов с использованием логарифмов (использовали логарифмы или логарифмическую линейку), поскольку они всюду неотрицательны, однако в связи с развитием вычислительных средств эта область применения неактуальна. В настоящее время эти функции используются для описания соответствующих сигналов в электронике (например, в функциональных генераторах). Гаверсинус также используется в навигационных расчётах для избежания ошибок округления в вычислительных системах с ограниченной разрядностью. Гаверсинус используется в формуле Хаверсина также для навигационных расчётах.

Функция эксеканс использовалась в железнодорожном строительстве, сферической тригонометрии, а также в геодезии вплоть до 1980-х годов. Экскосеканс использовался в кинетической энергии фермионов знаменитым физиком Альбертом Эйнштейном.

Синус-верзус

Основная статья: Синус-верзус

Определение

Синус-верзус определён через синус и косинус как

$\operatorname {versin} \,\vartheta =1-\cos \vartheta =2\sin ^{2}\left({\frac {\vartheta }{2}}\right).$

Синус-верзус вместе с косинусом составляет радиус окружности.

Свойства

Версинус — периодическая функция с периодом $2\pi$. Версинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.

$\operatorname {versin}$ можно использовать в плоскости комплексных чисел.

Производная версинуса

${\frac {d}{dz}}\operatorname {versin} \ z=\operatorname {sin} \ z$

Первообразная версинуса

$\int \operatorname {versin} \,z\,dz=z-\sin z+C$

Косинус-верзус

Определение

Косинус-верзус определён через версинус и косинус как

$\operatorname {vercos} \,\vartheta =\operatorname {versin} \,\left({\frac {\pi }{2}}-\vartheta \right)=1+\cos \vartheta .$

Свойства

Веркосинус — периодическая функция с периодом $2\pi$. Веркосинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.

$\operatorname {vercos}$ можно использовать в плоскости комплексных чисел.

Производная веркосинуса

${\frac {d}{dz}}\operatorname {vercos} \ z=-\sin \ z$

Первообразная веркосинуса

$\int \operatorname {vercos} \,z\,dz=z+\sin z+C$

Гаверсинус

Определение

Гаверсинус определён через верзус-синус и синус как

$\operatorname {haversin} \,\vartheta ={\frac {\operatorname {versin} \,\vartheta }{2}}=\sin ^{2}{\frac {\vartheta }{2}}.$

Свойства

Гаверсинус — периодическая функция с периодом $2\pi$. Гаверсинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.

$\operatorname {haversin}$ можно использовать в плоскости комплексных чисел.

Производная гаверсинуса

${\frac {d}{dz}}\operatorname {haversin} \ z={\frac {\operatorname {sin} \ z}{2}}$

Первообразная гаверсинуса

$\int \operatorname {haversin} \,z\,dz=-{\frac {\operatorname {sin} \ z}{2}}+{\frac {z}{2}}+C$

Гаверкосинус

Определение

Гаверкосинус определён через верзус-косинус и косинус как

$\operatorname {havercos} \,\vartheta ={\frac {\operatorname {vercos} \,\vartheta }{2}}=\cos ^{2}{\frac {\vartheta }{2}}.$

Свойства

Гаверкосинус — периодическая функция с периодом $2\pi$. Гаверкосинус определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.

$\operatorname {havercos}$ можно использовать в плоскости комплексных чисел.

Производная гаверкосинуса

${\frac {d}{dz}}\operatorname {havercos} \ z=-{\frac {\operatorname {cos} \ z}{2}}$

Первообразная гаверкосинуса

$\int \operatorname {havercos} \,z\,dz={\frac {\operatorname {cos} \,z}{2}}+{\frac {z}{2}}+C$

Эксеканс

Определение

Эксеканс определён через секанс как

$\operatorname {exsec} \,\vartheta =\sec \vartheta -1.$

Эксеканс можно определить через тангенс и синус-верзус как

exsec(x) = versin(x)/cos(x)

exsec(x) = tg(x)*tg(x/2)

Свойства

Эксеканс — периодическая функция с периодом $2\pi$. Эксеканс определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.

$\operatorname {exsec}$ можно использовать в плоскости комплексных чисел.

Производная эксеканса

${\frac {d}{dz}}\operatorname {exsec} \ z=\operatorname {tg} \ z\cdot \operatorname {sec} \ z$

Первообразная эксеканса

$\int \operatorname {exsec} (z)\,\mathrm {d} z=\ln \left[\cos \left({\frac {z}{2}}\right)+\sin \left({\frac {z}{2}}\right)\right]-\ln \left[\cos \left({\frac {z}{2}}\right)-\sin \left({\frac {z}{2}}\right)\right]-z+C$

Экскосеканс

Определение

Экскосеканс определён через эксеканс и косеканс как

$\operatorname {excsc} \,\vartheta =\operatorname {exsec} \,\left({\frac {\pi }{2}}-\vartheta \right)=\operatorname {cosec} \,\vartheta -1.$

Свойства

Экскосеканс — периодическая функция с периодом $2\pi$. Экскосеканс определён, непрерывен и бесконечно дифференцируем для всех действительных чисел.

$\operatorname {excsc}$ можно использовать в плоскости комплексных чисел.

Производная экскосеканса

${\frac {d}{dz}}\operatorname {excsc} \ z=-\operatorname {ctg} \ z\cdot \operatorname {sec} \ z$

Первообразная экскосеканса

$\int \operatorname {excsc} (z)\,\mathrm {d} z=\ln \left[\tan \left({\frac {z}{2}}\right)\right]-z+C$

Ссылки

• Статьи в энциклопедии Mathworld, описывающие эксеканс, версинус, коверсинус, гаверсинус, гаверкосинус.
• Вычисление расстояния и начального азимута между двумя точками на сфере.
• Вычисление расстояния между двумя точками на сфере: использование гаверсинуса в sql.

См. также

• Интегральный синус
• Интегральный косинус
• Многочлены Чебышёва
• Функция Гудермана