Подпись Лэмпорта (Hk;hnv, Lzbhkjmg)

Подпись Лэмпорта (англ. Lamport signature) — это криптосистема цифровой подписи с открытым ключом. Может быть построена на любой односторонней функции. Была предложена в 1979 году и названа в честь её автора, американского учёного, Лесли Лэмпорта.

Описание

Пусть у Алисы есть 256-битная криптографическая хеш-функция и криптографически стойкий генератор псевдослучайных чисел. Она хочет создать и использовать пару ключей Лэмпорта — секретный ключ и соответствующий ему открытый ключ.

Создание пары ключей

Чтобы создать секретный ключ, Алиса использует генератор случайных чисел для получения 256 пар случайных чисел (всего 2×256 чисел). Каждое число состоит из 256 бит, то есть общий размер равен 2×256×256 бит = 16 КиБ. Эти числа будут секретным ключом Алисы, и она будет хранить их в секретном месте, чтобы использовать в дальнейшем.

Чтобы создать открытый ключ, Алиса хеширует каждое из 512 чисел секретного ключа, таким образом получая 512 хешей по 256 бит каждый. Эти 512 хешей составляют открытый ключ Алисы, который она публикует.

Подпись сообщения

Теперь Алиса хочет подписать сообщение. Для начала она хеширует сообщение и получает 256-битный хеш. Затем, для каждого бита в этом хеше, она берёт соответствующее число из секретного ключа. Если, например, первый бит в хеше сообщения равен нулю, она берёт первое число из первой пары секретного ключа. Если же первый бит равен единице, она использует второе число из первой пары. И так далее. В итоге получается 256 случайных чисел, размер которых составляет 256×256 бит = 8 КиБ. Эти числа и составляют подпись, которую Алиса отправляет вместе с сообщением.

Стоит обратить внимание, что после того как Алиса использовала свой секретный ключ, он никогда не должен быть использован снова. Остальные 256 чисел, которые она не использовала в подписи, Алиса никогда не должна публиковать или использовать. Предпочтительно, чтобы она их удалила, так как иначе кто-то может получить к ним доступ и сгенерировать с их помощью поддельную подпись.

Проверка подписи

Боб хочет проверить подпись Алисы для сообщения. Он также хеширует сообщение и получает 256-битный хеш. Затем для каждого бита в этом хеше он выбирает число из открытого ключа Алисы. Эти числа выбираются по такому же принципу, по какому Алиса выбирала числа для составления подписи. То есть, если первый бит хеша сообщения равен нулю, Боб выбирает первое число из первой пары в открытом ключе. И так далее.

Затем Боб хеширует каждое из 256 чисел из подписи Алисы и получает 256 хешей. Если эти 256 хешей в точности соответствуют 256 хешам, которые он только что получил из открытого ключа Алисы, Боб считает подпись подлинной. Если не соответствуют — то фальшивой.

Стоит обратить внимание, что до того, как Алиса опубликует подпись к сообщению, никто не знает 2×256 случайных чисел в секретном ключе. Таким образом, никто не может создать правильный набор из 256 чисел для подписи. После того, как Алиса опубликует подпись, никто всё ещё не знает остальные 256 чисел, и, таким, образом, не может создать подпись для сообщений, имеющих иной хеш.

Пример

Пусть Алиса передаёт сообщение M = «Lamport» Бобу, подписывая его подписью Лэмпорта и используя при этом 8-битную хеш-функцию. То есть, изначальное сообщение будет преобразовано в 8-битный хеш.

Генерация ключей

Используя генератор случайных чисел, Алиса получает восемь пар случайных чисел. Эти 16 чисел являются закрытым ключом Алисы.

Закрытый ключ: $(13,$ $134)$ $(128,$ $67)$ $(25,$ $90)(78,$ $156)$ $(89,$ $37)$ $(234,$ $29)$ $(199,$ $74)$ $(12,$ $3)$

Чтобы получить открытый ключ, Алиса вычисляет хеш-значение для каждого числа из закрытого ключа.

Открытый ключ:

$(00101010,$ $10010101)$

$(01100111,$ $11010101)$

$(00101110,$ $11110111)$

$(00100101,$ $11011101)$

$(11100001,$ $00011000)$

$(11000110,$ $11001110)$

$(11001101,$ $11001001)$

$(11100011,$ $11111101)$

Получившийся открытый ключ Алиса публикует в общий доступ.

Подпись сообщения

Алиса хочет подписать сообщение M = «Lamport». Для этого она вычисляет значение хеш-функции от этого сообщения $H(M)=01011010$ и ставит в соответствие каждому биту хеша одно из значений в парах закрытого ключа, тем самым формируя подпись.

Подпись сообщения «Lamport»: $(13,$ $67,$ $25,$ $156,$ $37,$ $234,$ $74,$ $12)$

Проверка подписи

Боб получает подписанное сообщение «Lamport» и хочет проверить, действительно ли его послала Алиса. Для этого он использует открытый ключ, который опубликовала Алиса. Он преобразует полученное сообщение в хеш и каждому биту в получившемся хеше ставит в соответствие число из пары в открытом ключе. Затем он хеширует подпись сообщения и сравнивает два получившихся набора чисел. Если они равны, то подпись настоящая, и сообщения действительно посылала Алиса.

Набор чисел, полученный из открытого ключа:

$00101010,$

$11010101,$

$00101110,$

$11011101,$

$00011000,$

$11000110,$

$11001001,$

$11100011$

Хеш подписи:

$00101010,$

$11010101,$

$00101110,$

$11011101,$

$00011000,$

$11000110,$

$11001001,$

$11100011$

Так как данные наборы равны — подпись настоящая.

Математическое описание

Ключи

Пусть $k$ — положительное число, пусть $P=\{0,1\}^{k}$ — набор сообщений и пусть $f:\,Y\rightarrow Z$ — односторонняя функция.

Для каждого $1\leq i\leq k$ и $j\in \{0,1\}$, сторона, подписывающая сообщение, случайно выбирает $y_{i,j}\in Y$ и вычисляет $z_{i,j}=f(y_{i,j})$.

Секретный ключ $K$ состоит из $2k$ значений $y_{i,j}$. Открытый ключ состоит из $2k$ значений $z_{i,j}$.

Подпись сообщения

Пусть $m=m_{1}\ldots m_{k}\in \{0,1\}^{k}$ — сообщение.

Подпись сообщения — это $sign(m_{1}\ldots m_{k})=(y_{1,m_{1}},\ldots ,y_{k,m_{k}})=(s_{1},\ldots ,s_{k})$.

Проверка подписи

Сторона, валидирующая подпись, проверяет $f(s_{i})=z_{i,m_{i}}$ для всех $1\leq i\leq k$.

Чтобы подделать подпись сообщения криптоаналитику придется инвертировать одностороннюю функцию $f$, а это предполагается вычислительно невозможным.

Криптостойкость

Криптостойкость подписей Лэмпорта основана на криптостойкости хеш-функции.

Для каждой хеш-функции, которая генерирует n-битный дайджест, идеальная стойкость к восстановлению прообраза и к восстановлению второго прообраза подразумевает для каждого выполнения хеш-функции 2ⁿ операций и 2ⁿ бит памяти в классической вычислительной модели. Используя алгоритм Гровера, восстановление прообраза значения идеальной хеш-функции ограничено сверху O(2^n/2) операциями в квантовой вычислительной модели.

Подпись нескольких сообщений

Одним секретным ключом Лэмпорта может быть подписано только одно единственное сообщение. Это значит, что если подписано какое-то количество сообщений, должно быть опубликовано такое же количество открытых ключей. Но, если использовать дерево Меркла, составленное из открытых ключей, то вместо публикации всех открытых ключей, можно публиковать только вершину дерева. Это увеличивает размер подписи, так как часть хеш-дерева приходится включать в подпись, но это даёт возможность использовать один единственный хеш для проверки множества подписей. По такой схеме можно подписать $N=2^{n}$ сообщений, где $n$ — глубина дерева Меркла. То есть теоретически мы можем использовать один открытый ключ для любого количества сообщений.

Генерация ключей

Дерево Меркла с восемью листовыми элементами

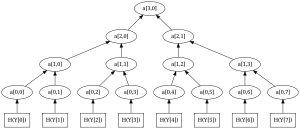
Для начала необходимо сгенерировать $2^{n}$ закрытых одноразовых ключей Лэмпорта $X_{i}$ и открытых одноразовых ключей Лэмпорта $Y_{i}$. Далее для каждого открытого ключа $Y_{i}$, где $1\leq i\leq 2^{n}$, вычисляется его хеш $h_{i}=H(Y_{i})$. И на основе этих значений $h_{i}$ строится дерево Меркла.

Пронумеруем узлы дерева $a_{i,j}$ таким образом, что индекс $i$ обозначает расстояние от этого узла до листового элемента, а индекс $j$ обозначает порядковый номер узла слева направо на одном уровне $i$.

В нашем дереве хеш значения $h_{i}$ являются листовыми элементами, то есть $h_{i}=a_{0,i}$. Каждый нелистовой узел дерева представляет из себя хеш-значение от соединения вместе двух детей, то есть $a_{1,0}=H(a_{0,0}||a_{0,1})$, $a_{2,0}=H(a_{1,0}||a_{1,1})$ и так далее.

Таким образом, мы имеем дерево, корневой элемент которого и является нашим открытым ключом $pub$.

Подпись сообщения и его проверка

Вычисление пути до вершины в дереве Меркла

Чтобы подписать сообщение по нашей схеме, сначала нужно подписать его одноразовой подписью Лэмпорта $sig'$. Это делается, используя одну из пар открытых/закрытых ключей $(X_{i},Y_{i},)$.

$a_{0,i}=H(X_{i})$ — соответствующий открытому ключу $X_{i}$ листовой элемент дерева. Путь от листового элемента $a_{0,i}$ дерева к его вершине состоит из элементов $A_{0},...A_{n}$, где $A_{0}=a_{0,i}$ — листовой элемент, а $A_{n}=a_{n,0}=pub$ — вершина дерева. Чтобы вычислить этот путь, нам необходимы все дети узлов $A_{1},...,A_{n}$. Мы знаем, что узел $A_{i}$ — дочерний элемент узла $A_{i+1}$. Чтобы вычислить следующий узел на пути к вершине нам нужны оба дочерних элемента узла $A_{i+1}$. Поэтому нам нужно знать «брата» узла $A_{i}$. Назовём его $auth_{i}$. Итак, $A_{i+1}=H(A_{i}||auth_{i})$. Следовательно, нам нужны $n$ узлов $auth_{0},...,auth_{n-1}$, чтобы вычислить вершину дерева. Мы вычисляем их и сохраняем.

Эти узлы в совокупности с одноразовой подписью $sig'$ сообщения $M$ составляют итоговую подпись $sig=(sig'||X_{i}||auth_{0}||auth_{1}||...||auth_{n-1})$.

Получатель сообщения имеет в распоряжении открытый ключ $pub$, сообщение $M$ и подпись $sig=(sig'||X_{i}||auth_{0}||auth_{1}||...||auth_{n-1})$. Сначала он проверяет одноразовую подпись $sig'$ сообщения $M$. Если она подлинна, получатель вычисляет $A_{0}=H(X_{i})$. И далее для $j=1,..,n-1$ вычисляет $A_{j}=H(A_{j-1}||auth_{j-1})$. Если $A_{n}$ оказывается равна $pub$, то подпись считается подлинной.

Различные оптимизации и реализации

Короткий секретный ключ

Вместо создания и хранения всех случайных чисел секретного ключа, можно хранить одно единственно число соответствующего размера. Обычно размер выбирается таким же, как и размер одного случайного числа в закрытом ключе. Этот ключ можно использовать как зерно для генератора случайных чисел (CSPRNG), чтобы можно было воссоздать всю последовательность случайных чисел секретного ключа, когда это понадобиться.

Тем же способом ключ может быть использован вместе с CSPRNG, чтобы создать множество ключей Лэмпорта. Предпочтительны CSPRNG, имеющие высокую криптостойкость, такие как BBS.

Короткий открытый ключ

Подпись Лэмпорта может быть использована вместе со списком хешей, что делает возможным включать в открытый ключ только один хеш. То есть, вместо $2k$ значений — $z_{ij}$. Чтобы иметь возможность сравнивать случайные числа в подписи с хешем в открытом ключе, все неиспользуемые в открытом ключе хеши, то есть, значения $(z_{ij})$ для любого $j\neq m_{i}$, должны быть включены в подпись. В результате открытый ключ становится существенно короче, а размер подписи увеличивается примерно в два раза.

Хеширование сообщения

Схема цифровой подписи Лэмпорта не требует, чтобы сообщение m было захешировано перед тем, как оно будет подписано. Хеширование может быть использовано, например, для подписания длинных сообщений, где подписываться будет хеш сообщения, а не оно само.

Сравнение с другими криптосистемами

Основные преимущества схемы одноразовой подписи Лэмпорта заключаются в том, что она может быть построена на любой односторонней функции, и в том, что её алгоритм подписи и проверки сообщения существенно быстрее алгоритмов систем многоразовой подписи. В то же время схема имеет ряд недостатков. Во-первых, недостатком является одноразовость ключей. То есть, при подписи каждого нового сообщения приходиться генерировать новую пару, что приводит к усложнению системы. Во-вторых, схема имеет недостаток в виде большого размера подписи и пары из открытого и закрытого ключей.

Данная система имеет потенциал в свете того, что потенциальная разработка квантового компьютера угрожает криптостойкости многих широко используемых алгоритмов, таких как RSA, в то время, как подпись Лэмпорта останется криптостойкой и в этом случае. В совокупности с деревьями Меркла, криптосистема Лэмпорта может быть использована для проверки подлинности множества сообщений, выступая как довольно эффективная схема цифровой подписи.

Литература

• Lamport L. Constructing digital signatures from a one-way function. — SRI International Computer Science Laboratory, 1979.
• Peikert K. Theoretical Foundations of Cryptography. — Georgia Tech, 2010. Архивная копия от 19 декабря 2013 на Wayback Machine
• Katz J. Introduction to Cryptography. — University of Maryland.
• Zaverucha G. Stinson R. Cheriton R. Short One-Time Signatures. — University of Waterloo, 2010.
• Garcia L. On security and efficiency of the Merkle signature scheme. — Darmstadt.