Накрывающий граф (UgtjdfgZpnw ijgs)

Граф C является накрывающим графом другого графа G, если имеется накрывающее отображение из множества вершин C в множество вершин G. Накрывающее отображение f является сюръекцией и локальным изоморфизмом — окрестность вершины v в C отображается биективно в окрестность f(v) в G.

Часто используется термин поднятие в качестве синонима для накрытия графа связанного графа.

В теории графов накрывающий граф может также относиться к подграфу, который содержит либо все рёбра (рёберное покрытие), либо все вершины (вершинное покрытие).

Комбинаторная формулировка накрывающих графов немедленно обобщается на случай мультиграфов. Если мы отождествим мультиграф с 1-мерным клеточным комплексом, накрывающий граф не что иное как специальный пример накрытий топологических пространств, так что допустима терминология теории накрытий, а именно, группа преобразования накрытия, универсальное накрытие, абелево накрытие и максимальное абелево накрытие^[1].

Определение

Пусть $G=(V_{1},E_{1})$ и $C=(V_{2},E_{2})$ будут два графа и пусть функция $f\colon V_{2}\to V_{1}$ сюръективна. Тогда f является накрывающим отображением из C в G, если для каждого $v\in V_{2}$ сужение f на окрестность вершины v является биекцией в окрестность вершины f(v) в G. Иначе говоря, f отображает рёбра, инцидентные v один-в-один в рёбра в инцидентные f(v).

Если существует накрывающее отображение из C в G, то C является накрывающим графом или подъёмом графа G, а G — факторграфом C. h-Подъём — это подъём, такой, что накрывающее отображение f имеет свойство, что для любой вершины v графа G, его расслоение $f^{-1}(v)$ имеет ровно h элементов.

Примеры

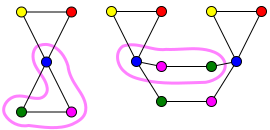
На следующем рисунке граф C является накрывающим графом графа H.

Накрывающее отображение f из C в H отражено цветами. Например, обе синие вершины C отображаются в синие вершины графа H. Отображение f сюръективно — каждая вершина графа H имеет прообраз в C. Более того, f отображает биективно каждого соседа вершины v из графа C в соседа вершины вершины f(v) из графа H.

Например, пусть v будет одной из пурпурных вершин из C. Она имеет два соседа в C, зелёную вершину u и голубую вершину t. Аналогично, пусть v′ будет пурпурной вершиной из H. Она имеет два соседа в H, зелёную вершину u′ и синюю вершину t′. Отображение f, суженное на {t, u, v}, является биекцией в {t′, u′, v′}. Это иллюстрирует следующий рисунок:

Аналогично, мы можем проверить, что окрестность синей вершины в C отображается один-в-один в окрестность синей вершины в H:

Двойное покрытие

В примере выше каждая вершина графа H имеет ровно 2 прообраза в C. Здесь H является 2-кратным накрытием или двойным накрытием графа C.

Для любого графа G можно построить двойное покрытие двудольным графом графа G, которое является и двудольным графом и двойным накрытием графа G одновременно. Двойное покрытие двудольным графом графа G является тензорным произведением $G\times K_{2}$ :

Если граф G уже двудолен, его двойное покрытие двудольным графом состоит из двух непересекающихся копий графа G. Граф может иметь много различных двойных покрытий, отличных от двойного покрытия двудольным графом.

Универсальное накрытие

Для любого связного графа G можно построить его граф универсального накрытия^[2]. Это частный случай более общей концепции универсального накрытия из топологии. Топологическое требование, чтобы универсальное накрытие было односвязным, преобразуется в терминах теории графов в требовании, чтобы граф был связен и не имел циклов, то есть был деревом. Граф универсального накрытия единственен (с точностью до изоморфизма). Если граф G является деревом, то G сам по себе является графом универсального накрытия графа G. Для любого другого конечного связного графа G граф универсального накрытия графа G является счётно бесконечным (но локально конечным) деревом.

Граф универсального накрытия T связного графа G можно построить следующим образом. Выбираем произвольную вершину r графа G в качестве начальной точки. Каждая вершина накрытия T является проходом без возврата, который начинается в r, то есть последовательность $w=(r,v_{1},v_{2},\dots ,v_{n})$ вершин графа G, такая, что

v_i и v_i+1 смежны в G для всех i, то есть w является проходом
$v_{i-1}\neq v_{i+1}$ для всех i, то есть без возврата.

Тогда две вершины T смежны, если одна является простым расширением другой — вершина $(r,v_{1},v_{2},\dots ,v_{n})$ смежна вершине $(r,v_{1},v_{2},\dots ,v_{n-1})$ . С точностью до изоморфизма то же самое дерево T получается независимо от выбора начальной точки r.

Накрывающее отображение f отображает вершину (r) из T в вершину r в G, а вершину $(r,v_{1},v_{2},\dots ,v_{n})$ из T в вершину v_n в G.

Примеры универсальных накрытий

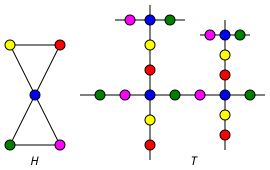
Следующий рисунок иллюстрирует граф универсального накрытия T графа H. Цвета показывают накрывающее отображение.

Для любого k все k-регулярные графы имеют одно и то же универсальное накрытие — бесконечное k-регулярное дерево.

Топологический кристалл

Бесконечнократный абелев накрывающий граф конечного (мульти)графа называется топологическим кристаллом, абстракцией кристаллической структуры, и является периодическим графом^[англ.]. Например, кристалл алмаза как граф представляет собой максимальный абелев накрывающий граф диполя^[англ.] с четырьмя рёбрами. Эта точка зрения, комбинированная с идеей «стандартных реализаций», оказывается полезной в систематическом построении (гипотетических) кристаллов^[1].

Планарное накрытие

Планарное накрытие графа — это конечное накрытие графа планарным графом. Свойство иметь планарное накрытие может быть описано запрещёнными минорами, однако точное описание такого вида остаётся неизвестным. Любой граф с вложением в проективную плоскость имеет планарное накрытие, получаемое из ориентируемого двойного накрытия^[англ.] проективной плоскости. В 1988 году Сэйю Нагами высказал предположение, что только эти графы и имеют планарные накрытия, но гипотеза остаётся недоказанной^[3].

Графы напряжений

Общий способ получения накрывающих графов использует графы напряжений^[англ.], в которых «дротики» данного графа G (то есть пары ориентированных рёбер, соответствующих неориентированным рёбрам G) помечены парами противоположных элементов (то есть элементом и ему обратного) из некоторой группы. Полученный из графа напряжений граф (производный граф) имеет в качестве вершин пары (v,x), где v — вершина графа G, а x является элементом группы. Дротик из v в w помечается элементом группы y из G соответствует ребру из (v,x) в (w,xy) в производном графе.

Универсальное накрытие можно рассматривать при таком подходе как производный граф графа напряжений, в котором рёбра остовного дерева графа помечены единичным элементом группы, а каждая оставшаяся пара дротиков помечена различными элементами свободной группы. Двудольное двойное накрытие можно рассматривать тогда как производный граф графа напряжений, в котором каждый дротик помечен ненулевым элементом группы порядка два.

Примечания

↑ ¹ ² Sunada, 2012.
↑ Angluin, 1980, с. 82–93.
↑ Hliněný, 2010, с. 525–536.

Литература

Toshikazu Sunada. Topological Crystallography -With a View Towards Discrete Geometric Analysis-. — Springer, 2012.
Petr Hliněný. 20 years of Negami's planar cover conjecture // Graphs and Combinatorics. — 2010. — Т. 26, вып. 4. — С. 525–536. — doi:10.1007/s00373-010-0934-9.
Chris Godsil, Gordon Royle. Sect. 6.8 // Algebraic Graph Theory. — Springer, 2004.
Amit Alon, Nathan Linial, Jiří Matoušek, Eyal Rozenman. Random lifts of graphs // Proceedings of the Twelfth Annual Symposium on Discrete Algorithms, January 7-9 (SODA 2001). — 2001. — С. 883–894. — ISBN 0-89871-490-7.
Dana Angluin. Local and global properties in networks of processors // Proceedings of the twelfth annual ACM symposium on Theory of computing (STOC 1980). — 1980. — ISBN 0-89791-017-6.

[_89ca38018a247f6c-1] ¹ ² Sunada, 2012.

[_05896f74f2983fac-2] Angluin, 1980, с. 82–93.

[_0794ccabcd98c66d-3] Hliněný, 2010, с. 525–536.

[1]

[2]

[3]