Надбарьерное отражение (Ug;Qgj,yjuky kmjg'yuny)

Надбарье́рное отраже́ние — термин, употребляемый в квантовой механике для описания невозможного в классической физике явления отражения движущейся частицы от потенциального барьера, максимальная высота которого $U_{max}$ меньше полной энергии частицы $E$. Коэффициент отражения определяется формой барьера (в одномерном случае $U(x)$), а также энергией и массой частицы. При этом коэффициент прохождения оказывается меньше единицы. Аналогичный эффект имеет место при прохождении частицы над потенциальной ступенькой или квантовой ямой.

Подход к рассмотрению

Независимо от профиля потенциала $U(x)$ движение частицы рассматривается с использованием стационарного уравнения Шрёдингера. Принимается, что частица движется слева направо (вдоль оси $x$), потенциал на большом расстоянии слева от барьера равен нулю, а справа $V_{0}$ (возможно, $V_{0}$ тоже равно нулю). В таком случае волновые функции слева и справа от барьера представляют собой плоские волны вида:

$\psi _{1}(x)=e^{ik_{1}x}+re^{-ik_{1}x}\,\,$ (далеко слева),

$\psi _{2}(x)=te^{ik_{2}x}\,\,$ (далеко справа).

$k_{1}={\sqrt {\frac {2m_{1}E}{\hbar ^{2}}}}$ и $k_{2}={\sqrt {\frac {2m_{2}(E-V_{0})}{\hbar ^{2}}}}$ — модули волновых векторов.

Масса $m$, вообще говоря, может различаться по областям, почему её символ и снабжён дополнительным индексом; $\hbar$ — постоянная Планка.

Если профиль $U(x)$ содержит резкие скачки, то на всех границах должно выполняться условие «сшивки» волновой функции $\psi$ и токов вероятности; последнее требует обеспечения непрерывности величины $\psi ^{'}/m$.

В процессе решения уравнения Шрёдингера определяются неизвестные константы $r$ и $t$, с использованием которых далее находятся коэффициенты отражения и прохождения:

$R=|r|^{2},\qquad T={\frac {k_{2}m_{1}}{m_{2}k_{1}}}|t|^{2}$.

Ниже представлены результаты такого рассмотрения для нескольких систем.

Примеры

Скачок потенциальной энергии

Основная статья: Потенциальная ступенька

Потенциальная энергия как функция координаты

Задача о переходе частицы, без изменения её массы, в область с другой потенциальной энергией $V_{0}=V$, имеет следующее решение:

$r={\frac {k_{1}-k_{2}}{k_{1}+k_{2}}},\qquad t={\frac {2k_{1}}{k_{1}+k_{2}}}$.

Коэффициенты отражения и прохождения составляют

$R=\left({\frac {1-{\sqrt {1-V/E}}}{1+{\sqrt {1-V/E}}}}\right)^{2},\quad T={\frac {4{\sqrt {1-V/E}}}{\left(1+{\sqrt {1-V/E}}\right)^{2}}}$.

Коэффициент отражения имеет конечное значение, но при стремлении $E$ к бесконечности он стремится к нулю.

Прямоугольный потенциальный барьер

Основная статья: Туннелирование через прямоугольный барьер

Потенциальная энергия как функция координаты

В случае прямоугольного барьера потенциал по обе его стороны нулевой (и $V_{0}=0$). Условия сшивки действуют на двух границах: при $x=0$ и $x=a$. Волновые векторы слева-справа и в барьере составляют

$k_{1}=k_{2}={\sqrt {\frac {2mE}{\hbar ^{2}}}},\qquad k_{b}={\sqrt {\frac {2m(E-V)}{\hbar ^{2}}}}$.

Результат для коэффициентов отражения и прохождения:

$R=1-T,\qquad T={\frac {1}{1+{\frac {(k_{1}^{2}-k_{b}^{2})^{2}}{4k_{1}^{2}k_{b}^{2}}}\sin ^{2}{k_{b}a}}}$.

При $E>V$ коэффициент отражения в общем случае отличен от нуля. Но при определённых энергиях $E$ становится $R=0$ из-за обнуления синуса.

Изменение эффективной массы

Потенциальная энергия, как функция координаты неизменна, но масса для частицы слева и справа от нуля различна

В данном случае коэффициенты $r$ и $t$ рассчитываются по формулам:

$r={\frac {{\sqrt {m_{1}}}-{\sqrt {m_{2}}}}{{\sqrt {m_{1}}}+{\sqrt {m_{2}}}}},\qquad t={\frac {2{\sqrt {m_{1}}}}{{\sqrt {m_{1}}}+{\sqrt {m_{2}}}}}$.

Соответственно, коэффициенты отражения и прохождения составят

$R=\left({\frac {{\sqrt {m_{1}}}-{\sqrt {m_{2}}}}{{\sqrt {m_{1}}}+{\sqrt {m_{2}}}}}\right)^{2},\qquad T={\frac {4{\sqrt {m_{1}m_{2}}}}{\left({\sqrt {m_{1}}}+{\sqrt {m_{2}}}\right)^{2}}}$.

При равенстве эффективных масс нет никакого отражения.

Бесконечная квантовая яма

Основная статья: Дельтообразный потенциал в квантовой механике

Прохождение частицы над ямой в виде дельта-функции

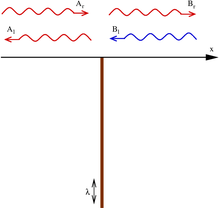
Дельтообразная квантовая яма — это потенциал вида $U(x)=\lambda /m\cdot \delta (x)$, где $\lambda ={\mbox{const}}<0$.

Примечание: при наличии $\delta$-функциональных особенностей потенциала несколько изменяются условия сшивки производных, вытекающие из требования непрерывности тока, см. конкретнее.

Коэффициенты отражения и прохождения для такой ямы составляют

$R=|r|^{2}={\frac {1}{1+{\frac {2m\hbar ^{2}E}{\lambda ^{2}}}}},\qquad T=|t|^{2}={\frac {1}{1+{\frac {\lambda ^{2}}{2m\hbar ^{2}E}}}}$.

Получается, что отражение частицы возможно при её надъямном движении с любой энергией $E$, хотя при повышении энергии вероятность отражения снижается.

Практическая релевантность

Все типы структур, представленные выше, встречаются или могут быть созданы на практике. В технологии полупроводниковых гетероструктур есть возможность получения многослойных систем с различными материалами. Поскольку возможности варьирования комбинаций материалов достаточно широки, вполне реально получение желаемых высот барьеров (от долей эВ до нескольких эВ) и величин эффективной массы. Соответственно, роль профиля потенциала $U(x)$ будет играть профиль зоны проводимости $E_{c}(x)$.

Литература

• Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5.
• Флюгге З. Задачи по квантовой механике. — Издательство ЛКИ, 2008. — Т. 1.