Механическая работа (By]guncyvtgx jgQkmg)

Работа
$A,W$
Размерность	L2MT−2
Единицы измерения
СИ	Дж
СГС	эрг
Примечания
скалярная величина

Механи́ческая рабо́та — физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел).

При постоянной силе и прямолинейном движении материальной точки, работа рассчитывается как произведение величины силы на перемещение и на косинус угла между векторами перемещения и силы: $A=Fs\cos(F,s)$. В более сложных случаях (непостоянная сила, криволинейное движение) это соотношение применимо к малому промежутку времени, а для вычисления полной работы необходимо суммирование по всем таким промежуткам.

В механике совершение работы над телом является единственной причиной изменения его энергии; в других областях физики энергия изменяется и за счёт иных факторов (например, в термодинамике — теплообмена).

Определение работы

По определению, «элементарная» (совершаемая за бесконечно малое время) работа — скалярное произведение действующей на материальную точку силы ${\vec {F}}$ на перемещение $d{\vec {s}}$, то есть

$\delta A={\vec {F}}\cdot d{\vec {s}}$.

Использование символа δ (а не $d$) обусловлено тем, что дифференциал работы не обязательно полный. Работа за конечный промежуток времени — интеграл элементарной работы:

$A=\int \delta A$.

Если имеется система материальных точек, выполняется суммирование по всем точкам. При наличии нескольких сил их работа определяется как работа равнодействующей (векторной суммы) этих сил.

Обозначения, размерность

Работа обычно обозначается заглавной буквой $A$ (от нем. Arbeit — работа, труд) или заглавной буквой $W$ (от англ. work — работа, труд).

Единицей измерения (размерностью) работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг. При этом

1 Дж = 1 кг·м²/с² = 1 Н·м;

1 эрг = 1 г·см²/с² = 1 дин·см;

1 эрг = 10⁻⁷ Дж.

Вычисление работы

Случай одной материальной точки

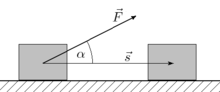
При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершённого точкой:

$A=F_{s}s=Fs\ \mathrm {cos} (F,s)={\vec {F}}\cdot {\vec {s}}$

Здесь «$\,\cdot \,$» обозначает скалярное произведение, ${\vec {s}}$ — вектор перемещения.

Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа этой силы равна нулю.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки:

$A=\int {\vec {F}}\cdot d{\vec {s}}$

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из перемещений $d{\vec {s}}$, если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат, интеграл определяется следующим образом:

$A=\int \limits _{{\vec {r}}_{0}}^{{\vec {r}}_{1}}{\vec {F}}\left({\vec {r}}\right)\cdot d{\vec {r}}$,

где ${\vec {r}}_{0}$ и ${\vec {r}}_{1}$ — радиус-векторы начального и конечного положения тела. Например, если движение происходит в плоскости $xy$, а ${\vec {F}}=F_{x}{\vec {e}}_{x}+F_{y}{\vec {e}}_{y}$ и $d{\vec {r}}=dx{\vec {e}}_{x}+dy{\vec {e}}_{y}$ (${\vec {e}}_{x}$, ${\vec {e}}_{y}$ — орты), то последний интеграл обретёт вид $A=\int (F_{x}+F_{y}|dy/dx|)dx$, где производная $dy/dx$ берётся для кривой $y(x)$, по которой движется точка.

Если сила ${\vec {F}}$ является консервативной (потенциальной), результат вычисления работы будет зависеть только от начального и финального положения точки, но не от траектории, по которой она перемещалась.

Случай системы точек или тела

Работа сил по перемещению системы из $N$ материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершённые над каждой точкой системы, суммируются в работу этих сил над системой):

$A=\sum A_{n},\quad n=1,2,..,N$.

Если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл:

$A=\int \delta A({\vec {r}}')=\iint {\frac {d{\vec {F}}({\vec {r}}')}{dV'}}\cdot d{\vec {r}}({\vec {r}}')dV'$,

где $dA({\vec {r}}')$ — работа по перемещению бесконечно малого фрагмента объёма тела $dV'$, локализованного около координаты ${\vec {r}}'$ (в системе отсчёта тела), от начального до финального положения, $d{\vec {F}}/dV'$ (Н/м³) — плотность действующей силы, а интегрирование проводится по всему объёму тела.

Эти формулы могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Работа и кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

С использованием второго закона Ньютона, позволяющего выразить силу через ускорение как ${\vec {F}}=m{\vec {a}}$ (где $m$ — масса материальной точки), а также соотношений $d{\vec {s}}=d{\vec {r}}={\vec {v}}dt$ и $d(v^{2})/dt=d({\vec {v}}\cdot {\vec {v}})/dt=2{\vec {a}}\cdot {\vec {v}}$, элементарная работа может быть переписана как

$\delta A=m{\vec {a}}\cdot {\vec {v}}dt={\frac {d}{dt}}\left({\frac {mv^{2}}{2}}\right)dt$.

При интегрировании от начального до финального момента получится

$A=\Delta \left({\frac {mv^{2}}{2}}\right)=\Delta E_{k}$,

где $E_{k}$ — кинетическая энергия. Для материальной точки она определяется как половина произведения массы этой точки на квадрат её скорости и выражается как $E_{k}=mv^{2}/2$. Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Работа и потенциальная энергия

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая $E_{p}$, такая, что

${\vec {F}}=-\nabla E_{p}$.

Здесь $\nabla$ — оператор набла. Если все силы, действующие на частицу, консервативны, и $E_{p}$ является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, то

${\vec {F}}\cdot d{\vec {s}}=-\nabla E_{p}\cdot d{\vec {s}}=-dE_{p}\Rightarrow -dE_{p}=dE_{k}\Rightarrow d(E_{k}+E_{p})=0$.

Данный результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия

$E=E_{k}+E_{p}$

в замкнутой системе, в которой действуют консервативные силы, является постоянной во времени. Этот закон широко используется при решении задач классической механики.

Работа силы в теоретической механике

Пусть материальная точка $M$ движется по непрерывно дифференцируемой кривой $G=\{r=r(s)\}$, где s — переменная длина дуги, $0\leq s\leq S$, и на неё действует сила $F(s)$, направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под $F(s)$ проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее).

Величина $F(\xi _{i})\triangle s_{i},\triangle s_{i}=s_{i}-s_{i-1},i=1,2,...,i_{\tau }$, называется элементарной работой силы $F$ на участке $G_{i}$ и принимается за приближённое значение работы, которую производит сила $F$, воздействующая на материальную точку, когда последняя проходит кривую $G_{i}$. Сумма всех элементарных работ $\sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}$ является интегральной суммой Римана функции $F(s)$.

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма $\sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}$ всех элементарных работ, когда мелкость $|\tau |$ разбиения $\tau$ стремится к нулю, называется работой силы $F$ вдоль кривой $G$.

Таким образом, если обозначить эту работу буквой $A$, то, в силу данного определения,

$A=\lim _{|\tau |\rightarrow 0}\sum _{i=1}^{i_{\tau }}F(\xi _{i})\triangle s_{i}=\int \limits _{0}^{s}F(s)ds$.

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра $t$ (например, времени) и если величина пройденного пути $s=s(t)$, $a\leq t\leq b$ является непрерывно дифференцируемой функцией, то из последней формулы получится

$A=\int \limits _{a}^{b}F[s(t)]s'(t)dt$.

Работа в термодинамике

Основная статья: Термодинамическая работа

В термодинамике работа, совершённая газом при расширении, рассчитывается как интеграл давления по объёму:

$A_{1\rightarrow 2}=\int \limits _{V_{1}}^{V_{2}}PdV$.

Работа, совершённая над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

• Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объёма, но и к любому процессу (изображаемому любой кривой в плоскости $PV$), в частности, к циклическим процессам.
• В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула непосредственно связана с механической работой, хотя, казалось бы, относится к другому разделу физики. Сила давления газа направлена ортогонально к каждой элементарной площадке и равна произведению давления $P$ на площадь $dS$ площадки. При расширении сосуда, работа, совершаемая газом для смещения $h$ одной такой элементарной площадки, составит

$dA=PdSh$.

Это и есть произведение давления на приращение объёма вблизи элементарной площадки. После суммирования по всем $dS$, получится результат, где будет уже полное приращение объёма, как и в главной формуле раздела.

См. также

• Закон сохранения энергии
• Теорема о кинетической энергии системы
• Механические приложения криволинейных интегралов

Литература

• История механики с древнейших времён до конца XVIII в. В 2 т. М.: Наука, 1972.
• Кирпичёв В. Л. Беседы о механике. М.-Л.: Гостехиздат, 1950.
• Льоцци М. История физики. М.: Мир, 1970.
• Мах Э. Принцип сохранения работы: История и корень его. СПб., 1909.
• Мах Э. Механика. Историко-критический очерк её развития. Ижевск: РХД, 2000.
• Тюлина И. А. История и методология механики. М.: Изд-во МГУ, 1979.