Корональная сейсмология (Tkjkugl,ugx vywvbklkinx)

Корональная сейсмология (англ. Coronal seismology) — метод исследования плазмы в солнечной короне с использованием данных о магнитогидродинамических волнах (МГД-волнах) и осцилляциях. Магнитная гидродинамика изучает динамику проводящих электричество жидкостей — в данном случае в роли жидкости выступает плазма короны. Наблюдаемые свойства волн (например, период колебаний, длина волны, амплитуда, временные и пространственные особенности (какова форма волнового возмущения?), характерные сценарии эволюции волн (ослабляется ли волна?) совместно с теоретическим моделированием волн (дисперсионные соотношения, уравнения эволюции волн, и т.д.) могут давать сведения о физических параметрах короны, которые невозможно измерить напрямую, такие как сила магнитного поля короны, альвеновская скорость, ^[1] коэффициенты диссипации в короне.^[2] Первоначально метод МГД-сейсмологии короны был предложен Й. Учидой (англ. Y. Uchida) в 1970 году^[3] для распространяющихся волн и Б. Робертсом (англ. B. Roberts) и др. в 1984 году^[4] для стоячих волн, но практическое применение метод получил только в конце 1990-х гг. из-за недостатка необходимого качества наблюдений. С философской точки зрения, сейсмология короны похожа на сейсмологию Земли, гелиосейсмологию и МГД-спектроскопию на лабораторных устройствах по изучению плазмы. Во всех этих областях науки для исследования среды используются волны разных типов.

Теоретической основой корональной сейсмологии является закон дисперсии для МГД-мод в цилиндре плазмы: области в плазме, не являющейся однородной в поперечном направлении и вытянутой вдоль магнитного поля. Такая модель хорошо работает при описании ряда структур в плазме, наблюдаемых в солнечной короне: корональных петель, волокон протуберанцев, струй и волокон. Подобные структуры являются волноводами для МГД-волн.^[5]

Типы магнитогидродинамических волн

Существует несколько видов МГД-мод, обладающих различными дисперсионными, поляризационными свойствами и параметрами распространения:

Изгибные (поперечные) моды (англ. kink, transverse modes), наклонные быстрые магнитоакустические волны, направляемые структурой плазмы; происходит смещение оси структуры плазмы. Такие моды слабо подвержены сжатию, могут наблюдаться в виде периодических стоячих или распространяющихся смещений структур короны, например, корональных петель. Частота поперечных мод определяется уравнением

\omega _{K}={\sqrt {\frac {2k_{z}B^{2}}{\mu (\rho _{i}+\rho _{e})}}}.

При поперечных модах азимутальное волновое число в цилиндрической модели петли $m$ равно 1, это означает, что цилиндр колеблется, но края при этом остаются неподвижными.

"Сосисочные" моды (англ. sausage modes), также наклонные быстрые магнитоакустические волны, направляемые структурой плазмы; при данной моде возникают расширения и сжатия структуры плазмы, но ось не перемещается. Такие моды подвержены сжатию и могут приводить к существенным изменениям абсолютной величины магнитного поля в колеблющейся структуре. Частота данных мод задаётся выражением

\omega _{S}={\sqrt {\frac {k_{z}^{2}B^{2}}{\mu \rho _{e}}}}.

Для "сосисочных" мод параметр $m$ равен 0; это означает, что структура "дышит", но краевые точки также остаются неподвижными.

Медленные, акустические (долготные) моды (англ. acoustic) являются медленными магнитоакустическими волнами, распространяющимися в основном вдоль линий магнитного поля по структуре плазмы; такие моды наиболее подвержены сжатию. Возмущение магнитного поля пренебрежимо мало. Частота медленных мод задаётся выражением

\omega _{L}={\sqrt {k_{z}^{2}\left({\frac {C_{s}^{2}C_{A}^{2}}{C_{s}^{2}+C_{A}^{2}}}\right)}}.

Здесь $C_{s}$ является скоростью звука, $C_{A}$ — альвеновская скорость.

Крутильные (альвеновские) моды (англ. torsional, twist mode) — это несжимаемые поперечные возмущения магнитного поля вдоль отдельных поверхностей. В противоположность поперечным модам торсионные моды нельзя пронаблюдать на инструментах, получающих изображение области, поскольку они не приводят к смещению оси структуры или ее границы. Частота задаётся выражением

\omega _{A}={\sqrt {\frac {k_{z}^{2}B^{2}}{\mu \rho _{i}}}}

Наблюдения

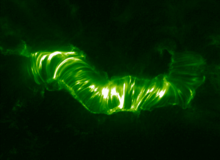
Волны и колебательные процессы наблюдаются в горячей плазме короны в основном в экстремальном ультрафиолетовом, оптическом и микроволновом диапазонах на целой серии космических и наземных инструментов, например, Solar and Heliospheric Observatory (SOHO), Transition Region and Coronal Explorer (TRACE), радиогелиографе Нобеяма (NoRH, см. Радиообсерватория Нобеяма). Исследователи различают сжимаемые волны в полярных факелах и у основания корональных петель, создаваемые вспышками поперечные колебания в петлях, акустические колебания в петлях, распространяющиеся поперечные колебания в петлях и структурах над арками (аркой называем набор близко расположенных петель, образующих цилиндрическую структуру, см. изображение справа), "сосисочные" колебания вспыхивающих петель, колебания в протуберанцах и волокнах; этот список периодически пополняется.

Корональная сейсмология является одной из целей изучения инструмента (AIA) миссии Solar Dynamics Observatory (SDO).

Предполагается, что Parker Solar Probe сможет провести измерения солнечного магнитного поля, солнечного ветра и параметров короны. Аппарат оснащён магнетометром и сенсором для определения волн плазмы, что позволит провести измерения с беспрецедентной точностью.

Выводы

Потенциал такого раздела астрономии, как корональная сейсмология, в области оценки параметров магнитного поля короны, вертикального масштаба плотности, "тонкой структуры" (под этим термином понимается вариация структуры неоднородных образований таких как неоднородные корональные петли) и нагрева был показан различными группами исследователей. Работы, относящиеся к корональному магнитному полю, упоминались выше.^[1] Было показано, что достаточно широкие медленные магнитоакустические волны, согласующиеся с наблюдениями в низкочастотной области спектра, могут создавать темп передачи тепла достаточный для нагрева корональной петли.^[6] Теоретически исследовались поперечные колебания корональных петель, обладающих переменными круговым поперечным сечением и плотностью плазмы в долготном направлении. Было выведено дифференциально уравнение второго порядка для описания смещения оси петли. Решение уравнения совместно с граничными условиями определяет собственные частоты и собственные моды. Шкалу высот плотности в короне можно оценить, используя наблюдаемое отношение фундаментальной частоты и первого обертона поперечных колебаний петли.^[7] О тонкой структуре короны известно немного. Проводится анализ данных о колебаниях доплеровского смещения в горячих активных областях, полученных на инструменте SUMER космической обсерватории SOHO. Спектры были сняты вдоль щели с угловым размером 300 секунд, расположенной в направлении короны над активными областями. Некоторые колебания характеризовались распространением фазы вдоль щели в одном или обоих направлениях при видимой скорости в интервале 8–102 км/с, также наблюдалась существенно различная интенсивность и ширина линий вдоль щели. Эти особенности можно объяснить возбуждением колебаний у основания неоднородной корональной петли, например, петли с тонкой структурой.^[8]

Примечания

↑ ¹ ² Nakariakov, V. M.; Ofman, L. Determination of the coronal magnetic field by coronal loop oscillations (англ.) // Astronomy and Astrophysics : journal. — 2001. — Vol. 372, no. 3. — P. L53—L56. — doi:10.1051/0004-6361:20010607. — Bibcode: 2001A&A...372L..53N. Архивировано 23 сентября 2017 года.
↑ Nakariakov, V. M.; Ofman, L.; Deluca, E. E.; Roberts, B.; Davila, J. M. TRACE observation of damped coronal loop oscillations: Implications for coronal heating (англ.) // Science : journal. — 1999. — Vol. 285, no. 5429. — P. 862—864. — doi:10.1126/science.285.5429.862. — Bibcode: 1999Sci...285..862N. — PMID 10436148.
↑ Uchida, Y. Diagnosis of coronal magnetic structure by flare-associated hydromagnetic disturbances (англ.) // Publications of the Astronomical Society of Japan^[англ.] : journal. — 1970. — Vol. 22. — P. 341—364. — Bibcode: 1970PASJ...22..341U.
↑ Roberts, B.; Edwin, P. M.; Benz, A. O. On coronal oscillations (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1984. — Vol. 279. — P. 857—865. — doi:10.1086/161956. — Bibcode: 1984ApJ...279..857R.
↑ Nakariakov, V. M.; Verwichte, E. Coronal Waves and Oscillations (англ.) // Solar Physics^[англ.] : journal. — 2005. — Vol. 2, no. 1. — P. 3. — doi:10.12942/lrsp-2005-3. — Bibcode: 2005LRSP....2....3N.
↑ Tsiklauri, D.; Nakariakov, V. M. Wide-spectrum slow magnetoacoustic waves in coronal loops (англ.) // Astronomy and Astrophysics : journal. — 2001. — Vol. 379, no. 3. — P. 1106—1112. — doi:10.1051/0004-6361:20011378. — Bibcode: 2001A&A...379.1106T. — arXiv:astro-ph/0107579.
↑ Ruderman, M. S.; Verth, G.; Erdelyi, R. Transverse Oscillations of Longitudinally Stratified Coronal Loops with Variable Cross Section (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2008. — Vol. 686, no. 1. — P. 694—700. — doi:10.1086/591444. — Bibcode: 2008ApJ...686..694R.
↑ Wang, T. J. et al. Hot coronal loop oscillations observed with SUMER: Examples and statistics (англ.) // Astronomy and Astrophysics : journal. — 2003. — Vol. 406, no. 3. — P. 1105—1121. — doi:10.1051/0004-6361:20030858. — Bibcode: 2003A&A...406.1105W.

Литература

Nakariakov, V. M.; Verwichte, E. Coronal Waves and Oscillations (англ.) // Solar Physics^[англ.] : journal. — 2005. — Vol. 2, no. 1. — P. 3. — doi:10.12942/lrsp-2005-3. — Bibcode: 2005LRSP....2....3N.
Roberts, B., Nakariakov, V.M., "Coronal seismology – a new science", Frontiers 15, 2003
Verwichte, E., Plasma diagnostics using MHD waves
Stepanov, A.V., Zaitsev, V.V. and Nakariakov, V.M., "Coronal Seismology" Wiley-VCH 2012 ISBN 978-3527409945

[Nakariakov2001-1] ¹ ² Nakariakov, V. M.; Ofman, L. Determination of the coronal magnetic field by coronal loop oscillations (англ.) // Astronomy and Astrophysics : journal. — 2001. — Vol. 372, no. 3. — P. L53—L56. — doi:10.1051/0004-6361:20010607. — Bibcode: 2001A&A...372L..53N. Архивировано 23 сентября 2017 года.

[2] Nakariakov, V. M.; Ofman, L.; Deluca, E. E.; Roberts, B.; Davila, J. M. TRACE observation of damped coronal loop oscillations: Implications for coronal heating (англ.) // Science : journal. — 1999. — Vol. 285, no. 5429. — P. 862—864. — doi:10.1126/science.285.5429.862. — Bibcode: 1999Sci...285..862N. — PMID 10436148.

[3] Uchida, Y. Diagnosis of coronal magnetic structure by flare-associated hydromagnetic disturbances (англ.) // Publications of the Astronomical Society of Japan^[англ.] : journal. — 1970. — Vol. 22. — P. 341—364. — Bibcode: 1970PASJ...22..341U.

[4] Roberts, B.; Edwin, P. M.; Benz, A. O. On coronal oscillations (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1984. — Vol. 279. — P. 857—865. — doi:10.1086/161956. — Bibcode: 1984ApJ...279..857R.

[5] Nakariakov, V. M.; Verwichte, E. Coronal Waves and Oscillations (англ.) // Solar Physics^[англ.] : journal. — 2005. — Vol. 2, no. 1. — P. 3. — doi:10.12942/lrsp-2005-3. — Bibcode: 2005LRSP....2....3N.

[6] Tsiklauri, D.; Nakariakov, V. M. Wide-spectrum slow magnetoacoustic waves in coronal loops (англ.) // Astronomy and Astrophysics : journal. — 2001. — Vol. 379, no. 3. — P. 1106—1112. — doi:10.1051/0004-6361:20011378. — Bibcode: 2001A&A...379.1106T. — arXiv:astro-ph/0107579.

[7] Ruderman, M. S.; Verth, G.; Erdelyi, R. Transverse Oscillations of Longitudinally Stratified Coronal Loops with Variable Cross Section (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2008. — Vol. 686, no. 1. — P. 694—700. — doi:10.1086/591444. — Bibcode: 2008ApJ...686..694R.

[8] Wang, T. J. et al. Hot coronal loop oscillations observed with SUMER: Examples and statistics (англ.) // Astronomy and Astrophysics : journal. — 2003. — Vol. 406, no. 3. — P. 1105—1121. — doi:10.1051/0004-6361:20030858. — Bibcode: 2003A&A...406.1105W.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]