Гелиосейсмология (Iylnkvywvbklkinx)

Перейти к навигации Перейти к поиску
Созданное на компьютере изображение показывает модель акустических колебаний p-моды на Солнце как внутри звезды, так и на поверхности (l=20, m=16, and n=14). Отметим, что увеличение скорости звука пр мере приближения волн к центру Солнца приводит к соответствующему увеличению длины волны.

Гелиосейсмология (англ. Helioseismology) — раздел астрономии, изучающий внутреннюю структуру и кинематику Солнца по распространению сейсмических волн, в частности акустических (p-волн) и поверхностных гравитационных волн (f-волны).[1][2] Данный раздел был разработан по аналогии с геосейсмологией (первоначально называвшейся сейсмологией), также появилась астросейсмология,[3] в которой исследовались сейсмические волны с целью получения информации о внутреннем строении других звёзд. Поскольку Солнце проявляет свойства жидкого тела, то в первом приближении в нём не могут существовать сдвиговые волны (s-волны), подобные сейсмическим волнам на Земле. Исключением являются магнито-акустические волны, по-видимому, проявляющиеся в основном в атмосфере.[4] Гелиосейсмические волны создаются турбулентностью в конвективной зоне непосредственно под поверхностью Солнца.[5] Определённые частоты усиливаются при интерференции, что приводит к резонансам. Резонансные волны отражаются вблизи фотосферы (видимой поверхности Солнца), где их можно наблюдать. Колебания заметны почти в любых рядах изображений Солнца, но наилучшим образом проявляются в виде доплеровского смещения линий поглощения в атмосфере. Детали распространения сейсмических волн в Солнце, полученные из резонансных частот, помогают выявить внутреннее строение Солнца, благодаря чему астрофизики могут разрабатывать очень подробные модели гидростатической стратификации[6] и внутренней угловой скорости.[7][8] Это позволило оценить квадрупольный момент,[7] , и моменты более высоких порядков [9] внешнего гравитационного потенциала Солнца. Подобная оценка является более точной и надёжной по сравнению с попыткой получения данных параметров из сплюснутости видимого диска.[10][11] Вместе с измерениями орбиты Меркурия и космических аппаратов полученные выше результаты согласуются с выводами общей теории относительности.[12]

Гелиосейсмология помогла исключить вероятность того, что проблема солнечных нейтрино являлась результатом некорректной статичной модели внутренней области Солнца.[13] [14] [15] Выявленные в рамках гелиосейсмологии особенности включают различие вращения внешней конвективной зоны и внутренней зоны лучистого переноса, что, как считается некоторыми учёными, создаёт магнитное поле по крайней мере во внешних слоях Солнца с помощью динамо-механизма.[16][17] Угловая скорость в конвективной зоне уменьшается от экватора к полюсам, слабо меняясь с глубиной. Зона лучистого переноса вращается почти равномерно. Две данные области разделены слоем (тахоклин),[18][19] слишком тонким для того, чтобы его можно было разрешить только при сейсмологическом анализе. В конвективной зоне существуют струйные течения плазмы в тысячах километрах под поверхностью.[20] Струйные течения образуют широкий фронт на экваторе, разбиваясь на меньшие вихри-циклоны на высоких широтах. Колебания являются изменениями дифференциального вращения во времени. Они представляют собой чередующиеся полосы быстрого и медленного вращения. Поскольку общепринятого теоретического обоснования данного явления нет, но оно тесно связано с циклом солнечной активности, поскольку имеет период 11 лет; в первый раз явление наблюдалось в 1980 году.[21]

Гелиосейсмологию можно использовать для получения сведений о дальней стороне Солнца от Земли,[22] включая солнечные пятна. Говоря простыми словами, солнечные пятна поглощают и отклоняют гелиосейсмические волны, что сказывается в момент входа в фотосферу.[23] Для прогнозирования космической погоды сейсмические изображения центральной части дальней стороны Солнца почти непрерывно получают с 2000 года при анализе данных обсерватории SOHO, а с 2001 по тем же данным получают полную картину дальней стороны Солнца.

Виды колебаний на Солнце

[править | править код]
Спектр колебаний Солнца низкого разрешения, полученный инструментом GOLF (англ. Global Oscillations at Low Frequencies) обсерватории SOHO в период с 19 февраля по 25 марта 1996 года. По горизонтальной оси отложена частота в миллигерцах, вертикальная ось представлена в логарифмическом масштабе. 5-минутные колебания представляют собой ряды линий p-волн справа между 2 мГц и 7 мГц.

Отдельные колебания на Солнце затухают; при отсутствии постоянного поддерживающего воздействия они исчезают за несколько дней. Резонансная интерференция между распространяющимися волнами создаёт глобальные стоячие волны, известные как нормальные моды колебаний. Анализ данных мод составляет предмет глобальной гелиосейсмологии.

Моды солнечных осцилляций делят на три основные категории в соответствии с их основной восстанавливающей силой: давление преобладает в p-модах, плавучесть — в гравитационных колебаниях, как внутренних (g-моды), так и поверхностных (f-моды):

  • динамика p-мод определяется изменением скорости звука внутри Солнца. Колебания с амплитудами, достаточно большими для обнаружения, обладают частотами от 1 до 5 мГц, причём особенно сильны колебания в интервале частот от 2 до 4 мГц, называемые "5-минутными колебаниями" (цикл в 5 минут соответствует 1/300 цикла в секунду, т.е. 3,33 мГц). На поверхности Солнца отдельные p-волны имеют амплитуды скорости около 10 см/с, что предполагает амплитуду смещения в несколько метров и флуктуации интенсивности несколько миллионных долей; такие волны можно обнаружить по анализу допплеровского смещения или при исследовании интенсивности спектральных линий. С помощью инструментов GONG и MDI (англ. Michelson Doppler Imager) на борту космического аппарата SOHO были обнаружены тысячи p-волн с высоким и средним значением l (см. ниже), причём волны со значением l меньше 200 чётко разделяются.[24] Моды с очень малыми степенями более успешно наблюдаются при суммировании излучения по всему изображению Солнца как с помощью назменых обсерваторий, таких как BiSON,[25] распределённых по поверхности Земли для постоянного получения изображений, так и с помощью космических обсерваторий (инструмент GOLF в космической обсерватории SOHO).[26]
  • g-моды представляют собой стоячие внутренние гравитационные волны, восстанавливающая сила которых основана на отрицательной плавучести смещённого по вертикали вещества. Имеют сравнительно малую частоту (0-0,4 мГц). Данные волны связаны или с внутренней областью Солнца под конвективной зоной (внутренние 70% радиуса), или с атмосферой. Поскольку подобные волны не могут распространяться через конвективно неустойчивые области (в которых градиент температуры превышает адиабатический градиент, плавучесть положительна и сила, действующая на смещённый элемент вещества, не является восстанавливающей), то на поверхности практически не наблюдаются. g-моды называют эванесцентными волнами в конвективной зоне; считается, что амплитуда остаточной скорости составляет всего несколько миллиметров в секунду в фотосфере.[27] С 1980-х годов было несколько заявлений об обнаружении g-волн; в 2007 году такое заявление было сделано по результатам анализа полученных с помощью инструмента GOLF данных.[28] На конференции GONG2008 / SOHO XXI коллектив учёных (англ. Phoebus group) объявила о том, что данные открытия подтвердить не удалось, был указан верхний предел для амплитуд g-волн на уровне 3 мм/с, что соответствует пределу обнаружения инструмента GOLF. Данный коллектив учёных недавно (2009 год) опубликовал обзор текущего объёма знаний о g-моде колебаний.[29]
  • f-моды представляют собой гравитационные волны; за исключением мод наименьшей степени l, связаны с близкими к поверхности слоями Солнца, проникают на глубину порядка R/l (R — радиус Солнца) под фотосферу. Частоты f-мод высокой степени определяются в основном только гравитацией на поверхности и горизонтальной длиной волны и очень слабо зависят от строения Солнца. На Земле аналогами таких волн являются волны Стокса, в предельном случае высоких значений l они удовлетворяют тому же дисперсионному соотношению. Отклонения от данного предельного соотношения дают информацию о распределении плотности в поверхностных слоях Солнца.[30] Допплеровские смещения, создаваемые адвекцией, измерялись на инструменте MDI, что позволило получить ограничения на горизонтальные течения под поверхностью Солнца.[31]

Анализ данных о колебаниях

[править | править код]
Спектр мощности солнечных колебаний (), построенный на основе анализа 144 дней данных инструмента MDI космической обсерватории SOHO.[32] Цветовая шкала является логарифмической. По мере увеличения абсциссы моды отдельных частот образуют хорошо различимые хребты, каждый соответствует последовательности мод низкого порядка.

Гелиосейсмические волны имеют очень малые амплитуды, их можно описать в виде суперпозиции решений линеаризованных волновых уравнений. Поскольку Солнце почти сферическое, то пространственную структуру данных волн можно представить в сферической системе координат в виде произведения ортонормированных поверхностных гармоник по координатам и и функции амплитуды, зависящей от . Обычно в качестве базисных функций для сферических гармоник рассматривают произведение exp(i ) и присоединённых функций Лежандра от cos степени и (aзимутального) порядка . В целом фоновая структура почти не меняется в течение одного периода колебаний, поэтому изменение во времени можно считать мультипликативной синусоидальной функцией от , частоты которой являются последовательностью собственных значений волновой функции и обозначаются порядковым числом . Степень является полным числом узловых окружностей на поверхности постоянной , азимутальный порядок является количеством полных узловых окружностей, пересекающих экватор; порядок для f-мод равен нулю, для p/g-мод он отсчитывается вверх/вниз в соответствии с количеством радиальных узлов собственной функции; частота является строго возрастающей функцией при постоянных и . Пример подобной моды приведён справа вверху данной статьи.

В получаемых из временных рядов спектров Солнца данных колебания накладываются друг на друга. Были обнаружены тысячи мод (а полное число оценивается в миллионы). Для получения информации об отдельных модах используются методы анализа Фурье. Основная идея состоит в том, что ограниченная функция в ограниченной области может быть представлена в виде взвешенной суммы ортогональных гармонических функций (базисные функции), которые в одном измерении являются периодическими функциями (синусами и косинусами различных частот). Для определения вклада (амплитуды) каждой базисной функции в применяется преобразование Фурье: по существу, определяется проекция (скалярное произведение функций) на базисные функции над заданной областью; на практике применяется более сложный и быстрый метод по сравнению с явным выражением проекций.

Если бы Солнце было сферически-симметричным, то собственные частоты были бы вырожденными относительно , поскольку все рассматриваемые системы сферических полярных координат были бы неразличимы. Вращение Солнца создаёт утолщение на экваторе, что наряду с другими несферическими возмущениями (например, солнечные пятна) нарушает симметрию. В общем частоты звёздных колебаний зависят от всех трёх квантовых чисел , и . Удобно разделять частоты в виде мультиплетных частот , взвешенных по , соответствующих сферически-симметричной структуре звезды, и рассматривать величины , определяемые несферичностью.

Анализ данных о колебаниях нацелен на разделение компонентов с разными частотами. В случае Солнца колебания можно наблюдать в виде функции от положения точки на диске и от времени. Проекция на собственные пространственные функции помогает отделить и , хотя результат содержит вклад многих других гармоник, поскольку на практике только треть полной поверхности Солнца можно эффективно измерить. Усреднение по поверхности звезды, происходящее при наблюдении осцилляций других звёзд, аналогично наблюдению полного диска Солнца инструментами BiSON и GOLF. После проецирования осуществляется преобразование Фурье по времени, после чего при адекватном разрешении можно определить частоты отдельных мод.

Заметим, что данные об осцилляциях представляют собой дискретные множества в пространстве и времени, причём они подвержены ошибкам наблюдений. При осуществлении преобразований применяется интерполяция, что также вносит дополнительные ошибки.

Данное обсуждение взято из записей лекций Йоргена Кристенсена-Дальсгаарда (англ. Jørgen Christensen-Dalsgaard) по звёздным колебаниям.[33]

Инверсия

[править | править код]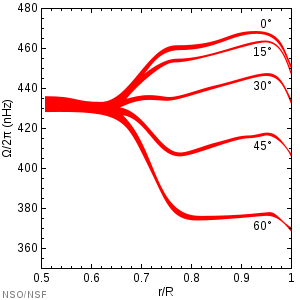
Внутреннее вращение в Солнце; во внешней части конвективной зоны вращение дифференциальное, в центральной части (зона лучистого переноса) вращение почти однородное. Область перехода между двумя зонами называется тахоклином.

Информацию о гелиосейсмических волнах, получаемую при преобразовании данных о колебаниях, можно использовать для получения сведений о таких параметрах, как скорость звука внутри Солнца, внутреннее дифференциальное вращение. Уравнения и аналитические соотношения выводятся таким образом, чтобы соотносить интересующие параметры с наблюдательными данными. Применяемые численные методы таковы, что позволяют получить максимум информации о внутренних особенностях Солнца с минимальной возможной ошибкой. Такой процесс называется гелиосейсмической инверсией.

Как пример, расщепление частот колебаний (англ. oscillation frequency splitting) можно связать с помощью интеграла с угловой скоростью внутри Солнца.[33]

Внутренняя структура

[править | править код]

Гелиосейсмические наблюдения выявляют внутреннюю равномерно вращающуюся область и дифференциально вращающуюся оболочку Солнца, примерно соответствующие зоне лучистого переноса и конвективной зоне.[16] См. диаграмму справа. Переходный слой называется тахоклином.

Гелиосейсмическая датировка

[править | править код]

Возраст Солнца можно оценить при исследовании гелиосейсмической активности,[34] [35] [36] [37] поскольку распространение акустических волн глубоко внутри Солнца зависит от состава Солнца, в частности от количества гелия и водорода в ядре. Поскольку Солнце превращает водород в гелий в течение своей жизни, то современное количество гелия в ядре можно использовать для определения возраста Солнца с помощью численных моделей звёздной эволюции в применении к Солнцу (стандартная солнечная модель). Данный метод подтверждает оценки возраста Солнечной системы, полученные при радиометрической датировке метеоритов.[38]

Локальная гелиосейсмология

[править | править код]

Целью локальной гелиосейсмологии[39] является интерпретация полного волнового поля, наблюдаемого на поверхности, а не только частот мод. Глобальная гелиосейсмология исследует стоячие волны во всём Солнце, а локальная гелиосейсмология исследует распространение волн в отдельных частях Солнца. Исследуется ряд различных явлений на Солнце, включая солнечные пятна, флоккулы, супергрануляцию, конвекцию в гигантских ячейках, эволюцию активных магнитных областей, меридиональную циркуляцию, вращение Солнца.[40] Локальная гелиосейсмология предоставляет трёхмерную картину внутренней области Солнца, что важно для понимания крупномасштабных течений, магнитных структур и их взаимодействий внутри Солнца.

Существует ряд методов, применяемых в данной области, включая следующие.

  • Спектральный метод Фурье–Ханкеля (впервые в данной области применили Браун и Дюваль[41] изначально применялся для определения поглощения волн солнечными пятнами.
  • Анализ круговых диаграмм, предложенный ф.Хиллом,[42]) используется для получения скорости и направления горизонтальных течений под поверхностью Солнца при наблюдении допплеровского смещения акустических волн в спектре мощности солнечных колебаний, вычисляемом в ряде участков солнечной поверхности (обычно 15° × 15°). Данный метод является обобщением глобальной гелиосейсмологии в применении к отдельным областям на Солнце. Например, можно сравнить скорость звука и показатель адиабаты в магнитно активных и неактивных областях.[43]
  • Пространственно-временная гелиосейсмология (предложили Дюваль и др.[44]) направлена на измерение и интерпретацию времени прохождения солнечных волн между двумя точками на поверхности Солнца. Аномалии во времени прохождения свидетельствуют о сейсмической природе неоднородностей вблизи луча, соединяющего данные точки.

Необходимо решить обратную задачу для определения локальной структуры и динамики внутренней области Солнца.[45]

  • Гелиосейсмическая голография, подробно рассмотренная Линдси и Брауном для целей получения изображений дальней стороны Солнца,[22] является особым вариантом чувствительной к фазе голографии. Идея состоит в том, чтобы использовать волновое поле видимого диска для исследования активных областей на противоположной стороне Солнца. Основная идея гелиосейсмической голографии: наблюдаемое волновое поле (например, допплеровское смещение, наблюдаемое на поверхности Солнца) можно использовать для оценки волнового поля в любом месте внутренней области Солнца в любой момент времени. В этом смысле голография похожа на метод сейсмической миграции, разработанный в геофизике. Метод голографии позволяет получить сейсмическое изображение солнечных вспышек.[46] Акустическая голография, применённая к данным MDI, помогает обнаружить источники и области исчезновения акустических волн на Солнце. Браун и Фань [47] обнаружили область с низким акустическим излучением в полосе частот 3 – 4 мГц, простирающейся далеко за пределы солнечных пятен в область спокойного Солнца. Браун и Линдси[48] обнаружили излучение высокой частоты (‘акустические сияния’), окружающие активные области.
  • Прямое моделирование.[49] Идея состоит в оценке течений под поверхностью исходя из инверсии корреляций частоты и волнового числа, наблюдаемых в волновом поле. Вудорд[49] приводит практическую демонстрацию возможности данного метода обнаруживать близкие к поверхности потоки по данным о f-волнах в спектре.

Данный раздел основан на материале книги Laurent Gizon и Aaron C. Birch, "Local Helioseismology", Living Rev. Solar Phys. 2, (2005), 6.

Примечания

[править | править код]
  1. ↑ Deubner, F.L.; Gough, D.O. Helioseismology: Oscillations as a Diagnostic of the Solar Interior (англ.) // Annual Reviews of Astronomy and Astrophysics[англ.] : journal. — 1984. — Vol. 22. — P. 593—619. — doi:10.1146/annurev.aa.22.090184.003113. — Bibcode: 1984ARA&A..22..593D.
  2. ↑ Алексей Понятов. Услышать звуки звёзд // Наука и жизнь. — 2018. — № 1. — С. 40—47. Архивировано 14 января 2018 года.
  3. ↑ Gough, D.O. Beginnings of asteroseismology (англ.) // Nature. — 1985. — Vol. 314. — P. 14—15. — doi:10.1038/314014a0. — Bibcode: 1985Natur.314...14G.
  4. ↑ Campbell, W.R.; Roberts, B. The influence of a chromospheric magnetic field on the solar p- and f-modes (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1989. — March (vol. 338). — P. 538—556. — doi:10.1086/167216. — Bibcode: 1989ApJ...338..538C.
  5. ↑ Goldreich, P.; Keeley, D.A. Solar seismology. II - The stochastic excitation of the solar p-modes by turbulent convection (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1977. — February (vol. 212). — P. 243—251. — doi:10.1086/155043. — Bibcode: 1977ApJ...212..243G.
  6. ↑ ChristensenDalsgaard, J.; Duvall Jr., T.L.; Gough, D.O.; Harvey, J.W.; Rhodes Jr, E.J. Speed of sound in the solar interior (англ.) // Nature. — 1985. — May (vol. 315). — P. 378—382. — doi:10.1038/315378a0. — Bibcode: 1985Natur.315..378C.
  7. ↑ 1 2 Duvall Jr., T.L.; Dziembowski, W.A.; Goode, P.R.; Gough, D.O.; Harvey, J.W.; Leibacher, J.W. Internal rotation of the sun (англ.) // Nature. — 1984. — July (vol. 310). — P. 22—25. — doi:10.1038/310022a0. — Bibcode: 1984Natur.310...22D.
  8. ↑ Schou, J.; Antia, H.M.; Basu, S.; Bogart, R.S.; Bush, R.I.; Chitre, S.M.; Christensen-Dalsgaard, J.; De Mauro, M.P.; Dziembowski, W.A.; Eff Darwich, A.; Gough, D.O.; Haber, D.A.; Hoeksema, J.T.; Howe, R.; Korzennik, S.G.; Kosovichev, A.G.; Larsen, R.M.; Pijpers, F.P.; Scherrer, P.H.; Sekii, T.; Tarbell, T.D.; Title, A.M.; Thompson, M.J.; Toomre, J. Helioseismic Studies of Differential Rotation in the Solar Envelope by the Solar Oscillations Investigation Using the Michelson Doppler Imager (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1998. — September (vol. 505). — P. 390—417. — doi:10.1086/306146. — Bibcode: 1998ApJ...505..390S.
  9. ↑ Antia, H.M.; Chitre, S.M.; Gough, D.O. Temporal variations in the Sun's rotational kinetic energy (англ.) // Astronomy and Astrophysics : journal. — 2008. — January (vol. 477). — P. 657—663. — doi:10.1051/0004-6361:20078209. — Bibcode: 2008A&A...477..657A.
  10. ↑ Fivian, M.D.; Hudson, H.S.; Lin, R.P.; Zahid, H.J. A Large Excess in Apparent Solar Oblateness Due to Surface Magnetism (англ.) // Science : journal. — 2008. — October (vol. 322). — P. 560—562. — doi:10.1126/science.1160863. — Bibcode: 2008Sci...322..560F.
  11. ↑ Kuhn, J.R.; Bush, R.; Emilio, M.; Scholl, I.F. The Precise Solar Shape and Its Variability (англ.) // Science. — 2012. — September (vol. 337). — P. 1638—1640. — doi:10.1126/science.1223231. — Bibcode: 2012Sci...337.1638K.
  12. ↑ Shapiro, I.T.; Counselman III, C.C.; King, R.W. Verification of the principle of equivalence for massive bodies (англ.) // Physical Review Letters : journal. — 1976. — March (vol. 36). — P. 555—558. — doi:10.1103/PhysRevLett.36.555. — Bibcode: 1976PhRvL..36..555S.
  13. ↑ Gough, D.O. Seismic constraints on the solar neutrino problem (англ.) // Annals of the New York Academy of Sciences[англ.] : journal. — 1991. — Vol. 647. — P. 199—217. — doi:10.1111/j.1749-6632.1991.tb32171.x. — Bibcode: 1991NYASA.647..199G.
  14. ↑ Bahcall, J.N.; Pinsonneault, M.H.; Basu, S.; Christensen-Dalsgaard, J. Are Standard Solar Models Reliable? (англ.) // Physical Review Letters : journal. — 1997. — January (vol. 78, no. 2). — P. 171—174. — doi:10.1103/PhysRevLett.78.171. — Bibcode: 1997PhRvL..78..171B. — arXiv:astro-ph/9610250.
  15. ↑ Gough, D.O. Helioseismology and solar neutrinos // Nuclear Physics B Proc. Suppl.. — 1999. — Май (т. 77). — С. 81—88. — doi:10.1016/S0920-5632(99)00401-6. — Bibcode: 1999NuPhS..77...81G.
  16. ↑ 1 2 Thompson, M.J.; Christensen-Dalsgaard, J.; Miesch, M.S.; Toomre, J. The Internal Rotation of the Sun (англ.) // Annual Review of Astronomy & Astrophysics[англ.] : journal. — 2003. — Vol. 41, no. 1. — P. 599—643. — doi:10.1146/annurev.astro.41.011802.094848. — Bibcode: 2003ARA&A..41..599T.
  17. ↑ Ossendrijver, M. The solar dynamo (англ.) // The Astronomy and Astrophysics Review[англ.] : journal. — 2003. — Vol. 11, no. 4. — P. 287—367. — doi:10.1007/s00159-003-0019-3. — Bibcode: 2003A&ARv..11..287O.
  18. ↑ Spiegel, E.A.; Zahn, J.-P. The solar tachocline (англ.) // Astronomy and Astrophysics : journal. — 1992. — November (vol. 265). — P. 106—114. — Bibcode: 1992A&A...265..106S.
  19. ↑ Gough, D.O.; McIntyre, M.E. Inevitability of a magnetic field in the Sun's radiative interior (англ.) // Nature : journal. — 1998. — August (vol. 394). — P. 755—757. — doi:10.1038/29472. — Bibcode: 1998Natur.394..755G.
  20. ↑ Vorontsov, S.V.; Christensen-Dalsgaard, J.; Schou, J.; Strakhov, V.N.; Thompson, M.J. Helioseismic Measurement of Solar Torsional Oscillations (англ.) // Science : journal. — 2002. — April (vol. 296, no. 5565). — P. 101—103. — doi:10.1126/science.1069190. — Bibcode: 2002Sci...296..101V. — PMID 11935019.
  21. ↑ Howard, R.; Labonte, B.J. The sun is observed to be a torsional oscillator with a period of 11 years (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1980. — July (vol. 239). — P. L33—L36. — doi:10.1086/183286. — Bibcode: 1980ApJ...239L..33H.
  22. ↑ 1 2 Braun, D.C.; Lindsey, C. Seismic Imaging of the Far Hemisphere of the Sun (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2001. — October (vol. 560, no. 2). — P. L189—L192. — doi:10.1086/324323. — Bibcode: 2001ApJ...560L.189B.
  23. ↑ Lindsey, C.; Braun, D.C. Helioseismic imaging of sunspots at their antipodes (англ.) // Solar Physics[англ.] : journal. — 1990. — March (vol. 126, no. 1). — P. 101—115. — doi:10.1007/BF00158301. — Bibcode: 1990SoPh..126..101L.
  24. ↑ Rabello-Soares, M.C.; Korzennik, S.G.; Schou, J. SOHO 10/GONG 2000 Workshop: Helio- and Asteroseismology at the Dawn of the Millennium (англ.) // In: Proceedings of the SOHO 10/GONG 2000 Workshop: Helio- and asteroseismology at the dawn of the millennium : journal. — 2001. — January (vol. 464). — P. 129—136. — Bibcode: 2001ESASP.464..129R.
  25. ↑ Elsworth, Y.P; Howe, R.; Isaak, G.R.; McLeod, C.,P.; New, R. Low-l p-mode solar eigenfrequency measurements from the Birmingham Network (англ.) // Monthly Notices of the Royal Astronomical Society : journal. — Oxford University Press, 1991. — July (vol. 251). — P. 7P—9P. — doi:10.1093/mnras/251.1.7P. — Bibcode: 1991MNRAS.251P...7E.
  26. ↑ Garcia, R.A.; Regulo, C.; Turck-Chieze, S.; Bertello, L.; Kosovichev, A.G.; Brun, A.S.; Couvidat, S.; Henney, C.J.; Lazrek, M.; Ulrich, R.K.; Varadi, F. Low-Degree Low-Order Solar p Modes As Seen By GOLF On board SOHO (англ.) // Solar Physics[англ.]. — 2001. — May (vol. 20). — P. 361—379. — doi:10.1023/A:1010344721148. — Bibcode: 2001SoPh..200..361G.
  27. ↑ Detection of individual normal modes of oscillation of the Sun in the period range from 2 hr to 10 min in solar diameter studies | SpringerLink (недоступная ссылка)
  28. ↑ Garcia, R.A.; Turck-Chieze, S.; Jimenez-Reyes, S.J.; Ballot, J.; Palle, P.L.; Eff-Darwich, A.; Mathur, S.; Provost, J. Tracking Solar Gravity Modes: The Dynamics of the Solar Core (англ.) // Science : journal. — 2007. — June (vol. 316, no. 5831). — P. 1591—. — doi:10.1126/science.1140598. — Bibcode: 2007Sci...316.1591G. — PMID 17478682.
  29. ↑ T.; Appourchaux; Belkacem, K.; Broomhall, A. M.; Chaplin, W. J.; Gough, D. O.; Houdek, G.; Provost, J.; Baudin, F.; Boumier, P.; Elsworth, Y.[англ.]; García, R. A.; Andersen, B.; Finsterle, W.; Fröhlich, C.; Gabriel, A.; Grec, G.; Jiménez, A.; Kosovichev, A.; Sekii, T.; Toutain, T.; Turck-Chièze, S. The quest for the solar g modes (англ.) // The Astronomy and Astrophysics Review[англ.] : journal. — 2009. — October (vol. 0910). — P. 848. — doi:10.1007/s00159-009-0027-z. — Bibcode: 2010A&ARv..18..197A. — arXiv:0910.0848.
  30. ↑ Gough, D.O. Astrophysical fluid dynamics, (ed. J-P. Zahn & J. Zinn-Justin, North-Holland, Amsterdam) (англ.) // Astrophysical fluid dynamics, (ed. J-P. Zahn & J. Zinn-Justin, North-Holland, Amsterdam) : journal. — 1993. — Vol. Les Houches Session XLVII. — P. 399—560. — Bibcode: 1993afd..conf..399G.
  31. ↑ Corbard, T.; Thompson, M.J. The subsurface radial gradient of solar angular velocity from MDI f-mode observations (англ.) // Solar Physics[англ.] : journal. — 2002. — February (vol. 205, no. 2). — P. 211—229. — doi:10.1023/A:1014224523374. — Bibcode: 2002SoPh..205..211C. — arXiv:astro-ph/0110361.
  32. ↑ Rhodes, Jr. E. J.; Kosovichev, A. G.; Schou, J.; et al. (1997), "Measurements of Frequencies of Solar Oscillations from the MDI Mediu-l Program", Solar Physics, 175: 287, Bibcode:1997SoPh..175..287R {{citation}}: Явное указание et al. в: |first3= (справка)
  33. ↑ 1 2 Christensen-Dalsgaard, J., 2003, Lecture Notes on Stellar Oscillations. Fifth Edition Архивная копия от 24 марта 2021 на Wayback Machine, lecture notes, University of Aarhus. Retrieved November 2009.
  34. ↑ Dziembowski, W.; Fiorentini, G.; Ricci, B.; Sienkiewicz, R. Helioseismology and the solar age (англ.) // Astronomy and Astrophysics : journal. — 1999. — Vol. 343. — P. 990—996. — Bibcode: 1999A&A...343..990D. — arXiv:astro-ph/9809361.
  35. ↑ Gough, D. Lessons Learned From Solar Oscillations // Astrophysical Ages and Times Scales / T.von Hippel, C. Simpson and N.Manset. — 2001. — Т. 245. — С. 31—43. — Bibcode: 2001ASPC..245...31G.
  36. ↑ Bonanno, A.; Schlattl, H.; Paternò, L. The age of the Sun and the relativistic corrections in the EOS (англ.) // Astronomy and Astrophysics : journal. — 2002. — Vol. 390, no. 3. — P. 1115—1118. — doi:10.1051/0004-6361:20020749. — Bibcode: 2002A&A...390.1115B. — arXiv:astro-ph/0204331.
  37. ↑ Houdek, G.; Gough, D. On the seismic age and heavy-element abundance of the Sun (англ.) // Mon. Not. R. Ast. Soc. : journal. — 2011. — Vol. 418. — P. 1217—1230. — doi:10.1111/j.1365-2966.2011.19572.x. — Bibcode: 2011MNRAS.418.1217H.
  38. ↑ Guenther, D.B. Age of the sun (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1989. — April (vol. 339). — P. 1156—1159. — doi:10.1086/167370. — Bibcode: 1989ApJ...339.1156G.
  39. ↑ Lindsey, C.; Braun, D.C.; Jefferies, S.M. "Local Helioseismology of Subsurface Structure" in "GONG 1992. Seismic Investigation of the Sun and Stars" (англ.) // GONG 1992. Seismic Investigation of the Sun and Stars. Proceedings of a Conference held in Boulder : journal / T.M. Brown. — 1993. — January (vol. 42). — P. 81—84. — ISBN 0-937707-61-9. — Bibcode: 1993ASPC...42...81L.
  40. ↑ Duvall, Jr.; T.L. "Recent Results and Theoretical Advances in Local Helioseismology" in "Structure and Dynamics of the Interior of the Sun and Sun-like Stars" (англ.) // Structure and Dynamics of the Interior of the Sun and Sun-like Stars SOHO 6/GONG 98 Workshop Abstract : journal / S. Korzennik. — 1998. — Vol. 418. — P. 581—585. — Bibcode: 1998ESASP.418..581D.
  41. ↑ Braun, D.C.; Duvall, Jr., T.L.; Labonte, B.J. Acoustic absorption by sunspots (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1987. — August (vol. 319). — P. L27—L31. — doi:10.1086/184949. — Bibcode: 1987ApJ...319L..27B.
  42. ↑ Hill, F. Rings and trumpets - Three-dimensional power spectra of solar oscillations (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1988. — October (vol. 333). — P. 996—1013. — doi:10.1086/166807. — Bibcode: 1988ApJ...333..996H.
  43. ↑ Basu, S.; Antia, H.M.; Bogart, R.S. Ring-Diagram Analysis of the Structure of Solar Active Regions (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2004. — August (vol. 610, no. 2). — P. 1157—1168. — doi:10.1086/421843. — Bibcode: 2004ApJ...610.1157B.
  44. ↑ Duvall, Jr., T.L.; Jefferies, S.M.; Harvey, J.W.; Pomerantz, M.A. Time-distance helioseismology (англ.) // Nature. — 1993. — April (vol. 362, no. 6419). — P. 430—432. — doi:10.1038/362430a0. — Bibcode: 1993Natur.362..430D.
  45. ↑ Jensen, J.M., 2003, Time-distance: what does it tell us?, in Local and Global Helioseismology: The Present and Future, (Ed.) Sawaya-Lacoste, H., Proceedings of SOHO 12/GONG+ 2002, 27 October - 1 November 2002, Big Bear Lake, California, U.S.A., vol. SP-517 of ESA Conference Proceedings, pp. 61–70, ESA Publications Division, Noordwijk
  46. ↑ Donea, A.-C.; Braun, D.C.; Lindsey, C. Seismic Images of a Solar Flare (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1999. — March (vol. 513, no. 2). — P. L143—L146. — doi:10.1086/311915. — Bibcode: 1999ApJ...513L.143D.
  47. ↑ Braun, D.C.; Fan, Y. Helioseismic Measurements of the Subsurface Meridional Flow (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1998. — November (vol. 508, no. 1). — P. L105—L108. — doi:10.1086/311727. — Bibcode: 1998ApJ...508L.105B.
  48. ↑ Braun, D.C.; Lindsey, C. Helioseismic Images of an Active Region Complex (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1999. — March (vol. 513, no. 1). — P. L79—L82. — doi:10.1086/311897. — Bibcode: 1999ApJ...513L..79B.
  49. ↑ 1 2 Woodard, M.F. Solar Subsurface Flow Inferred Directly from Frequency-Wavenumber Correlations in the Seismic Velocity Field (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2002. — January (vol. 565, no. 1). — P. 634—639. — doi:10.1086/324546. — Bibcode: 2002ApJ...565..634W.

Ссылки

[править | править код]
Источник — https://ru.wikipedia.org/w/index.php?title=Гелиосейсмология&oldid=139111636