Задача Кобона о треугольниках ({g;gcg TkQkug k mjyrikl,untg])
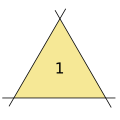
Как много неперекрывающихся треугольников могут быть образованы конфигурацией k прямых?

Зада́ча Кобо́на о треуго́льниках — нерешённая задача комбинаторной геометрии, сформулированная Кодзабуро Фудзмурой (яп. 藤村幸三郎 фудзимура ко:дзабуро:), известным также как Кобон. В задаче спрашивается, каково максимальное число N(k) неперекрывающихся треугольников, стороны которых принадлежат конфигурации k прямых. Вариант задачи рассматривается в проективной плоскости, а не в евклидовой плоскости, и в этом случае требуется, чтобы треугольники не пересекались другими прямыми конфигурации[1].
Верхние границы
[править | править код]Сабуро Тамура доказал, что наибольшее целое, не превосходящее k(k − 2)/3, даёт верхнюю границу максимального числа неперекрывающихся треугольников, получаемых из k прямых[2]. В 2007 году Иоганес Бадер и Жиль Клеман (нем. Johannes Bader, фр. Gilles Clément) нашли более сильную границу, доказав, что верхняя граница Тамуры не может быть достигнута для любого k, сравнимого с 0 или 2 по модулю 6[3]. Поэтому максимальное число треугольников на единицу меньше границы Тамура для этих случаев. Совершенные решения (решение задачи Кобона, дающие максимальное число треугольников) известны для k = 3, 4, 5, 6, 7, 8, 9, 13, 15 и 17[4]. Для k = 10, 11 и 12 наилучшие известные решения на единицу меньше верхней границы.
Если дано совершенное решение с k0 прямыми, другие решения задачи Кобона о треугольниках могут быть найдены для всех значений ki, где
при помощи процедуры Д. Форжа и Дж. Л. Рамиреза Альфонсина[1][5]. Например, решение для k0 = 3 приводит к максимальному числу неперекрывающихся треугольников для k = 3, 5, 9, 17, 33, 65, …
| k | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | OEIS |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Верхняя граница Тамуры для N(k) | 1 | 2 | 5 | 8 | 11 | 16 | 21 | 26 | 33 | 40 | 47 | 56 | 65 | 74 | 85 | 96 | 107 | 120 | 133 | [6] |
| Верхняя граница Клемана и Бадера | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 26 | 33 | 39 | 47 | 55 | 65 | 74 | 85 | 95 | 107 | 119 | 133 | — |
| Лучшие известные решения | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 25 | 32 | 38 | 47 | 53 | 65 | 72 | 85 | 93 | 104 | 115 | 130 | [7] |
Примеры
[править | править код]-
3 прямых образуют треугольник
-
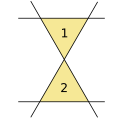
4 прямых
-
5 прямых
-
6 прямых
-
7 прямых
См. также
[править | править код]Примечания
[править | править код]- ↑ 1 2 Forge, Ramírez Alfonsín, 1998, p. 155–161.
- ↑ Weisstein, Eric W. Kobon Triangle (англ.) на сайте Wolfram MathWorld.
- ↑ G. Clément and J. Bader. Tighter. Upper Bound for the Number of Kobon Triangles. Draft Version (2007). Дата обращения: 10 марта 2016. Архивировано из оригинала 11 ноября 2017 года.
- ↑ Ed Pegg Jr. on Math Games Архивная копия от 11 марта 2016 на Wayback Machine.
- ↑ Matlab code illustrating the procedure of D. Forge and J. L. Ramirez Alfonsin Архивная копия от 8 марта 2021 на Wayback Machine. Retrieved on 9 May 2012.
- ↑ Последовательность A032765 в OEIS.
- ↑ Последовательность A006066 в OEIS.
Литература
[править | править код]- Forge D., Ramírez Alfonsín J. L. . Straight line arrangements in the real projective plane // Discrete and Computational Geometry, 1998, 20 (2). — P. 155—161. — doi:10.1007/PL00009373.
Ссылки
[править | править код]- Johannes Bader, "Kobon Triangles"
Для улучшения этой статьи желательно:
|