Группа кубика Рубика (Ijrhhg trQntg JrQntg)

Основная статья: Математика кубика Рубика

Группа кубика Рубика
Названо в честь	кубик Рубика
Изучается в	теория групп
Порядок группы	4,325200327449E+19
Медиафайлы на Викискладе

Развёртка кубика Рубика. Каждому из поворотов граней соответствует элемент группы S₄₈.

Гру́ппа ку́бика Ру́бика — подгруппа симметрической группы S₄₈, элементы которой соответствуют преобразованиям кубика Рубика. Под преобразованием подразумевается эффект поворота любой из граней или последовательности поворотов граней.

Определение

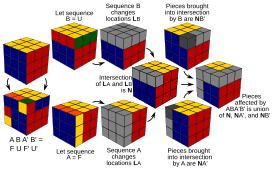
Каждый из поворотов граней кубика Рубика может рассматриваться как элемент симметрической группы множества 48 этикеток кубика Рубика, не являющихся центрами граней. Пометим центры граней буквами $\{L,F,R,B,U,D\}$ (left, front, right, back, up, down; левая, передняя, правая, задняя, верхняя, нижняя; см. рисунок), а остальные этикетки — числами от 1 до 48. Теперь поворотам соответствующих граней на 90° по часовой стрелке можно сопоставить элементы симметрической группы $S_{48}$:

$L=(1,3,8,6)(2,5,7,4)(33,9,41,32)(36,12,44,29)(38,14,46,27)$

$F=(9,11,16,14)(10,13,15,12)(38,17,43,8)(39,20,42,5)(40,22,41,3)$

$R=(17,19,24,22)(18,21,23,20)(48,16,40,25)(45,13,37,28)(43,11,35,30)$

$B=(25,27,32,30)(26,29,31,28)(19,33,6,48)(21,34,4,47)(24,35,1,46)$

$U=(33,35,40,38)(34,37,39,36)(25,17,9,1)(26,18,10,2)(27,19,11,3)$

$D=(41,43,48,46)(42,45,47,44)(6,14,22,30)(7,15,23,31)(8,16,24,32)$

Тогда группа кубика Рубика $G$ определяется как подгруппа $S_{48}$, порождаемая поворотами шести граней на 90°:

$G=\langle L,F,R,B,U,D\rangle$

Свойства

Порядок группы $G$ равен

$|G|={\dfrac {8!\cdot 12!\cdot 3^{8}\cdot 2^{12}}{3\cdot 2\cdot 2}}=43\ 252\ 003\ 274\ 489\ 856\ 000=2^{27}\cdot 3^{14}\cdot 5^{3}\cdot 7^{2}\cdot 11.$

Пусть $K_{f}$ — граф Кэли группы $G$ с 18 образующими, которые соответствуют 18 ходам метрики FTM.

Каждая из $\approx 4{,}32\cdot 10^{19}$ конфигураций может быть решена не более чем за 20 ходов FTM. Другими словами, эксцентриситет вершины графа $K_{f}$, соответствующей «собранному» состоянию головоломки, равен 20.

Диаметр графа $K_{f}$ также равен 20.

Наибольший порядок элемента в $G$ равен 1260. Например, последовательность ходов $(R\ U^{2}\ D^{\prime }\ B\ D^{\prime })$ необходимо повторить 1260 раз, прежде чем кубик Рубика вернётся в исходное состояние.

$G$ не является абелевой группой, так как, например, $FR\neq RF$. Другими словами, не все пары элементов коммутируют.

Подгруппы

Каждая группа, порядок которой не превышает 12, изоморфна некоторой подгруппе группы кубика Рубика. Каждая неабелева группа, порядок которой не превышает 24, также изоморфна некоторой подгруппе группы кубика Рубика. Группы $C_{13}$ (циклическая группа порядка 13) и $D_{26}$ (диэдральная группа порядка 26) не изоморфны никаким подгруппам группы кубика Рубика.

Центр группы

Центр группы состоит из элементов, коммутирующих с каждым элементом группы. Центр группы кубика Рубика состоит из двух элементов: тождественное преобразование и суперфлип.

Циклические подгруппы

В июле 1981 года Jesper C. Gerved и Torben Maack Bisgaard доказали, что группа кубика Рубика содержит элементы 73 различных порядков от 1 до 1260, и нашли число элементов каждого возможного порядка.

Порядок элемента	Последовательность поворотов граней
4	$F$
6	$R^{2}U^{2}$
63	$RU^{-1}$
105	$RU$
1260	$RU^{2}D^{-1}BD^{-1}$

Группа кубика Рубика содержит циклические подгруппы порядков

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15, 16, 18, 20, 21, 22, 24, 28, 30, 33, 35, 36, 40, 42, 44, 45, 48, 55, 56, 60, 63, 66, 70, 72, 77, 80, 84, 90, 99, 105, 110, 112, 120, 126, 132, 140, 144, 154, 165, 168, 180, 198, 210, 231, 240, 252, 280, 315, 330, 336, 360, 420, 462, 495, 504, 630, 720, 840, 990, 1260.

Лишь один элемент (единичный элемент группы) имеет порядок 1; второй наиболее редкий порядок — 11 (44 590 694 400 элементов); около 10,6 % всех элементов (4 601 524 692 892 926 000) имеют порядок 60.

В таблице приведены примеры последовательностей поворотов граней, соответствующих элементам некоторых порядков.

Группа квадратов

Группа квадратов (square group, squares group) — подгруппа группы $G$, порождаемая поворотами граней на 180°:

$G_{sq}=\langle L^{2},F^{2},R^{2},B^{2},U^{2},D^{2}\rangle$

Порядок группы квадратов равен 663 552.

Группа квадратов используется в алгоритме Тистлетуэйта, с помощью которого удалось доказать достаточность 45 ходов для сборки кубика Рубика.

Супергруппа кубика Рубика

Этикетки, находящиеся в центрах граней кубика Рубика, не перемещаются, но поворачиваются. На обычном кубике Рубика ориентация центров граней невидима.

Группа всех преобразований кубика Рубика с видимыми ориентациями центров граней называется супергруппой кубика Рубика. Она в ${\dfrac {4^{6}}{2}}=2048$ раз больше группы $G$.

Гамильтонов цикл на графе Кэли

На графе Кэли $K_{q}$ группы $G$ с 12 образующими, которые соответствуют ходам метрики QTM, существует гамильтонов цикл. Найденный цикл использует повороты только 5 из 6 граней.

Существует соответствующая гипотеза Ловаса для произвольного графа Кэли.

См. также

• Гамильтонов граф
• Граф Кэли
• Нормальная подгруппа
• Перестановка
• Теория групп

Литература

• Joyner, David. Adventures in group theory: Rubik's Cube, Merlin's machine, and Other Mathematical Toys (англ.). — Baltimore: Johns Hopkins University Press, 2002. — ISBN 0-8018-6947-1.
• Савин А. П. Математические миниатюры / Художник Е. Шабельник. — М.: Детская литература, 1991. — С. 79—81. — 127 с. — (Знай и умей). — ISBN 5-08-000596-3.
• W. D. Joyner. Mathematics of the Rubik's Cube  (неопр.) (1996). Дата обращения: 5 декабря 2015. Архивировано 20 февраля 2016 года.

Ссылки

• W. D. Joyner. Lecture notes on the mathematics of the Rubik's cube (англ.). Дата обращения: 22 июля 2013. Архивировано 5 сентября 2013 года.
• Janet Chen. Group Theory and the Rubik's Cube  (неопр.). Дата обращения: 28 марта 2022. Архивировано 30 сентября 2019 года.