Граф Эллингема — Хортона (Ijgs |llnuiybg — }kjmkug)
| Графы Эллингема — Хортона | |
|---|---|
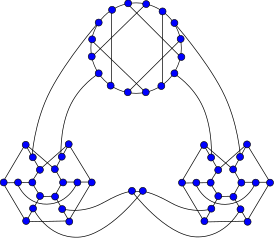 54-граф Эллингема — Хортона. | |
| Назван в честь | Джозеф Хортон и Марк Эллингем |
| Вершин |
54 (54-граф) 78 (78-граф) |
| Рёбер |
81 (54-граф) 117 (78-граф) |
| Радиус |
9 (54-граф) 7 (78-граф) |
| Диаметр |
10 (54-граф) 13 (78-граф) |
| Обхват | 6 (оба) |
| Автоморфизмы |
32 (54-граф) 16 (78-граф) |
| Хроматическое число | 2 (оба) |
| Хроматический индекс | 3 (оба) |
| Свойства |
кубические (оба) двудольные (оба) регулярные (оба) |
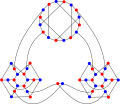
Графы Эллингема — Хортона — два 3-регулярных графа с 54 и 78 вершинами — 54-граф Эллингема — Хортона и 78-граф Эллингема — Хортона[1]. Графы названы именами Джозефа Хортона и Марка Эллингема, которые их открыли. Эти два графа дают контрпримеры гипотезе Уильяма Татта о том, что каждый кубический 3-связный двудольный граф является гамильтоновым[2].
Первым контрпримером гипотезы Татта был граф Хортона, который опубликовали Бодни и Мёрти[3]. После графа Хортона было найдено несколько меньших контрпримеров гипотезе Татта. Среди них находятся 92-вершинный граф Хортона[4], 78-вершинный граф Овенса[5] и два графа Эллингема — Хортона.
Первый граф Эллингема — Хортона опубликовал Эллингем и он имеет порядок 78[6]. В то время граф был наименьшим известным контрпримером гипотезе Татта. Второй граф Эллингема — Хортона опубликовали Эллингем и Хортон и он имеет порядок 54[7]. В 1989 был открыт на настоящее время наименьший негамильтонов 3-связный кубический двудольный граф Жоржа, содержащий 50 вершин[8].
Галерея
[править | править код]-
Хроматическое число 54-графа Эллингема — Хортона равно 2.
-
Хроматический индекс 54-графа Эллингема — Хортона равен 3.
-
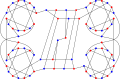
Хроматическое число 78-графа Эллингема — Хортона равно 2.
-
Хроматический индекс 78-графа Эллингема — Хортона равен 3.
Примечания
[править | править код]- ↑ Weisstein, Eric W. Tutte Conjecture (англ.) на сайте Wolfram MathWorld.
- ↑ Tutte, 1971, с. 203–208.
- ↑ Bondy, Murty, 1976, с. 240.
- ↑ Horton, 1982, с. 35–41.
- ↑ Owens, 1983, с. 327–330.
- ↑ Ellingham, 1981.
- ↑ Ellingham, Horton, 1983, с. 350–353.
- ↑ Georges, 1989, с. 121–124.
Литература
[править | править код]- Tutte W. T. On the 2-factors of bicubic graphs // Discrete Mathematics. — 1971. — Т. 1, вып. 2. — С. 203—208. — doi:10.1016/0012-365X(71)90027-6.
- Bondy J. A., Murty U. S. R. Graph Theory with Applications. — New York: North Holland, 1976. — С. 240. — ISBN 0-444-19451-7. Архивная копия от 13 апреля 2010 на Wayback Machine
- Horton J. D. On two-factors of bipartite regular graphs // Discrete Mathematics. — 1982. — Т. 41, вып. 1. — С. 35—41. — doi:10.1016/0012-365X(82)90079-6.
- Owens P. J. Bipartite cubic graphs and a shortness exponent // Discrete Mathematics. — 1983. — Т. 44, вып. 3. — С. 327—330. — doi:10.1016/0012-365X(83)90201-7.
- Ellingham M. N. Non-Hamiltonian 3-connected cubic partite graphs. — Melbourne: Dept. of Math., Univ. Melbourne, 1981. — (Research Report 28).
- Ellingham M. N., Horton J. D. Non-Hamiltonian 3-connected cubic bipartite graphs // Journal of Combinatorial Theory, Series B. — 1983. — Т. 34, вып. 3. — С. 350—353. — doi:10.1016/0095-8956(83)90046-1.
- Georges J. P. Non-hamiltonian bicubic graphs // Journal of Combinatorial Theory, Series B. — 1989. — Т. 46, вып. 1. — С. 121—124. — doi:10.1016/0095-8956(89)90012-9.
Для улучшения этой статьи желательно:
|