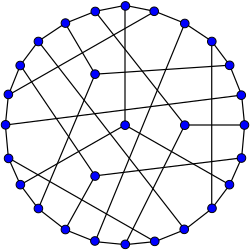
Граф Коксетера (Ijgs Tktvymyjg)

Эта статья — об определённом 3-регулярном графе. О графах, описывающих группы Коксетера, см. Диаграммы Коксетера — Дынкина.

Граф Коксетера
Вершин	28
Рёбер	42
Радиус	4
Диаметр	4
Обхват	7
Автоморфизмы	336 (PGL2(7))
Хроматическое число	3
Хроматический индекс	3
Свойства	кубический симметричный дистанционно-транзитивный дистанционно-регулярный гипогамильтонов
Медиафайлы на Викискладе

Граф Коксетера — 3-регулярный граф с 28 вершинами и 42 рёбрам Все кубические дистанционно-регулярные графы известны, граф Коксетера — один из 13-ти таких графов.

Свойства

Хроматическое число графа равно 3, хроматический индекс равен 3, радиус равен 4, диаметр — 4, а обхват — 7. Граф является также вершинно 3-связным и рёберно 3-связным.

Граф Коксетера является гипогамильтоновым — сам по себе он не содержит гамильтоновых циклов, но удаление любой вершины делает его гамильтоновым. Число прямолинейных скрещиваний графа Коксетера равно 11 и это минимальный известный кубический граф с таким числом скрещиваний, хотя графы с 26 вершинами и числом скрещиваний 11 существовать могут.

Граф Коксетера можно построить из несколько меньшего дистанционно-регулярного графа Хивуда путём создания вершины для каждого 6-цикла в графе Хивуда и ребра для каждой несвязной пары 6-циклов.

Алгебраические свойства

Группа автоморфизмов графа Коксетера — это группа порядка 336. Она действует транзитивно на вершины и рёбра графа, поэтому граф Фостера является симметричным. Граф имеет автоморфизмы, которые переводят любую вершину в любую другую и любое ребро в любое другое ребро. В списке Фостера граф Коксетера, указанный как F28A, является единственным кубическим симметричным графом с 28 вершинами.

Граф Коксетера однозначно определяется по его спектру, множеству собственных значений матрицы смежности графа.

Как конечный связный вершинно-транзитивный граф, не содержащий гамильтонов цикл, граф Коксетера является контрпримером варианта гипотезы Лаваша, но каноническая формулировка гипотезы требует наличия гамильтонова цикла.

Известно только пять вершинно-транзитивных графов без гамильтоновых циклов — полный граф K₂, граф Петерсена, граф Коксетера и два графа, полученные из графов Петерсена и Коксетера путём замены каждой вершины треугольником.

Характеристический многочлен графа Коксетера равен $(x-3)(x-2)^{8}(x+1)^{7}(x^{2}+2x-1)^{6}$. Граф является единственным графом с таким полиномом, что делает граф однозначно определяемым по его спектру.

Галерея

• 
  Граф, полученный удалением любого ребра из графа Коксетера является гамильтоново-связным.
• 
  Хроматическое число графа Коксетера равно 3.
• 
  Число прямолинейных скрещиваний графа Коксетера равно  11.