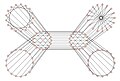
Граф Биггса — Смита (Ijgs >niivg — Vbnmg)
| Граф Биггса–Смита | |
|---|---|
 | |
| Вершин | 102 |
| Рёбер | 153 |
| Радиус | 7 |
| Диаметр | 7 |
| Обхват | 9 |
| Автоморфизмы | 2448 (PSL(2,17)) |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Свойства |
кубический
дистанционно-регулярный |
Граф Биггса — Смита — 3-регулярный граф с 102 вершинами и 153 рёбрами[1]. Назван в честь Биггса и Смита, описавших граф в 1971 году.[2]
Хроматическое число графа равно 3, хроматический индекс равен 3, радиус равен 7, диаметр — 7, а обхват — 9. Граф является также вершинно 3-связным и рёберно 3-связным.
Все кубические дистанционно-регулярные графы известны[3], граф Биггса — Смита — один из 13-ти таких графов.
Алгебраические свойства
[править | править код]Группа автоморфизмов графа Биггса — Смита — это группа порядка 2448[4], изоморфная группе проективной группе PSL(2,17). Она действует транзитивно на вершины и рёбра графа, поэтому граф Биггса — Смита является симметричным. Граф имеет автоморфизмы, которые переводят любую вершину в любую другую и любое ребро в любое другое ребро. В списке Фостера граф Биггса — Смита, указанный как F102A, является единственным симметричным графом с 102 вершинами[5].
Граф Биггса — Смита однозначно определяется по его спектру, множеству собственных значений матрицы смежности графа[6].
Характеристический многочлен графа Биггса — Смита равен:
- .
Галерея
[править | править код]-
Хроматическое число графа Биггса — Смита равно 3.
-
Хроматический индекс графа Биггса — Смита равен 3.
-
Альтернативное графическое представление графа Биггса — Смита.
-
Разложение графа Биггса — Смита на 6 множеств по 17 элементов в каждом.
Примечания
[править | править код]- ↑ Weisstein, Eric W. Biggs–Smith Graph (англ.) на сайте Wolfram MathWorld.
- ↑ Biggs, N. L., & Smith, D. H. (1971). On Trivalent Graphs. Bulletin of the London Mathematical Society, 3(2), 155–158. doi:10.1112/blms/3.2.155
- ↑ A. E. Brouwer, A. M. Cohen, A. Neumaier. Distance-Regular Graphs.. — New York: Springer-Verlag, 1989.
- ↑ Royle, G. F102A data (недоступная ссылка)
- ↑ M. Conder, P. Dobcsányi, «Trivalent Symmetric Graphs Up to 768 Vertices.» J. Combin. Math. Combin. Comput. 40, 41-63, 2002.
- ↑ E. R. van Dam and W. H. Haemers, Spectral Characterizations of Some Distance-Regular Graphs. J. Algebraic Combin. 15, pages 189—202, 2003
Литература
[править | править код]- On trivalent graphs, NL Biggs, DH Smith — Bulletin of the London Mathematical Society, 3 (1971) 155—158.