Бабочка (БПФ) (>gQkctg (>HS))

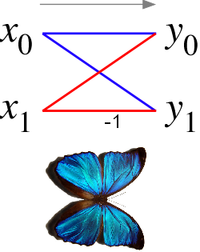
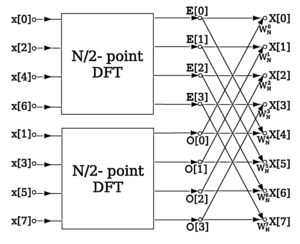
Диаграмма потока данных соединяет входы x (слева) с выходами y (справа) для «бабочки» алгоритма БПФ. Диаграмма напоминает бабочку (на рисунке приводится бабочка Морфо)

БПФ по основанию 2 с прореживанием по времени разбивает ДПФ размерности N на два ДПФ размерности *N/2* c последующим объединяющим шагом, состоящим из множественных операций "бабочка".

Бабочка — элементарный шаг в алгоритме Кули-Тюки (англ. Cooley–Tukey FFT) вычисления быстрого преобразования Фурье.

Время работы шага Бабочка определяет длительность вычисления преобразования Фурье.^[1]

В простейшем варианте (Radix-2 butterfly) является двухточечным преобразованием.

Формула для вычисления «Бабочки»:^[1]

$Y_{1}=X_{1}+X_{2}\cdot W$

$Y_{2}=X_{1}-X_{2}\cdot W$

Обозначения: $X_{1}$ , $X_{2}$ – исходные точки; $Y_{1}$ , $Y_{2}$ – точки результата, $W$ – комплексный коэффициент.

Для БПФ данных размером $2^{k}=N$ , требуется произвести $N\cdot \log _{2}N$ вычислений операции 2-Radix «Бабочка».^[1]^[2]^[3]

Иногда используются операции бабочка более высокого порядка: Radix-4, Radix-8. Radix-4 является примерно на 20% более эффективным для преобразования Фурье большого количества данных. Операция большего порядка чем 8 практически не используется из-за незначительных приростов производительности и трудностей в реализации (ресурсоемкости).^[4]^[5]

Сходная структура может применяться в реализациях алгоритма Витерби (операция ACS - Add-Compare-Select)^[6].

Примечания

↑ ¹ ² ³ Реализация целочисленного БПФ на процессорах с архитектурой ARM // Схемотехника №3 март 2001
↑ Л. Рабинер и Б. Гоулд "Теория и применение цифровой обработки сигналов".
↑ Архивированная копия (неопр.). Дата обращения: 29 декабря 2012. Архивировано из оригинала 14 августа 2003 года.
↑ http://www.ece.ucdavis.edu/~bbaas/281/slides/Handout.fft2.pdf Архивная копия от 6 декабря 2012 на Wayback Machine Higher Radices
↑ http://www.cmlab.csie.ntu.edu.tw/cml/dsp/training/coding/transform/fft.html Архивная копия от 30 апреля 2010 на Wayback Machine Radix-4 FFT Algorithm; Figure TC.3.9 Basic butterfly computation in a radix-4 FFT algorithm
↑ Implementing the Viterbi Algorithm in Today's Digital Communications Systems Архивная копия от 25 декабря 2012 на Wayback Machine // Design And Reuse (EETimes): "Viterbi ACS instructions are based on the Viterbi butterfly structure and symmetry. The structure is called “butterfly” due to its physical resemblance to the animal.", Figures 8-10

Ссылки

Chapter 12: The Fast Fourier Transform (The Scientist and Engineer's Guide to Digital Signal Processing, By Steven W. Smith); перевод

[pl01-1] ¹ ² ³ Реализация целочисленного БПФ на процессорах с архитектурой ARM // Схемотехника №3 март 2001

[2] Л. Рабинер и Б. Гоулд "Теория и применение цифровой обработки сигналов".

[3] Архивированная копия (неопр.). Дата обращения: 29 декабря 2012. Архивировано из оригинала 14 августа 2003 года.

[4] ttp://www.ece.ucdavis.edu/~bbaas/281/slides/Handout.fft2.pdf Архивная копия от 6 декабря 2012 на Wayback Machine Higher Radices

[5] ttp://www.cmlab.csie.ntu.edu.tw/cml/dsp/training/coding/transform/fft.html Архивная копия от 30 апреля 2010 на Wayback Machine Radix-4 FFT Algorithm; Figure TC.3.9 Basic butterfly computation in a radix-4 FFT algorithm

[6] Implementing the Viterbi Algorithm in Today's Digital Communications Systems Архивная копия от 25 декабря 2012 на Wayback Machine // Design And Reuse (EETimes): "Viterbi ACS instructions are based on the Viterbi butterfly structure and symmetry. The structure is called “butterfly” due to its physical resemblance to the animal.", Figures 8-10

[1]

[2]

[3]

[4]

[5]

[6]