Автомат Мура (Gfmkbgm Brjg)

Автомат Мура
Автомат Мура
Названо в честь	Эдвард Форест Мур
Первооткрыватель или изобретатель	Эдвард Форест Мур
	Медиафайлы на Викискладе

Автомат Мура (абстрактный автомат второго рода) в теории вычислений — конечный автомат, выходное значение сигнала в котором зависит лишь от текущего состояния данного автомата, и не зависит напрямую, в отличие от автомата Мили, от входных значений. Автомат Мура назван в честь описавшего его свойства Эдварда Ф. Мура, опубликовавшего исследования в 1956 году в издании «Gedanken-experiments on Sequential Machines»^[1].

Формальное определение

Автомат Мура может быть определён как кортеж из 6 элементов, включающий:

множество внутренних состояний S (внутренний алфавит);
начальное состояние s₀;
множество входных сигналов X (входной алфавит);
множество выходных сигналов Y (выходной алфавит)
функция переходов $\Phi :S\times X\rightarrow S$ .
функция вывода $\operatorname {G} :S\rightarrow Y$ .

Связь с автоматами Мили

Для любого автомата Мура существует эквивалентный ему автомат Мили: любой автомат Мура путём добавления ряда внутренних состояний может быть преобразован в автомат Мили. Обратное, строго говоря, неверно: дело в том, что сигнал на выходе автомата Мура зависит только от входного сигнала в предыдущие моменты времени, а выходной сигнал для автомата Мили может зависеть от входного сигнала и в текущий момент времени. Для автомата Мили можно в общем случае построить лишь автомат Мура, который ему почти эквивалентен: а именно его выход будет сдвинут во времени на 1^[2]. Если мы изменим определение автомата Мура, таким образом, что автомат будет выводить значение $\operatorname {G} (s)$ в конце транзакции $s\rightarrow s'$ , а не в начале, то такие автоматы будут полностью эквивалентны автоматам Мили.

Способы задания

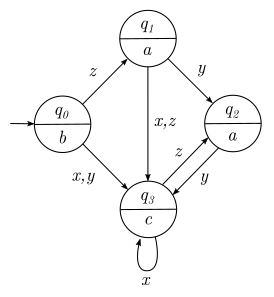
Диаграмма — изображённый на плоскости ориентированный граф, вершины которого взаимно однозначно соответствуют состояниям автомата, а дуги — входным символам.
Таблица переходов-выходов, в ячейках которой для каждой пары значений аргументов х(t), s(t) проставляются будущие внутренние состояния s(t+1). Значения выходных сигналов y(t) представляются в отдельном столбце.

Таблица переходов

	y₁	y₂	y₃	y₁	y₂	y₂	y₃
	s₁	s₂	s₃	s₄	s₅	s₆	s₇
$x_{1}$	s₅	s₄	s₅	s₃	s₄	s₂	s₅
$x_{2}$	s₇	s₁	s₄	s₂	s₁	s₃	s₄

См. также

JFLAP кроссплатформенная программа симулятор автоматов, машины Тьюринга, грамматик, рисует граф автомата
Автомат Мура в сравнении с автоматом Мили

Примечания

↑ Moore, Edward F. Gedanken-experiments on Sequential Machines (англ.) // Automata Studies,Annals of Mathematical Studies. — Princeton, N.J.: Princeton University Press, 1956. — No. 34. — P. 129—153.
↑ Edward A. Lee and Sanjit A. Seshia. Introduction to Embedded Systems (англ.). — Second Edition. — MIT Press, 2017. — P. 58. — ISBN 978-0-262-53381-2. Архивировано 30 марта 2018 года.

Литература

Karacuba A. A. Experimente mit Automaten (German) // Elektron. Inform.-verarb. Kybernetik, 11, 611—612 (1975). (нем.)
Карацуба А. А. Решение одной задачи из теории конечных автоматов // УМН, т. 15, № 3(93), с. 157—159 (1960). (рус.)
Карацуба А. А. Список научных трудов (рус.)
Karacuba A. A. Experimente mit Automaten (German) Elektron. Informationsverarb. Kybernetik, 11, 611—612 (1975). (англ.)
Moore E. F. Gedanken-experiments on Sequential Machines. Automata Studies, Annals of Mathematical Studies, 34, 129—153. Princeton University Press, Princeton, N.J.(1956). (англ.)

[gedanken-1] Moore, Edward F. Gedanken-experiments on Sequential Machines (англ.) // Automata Studies,Annals of Mathematical Studies. — Princeton, N.J.: Princeton University Press, 1956. — No. 34. — P. 129—153.

[2] Edward A. Lee and Sanjit A. Seshia. Introduction to Embedded Systems (англ.). — Second Edition. — MIT Press, 2017. — P. 58. — ISBN 978-0-262-53381-2. Архивировано 30 марта 2018 года.

[1]

[2]