MLAB (MLAB)

MLAB
Тип	математические расчёты
Разработчик	Civilized Software Inc.
Написана на	C, ассемблер, MLAB
Операционные системы	Microsoft Windows, Linux, Mac OS X
Первый выпуск	1985 (1985)
Аппаратные платформы	IA-32, x86-64
Состояние	активное
Лицензия	коммерческая
Сайт	civilized.com/mlabdesc.html
Медиафайлы на Викискладе

MLAB (от Modeling Laboratory ) — кроссплатформенная многопарадигменная вычислительная среда для математических расчётов с языком программирования четвертого поколения, разработанная в 1970-х годах в Национальном институте здравоохранения США (англ. National Institutes of Health). С 1985 года разработку ведёт Civilized Software, Inc.

Собственный язык программирования MLAB позволяет выполнять операции с матрицами, функциями и данными, реализовывать алгоритмы, а также поддерживает аппроксимацию кривых, дифференциальные уравнения, статистические функции и рисует графики.

MLAB предназначен для численных расчётов со специальными средствами для решения обыкновенных дифференциальных уравнений и подбора кривых (нелинейная регрессия). Он предоставляет более тридцати типов команд и более 450 встроенных функций из областей элементарной математики, трансцендентных функций, теории вероятностей и математической статистики, линейной алгебры, оптимизации, кластерного анализа, комбинаторики, ввода/вывода чисел и графики.

Присутствуют обычные низкоуровневые функции, такие как синус, косинус, логарифм и другие, а также более сложные функции математического анализа, такие как разложение по сингулярным числам, дискретное преобразование Фурье, решение систем дифференциальных уравнений, непараметрическое моделирование и ограниченная нелинейная оптимизация и многие другие. В это ПО включен большой набор статистических функций, в том числе наиболее распространённые прямые и обратные функции распределения, а также функции создания графиков, поддерживающие графическое отображение сложнейших функций.

Многие программные пакеты могут численно интегрировать обыкновенные дифференциальные уравнения, но MLAB — один из очень немногих, который также может настраивать их параметры и начальные условия. MLAB одинаково удобен при подборе кривой, когда корректировки являются линейными или, как в случае с большинством моделей дифференциальных уравнений, нелинейными.

MLAB широко используется в академических и научно-исследовательских институтах, а также на промышленных предприятиях.

История

MLAB был разработан в Национальном институте здравоохранения в конце 1970-х годов с совместно со Стэнфордской пабораторией искусственного интеллекта (англ. Stanford Artificial Intelligence Laboratory, SAIL) при Стэнфордском университете, для компьютеров PDP-10 производства Digital Equipment Corporation (DEC).

В 1985 году создатели MLAB основали компанию Civilized Software, Inc. и доработали MLAB в конце 1980-х и начале 1990-х годов за счет грантов на исследования в области инноваций для малого бизнеса.

Первыми использовали MLAB исследователи и практики в области биохимии, но его применение быстро распространилось на многие другие области. В настоящее время он также используется в образовании, в частности, при обучении линейной алгебре, численным методам математического анализа.

Теперь MLAB популярен среди ученых, занимающихся анализом и моделированием химической кинетики и сегментным моделированием в фармакологических (включая фармакокинетику) и физиологических исследованиях.

Синтакс языка программирования

Приложение MLAB построено на языке сценариев MLAB. Типичное использование приложения MLAB включает использование командного окна в качестве интерактивного математического вычислителя или выполнение текстовых файлов с программами на языке MLAB.

В MLAB существуют десятки команд и сотни функций. По сути, MLAB — это интерпретатор математического языка программирования высокого уровня с возможностью обработки (повторного запуска) файлов с текстом программы, называемых do-файлами.

MLAB может использовать символьные производные, когда значения производных необходимы во время подбора кривой или решения обыкновенных дифференциальных уравнений. Также в MLAB можно подобрать (или просто решить) модели, определяемые дифференциальными уравнениями, чтобы можно было обрабатывать химическую кинетику, физиологические и компартментальные модели.

Примеры

В MLAB можно определить функцию и построить её график следующим образом:

 function f(x) = a*cos(b*x)*exp(-k*x)
 a = 1; b=4; k =.5
 v=1:10!100
 m= points(f,v)
 draw m
 view

В результате получается простой график:

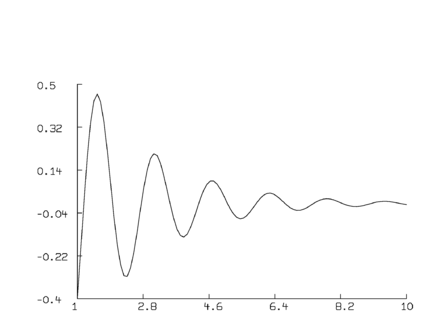
Обратите внимание, что 1:10!100 = 1:10:0,0909090909, то есть вертикальная шкала графике имеет диапазон значений от 1 до 10 с шагом 0,0909090909.

Также обратите внимание, что ф языке MLAB функция points(f,v) означают постолбцовую конкатенацию матрицы v с вектором-столбцом того же размера, состоящим из значений f, вычисленных по значениям из v.

Можно прочитать 110 значений данных из файла в матрицу из 2 столбцов следующим образом (результатом является матрица из 55 строк и 2 столбцов).

d = read("filename",55,2)

Взяв строки матрицы d как точки данных (x, y), с ошибкой в значениях y, где эти точки данных «моделируются» функцией f, определённой выше, можно оценить неизвестные параметры a, b, k следующим образом:

fit(a,b,k), f to d

Можно использовать оценочные веса для различных точек данных в d на основе функции оценки скользящей дисперсии ewt следующим образом:

fit(a,b,k), f to d with wt ewt(d)

Можно графически представить данные и «подгонку»:

delete w /* чтобы удалить предыдущий график */
draw d linetype none, pointtype circle
draw points(f,d col 1) color green
view

Можно посмотреть на символьную производную от f и изобразить её:

type f'x
draw points(f'x, d col 1) color red
view

См. также

• Сравнение программного обеспечения для численного анализа
• Список программного обеспечения для численного анализа

Литература

• Knott, G. D. Mlab — A mathematical modeling tool : [англ.] // Computer Programs in Biomedicine. — 1979. — Vol. 10, no. 3. — P. 271–280. — doi:10.1016/0010-468X(79)90075-8.
• MLAB: An Advanced System for Mathematical and Statistical Modeling / G. D. Knott // Modern Trends in Biothermokinetics : [англ.] / Ed. by S. Schuster et al.. — New York : Plenum Press, 1993. — P. 451–454. — ISBN 978-1-4615-2962-0. — doi:10.1007/978-1-4615-2962-0_70.

Ссылки

• civilized.com/mlabdesc.html (англ.) — официальный сайт MLAB
• MLAB-1 (англ.). Quora.